6. 巧算:$998÷998\frac{998}{999}+\frac{1}{1000}$。
答案:原式$=998÷\frac{998×999+998}{999}+\frac{1}{1000}=998÷\frac{998×(999+1)}{999}+\frac{1}{1000}=998×\frac{999}{998×1000}+\frac{1}{1000}=\frac{999}{1000}+\frac{1}{1000}=1$ 提示:根据数据特点,选择合适的方法计算。
解析:
原式$=998÷\frac{998×999 + 998}{999}+\frac{1}{1000}$
$=998÷\frac{998×(999 + 1)}{999}+\frac{1}{1000}$
$=998×\frac{999}{998×1000}+\frac{1}{1000}$
$=\frac{999}{1000}+\frac{1}{1000}$
$=1$
$=998÷\frac{998×(999 + 1)}{999}+\frac{1}{1000}$
$=998×\frac{999}{998×1000}+\frac{1}{1000}$
$=\frac{999}{1000}+\frac{1}{1000}$
$=1$
7. 某水果店店主用的秤缺斤少两,方华买 1000 克苹果,回家一称实际只有 900 克。于是就找到店主,店主用店里的秤又称了 100 克给他,并说:“现在你不吃亏了!”店主说的其实不对。请你算一算,方华还亏了多少克?
答案:实际质量:称出质量$=9:10$称出100克,实际只有$100×\frac{9}{10}=90$(克)$100-90=10$(克) 提示:1000克苹果,只称出了900克,这里的900克是实际质量,而1000克是店主的秤有问题导致的称出的不准确结果,说明实际质量和称出质量之比为$9:10$,现在称出100克,而实际质量只有$100×\frac{9}{10}=90$(克),$100-90=10$(克),所以方华还亏了10克。
解析:
实际质量与称出质量的比为$900:1000=9:10$。
店主称出100克,实际质量为$100×\frac{9}{10}=90$克。
方华应得100克,实际只得到90克,还亏了$100 - 90=10$克。
答:方华还亏了10克。
店主称出100克,实际质量为$100×\frac{9}{10}=90$克。
方华应得100克,实际只得到90克,还亏了$100 - 90=10$克。
答:方华还亏了10克。
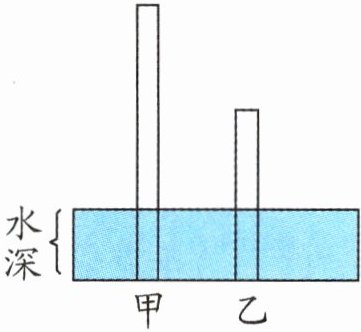
8. 如图,甲、乙两根木棒垂直插入水池中,两根木棒的长度和为 380 厘米,甲棒有$\frac{3}{4}$在水面上,乙棒有$\frac{4}{7}$在水面上,水深多少厘米?
]
]

答案:$(1-\frac{4}{7}):(1-\frac{3}{4})=12:7$$380×\frac{12}{12+7}=240$(厘米)$240×(1-\frac{3}{4})=60$(厘米) 提示:由于插入水池中的长度是相同的,即甲的$1-\frac{3}{4}=\frac{1}{4}$与乙的$1-\frac{4}{7}=\frac{3}{7}$相等,所以甲、乙长度的比是$\frac{3}{7}:\frac{1}{4}=12:7$。由此可以求出甲、乙的长度各占长度和的几分之几,进而求出水深。
解析:
甲棒在水下的部分占比为$1 - \frac{3}{4} = \frac{1}{4}$,乙棒在水下的部分占比为$1 - \frac{4}{7} = \frac{3}{7}$。
因为水深相同,所以甲棒长度$×\frac{1}{4} = $乙棒长度$×\frac{3}{7}$,则甲、乙两棒长度比为$\frac{3}{7}:\frac{1}{4} = 12:7$。
总份数为$12 + 7 = 19$,甲棒长度为$380×\frac{12}{19} = 240$厘米。
水深为$240×\frac{1}{4} = 60$厘米。
答:水深60厘米。
因为水深相同,所以甲棒长度$×\frac{1}{4} = $乙棒长度$×\frac{3}{7}$,则甲、乙两棒长度比为$\frac{3}{7}:\frac{1}{4} = 12:7$。
总份数为$12 + 7 = 19$,甲棒长度为$380×\frac{12}{19} = 240$厘米。
水深为$240×\frac{1}{4} = 60$厘米。
答:水深60厘米。
9. 甲、乙两人分别从 A、B 两地同时出发,相向而行,出发时他们的速度之比是$3:2$,他们相遇后,甲的速度提高了$\frac{1}{5}$,乙的速度提高了$\frac{3}{10}$。当甲到达 B 地时,乙离 A 地还有 14 千米,求 A、B 两地的距离。
答案:由于甲、乙两人出发时的速度之比是$3:2$,所以相遇时甲、乙两人走的路程之比是$3:2$。他们相遇后,甲的速度提高了$\frac{1}{5}$,乙的速度提高了$\frac{3}{10}$,此时甲、乙两人的速度之比是$[3×(1+\frac{1}{5})]:[2×(1+\frac{3}{10})]=18:13$。当甲到达B地时,乙离A地的距离占全部路程的$\frac{3}{5}-\frac{2}{5}÷18×13=\frac{14}{45}$,是14千米,因此A、B两地的距离是$14÷\frac{14}{45}=45$(千米)。 提示:把A、B两地之间的距离看作单位“1”,相遇前甲、乙速度比是$3:2$,在相同时间内所行路程的比等于速度的比,所以相遇时甲行了全程的$\frac{3}{5}$,乙行了全程的$\frac{2}{5}$,相遇后,甲、乙速度之比为$[3×(1+\frac{1}{5})]:[2×(1+\frac{3}{10})]=\frac{18}{5}:\frac{13}{5}=18:13$,当甲走完剩下的路程时,乙又走完全程的$\frac{2}{5}×\frac{13}{18}=\frac{13}{45}$,还剩全程的$\frac{3}{5}-\frac{13}{45}=\frac{14}{45}$,也就是14千米,根据已知一个数的几分之几是多少,求这个数,用除法解答。解答此题首先要明确:在相同时间内所行路程的比等于速度的比,关键是求出14千米占A、B两地间距离的几分之几。
解析:
设A、B两地的距离为单位“1”。
相遇时,甲、乙路程比等于速度比$3:2$,则相遇时甲行了全程的$\frac{3}{3+2}=\frac{3}{5}$,乙行了全程的$\frac{2}{3+2}=\frac{2}{5}$。
相遇后,甲的速度为$3×(1+\frac{1}{5})=\frac{18}{5}$,乙的速度为$2×(1+\frac{3}{10})=\frac{13}{5}$,此时甲、乙速度比为$\frac{18}{5}:\frac{13}{5}=18:13$。
甲到达B地时,需走完剩下的$\frac{2}{5}$路程,这段时间乙走的路程为$\frac{2}{5}×\frac{13}{18}=\frac{13}{45}$。
乙离A地的距离占全程的$\frac{3}{5}-\frac{13}{45}=\frac{27}{45}-\frac{13}{45}=\frac{14}{45}$,已知该距离为14千米,所以A、B两地距离为$14÷\frac{14}{45}=45$千米。
答:A、B两地的距离为45千米。
相遇时,甲、乙路程比等于速度比$3:2$,则相遇时甲行了全程的$\frac{3}{3+2}=\frac{3}{5}$,乙行了全程的$\frac{2}{3+2}=\frac{2}{5}$。
相遇后,甲的速度为$3×(1+\frac{1}{5})=\frac{18}{5}$,乙的速度为$2×(1+\frac{3}{10})=\frac{13}{5}$,此时甲、乙速度比为$\frac{18}{5}:\frac{13}{5}=18:13$。
甲到达B地时,需走完剩下的$\frac{2}{5}$路程,这段时间乙走的路程为$\frac{2}{5}×\frac{13}{18}=\frac{13}{45}$。
乙离A地的距离占全程的$\frac{3}{5}-\frac{13}{45}=\frac{27}{45}-\frac{13}{45}=\frac{14}{45}$,已知该距离为14千米,所以A、B两地距离为$14÷\frac{14}{45}=45$千米。
答:A、B两地的距离为45千米。