5. 小明在使用手机上的计算器计算百分数加法时发现,手机竟然出现了“错误”,当他输入“$10\% + 20\% = $”,手机显示的计算结果是 0.12。经过研究他发现,原来这是因为计算器里的程序是把“$10\% + 20\%$”算成“10%加上它的 20%”。
(1)按照这样的程序,小明输入“$20\% + 30\% = $”,计算器里显示的结果是( )。
(2)小明在这个计算器里输入一个数,又输入“$+50\%$”,得到的结果是 90。他一开始输入的数是( )。
(1)按照这样的程序,小明输入“$20\% + 30\% = $”,计算器里显示的结果是( )。
(2)小明在这个计算器里输入一个数,又输入“$+50\%$”,得到的结果是 90。他一开始输入的数是( )。
答案:
@@5.
(1)0.26
(2)60 提示:
(1)由题意可知,算式表示的含义是20%+30%×20%=0.26。
(2)假设这个数是x,则由题意可列方程为x+50%x=90,解得x=60。
6. 甲、乙两车同时从 A 地开往 B 地,当甲车行至全程的$\frac{5}{7}$处时,乙车超过中点 15 千米,这时甲车比乙车多行 45 千米,A、B 两地相距多少千米?
答案:
@@6.$(45+15)÷(\frac{5}{7}-\frac{1}{2})=280$(千米) 提示:由题意可知,当甲车行至全程的$\frac{5}{7}$处时,甲车超过两地中点(45+15)千米,这段路程占全程的$(\frac{5}{7}-\frac{1}{2})$。
7. 服装厂生产的一款西装每套定价 400 元,领带每条定价 80 元。在促销期间,提供两种优惠方案(只能选择其中的一种方案):
方案 A:买一套西装送一条领带。
方案 B:西装按定价的八折,领带按定价的九折付款。
林阿姨要购买西装 20 套、领带 35 条。请帮她选择一个更省钱的购买方案,通过计算说明。
方案 A:买一套西装送一条领带。
方案 B:西装按定价的八折,领带按定价的九折付款。
林阿姨要购买西装 20 套、领带 35 条。请帮她选择一个更省钱的购买方案,通过计算说明。
答案:
@@7.方案A:20×400+(35-20)×80=9200(元) 方案B:20×(400×80%)+35×(80×90%)=8920(元) 9200>8920 选择方案B更省钱。 提示:分别求出两种方案所需要的价钱,再比较。
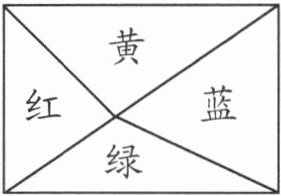
8. 如图,一个长方形分成四个不同的三角形,绿色三角形的面积占长方形面积的 20%,黄色三角形比绿色三角形的面积多 40 平方厘米,绿色三角形的面积是多少平方厘米?

答案:
@@8.50%-20%-20%=10% 40÷10%×20%=80(平方厘米) 提示:黄、绿三角形面积之和是长方形面积的50%,绿色三角形面积占20%,则可知黄色三角形面积占30%,再求出黄色三角形比绿色三角形多占长方形面积的百分比,用多的面积除以多占长方形面积的百分比求出长方形的面积,最后求出绿色三角形的面积。
9. 有大、小两个瓶子,大瓶中盐水的质量是小瓶的 2 倍。大瓶中盐水的含盐率是 20%,小瓶中盐水的含盐率是 35%。将两瓶盐水混合后,盐水的含盐率是多少?
答案:
@@9.假设小瓶中的盐水质量是100克,则大瓶中的盐水质量是200克。200×20%=40(克) 100×35%=35(克) (40+35)÷(200+100)=0.25=25% 提示:此类题可以用设数法来解决,所设的数要尽量方便计算。
10. 甲、乙两种商品的成本共 300 元,甲商品按 30%的利润定价,乙商品按 20%的利润定价,销售时都按定价的 90%销售,结果仍获利 40.2 元,甲商品的成本是多少元? 乐乐先假设两种商品都按 20%的利润来定价,你知道他是怎么算的吗? 试一试!
答案:10@@40.2-[300×(1+20%)×90%-300]=16.2(元) [(1+30%)-(1+20%)]×90%=9%@@16.2÷9%=180(元) 提示:假设两种商品都按20%的利润定价,按定价的90%销售可获利300×(1+20%)×90%-300=24(元),比实际少获利40.2-24=16.2(元),相差的16.2元是因为甲商品是按30%的利润定价的,所以16.2元对应的分率是[(1+30%)-(1+20%)]×90%=9%,那么甲商品的成本是16.2÷9%=180(元)。