1. (1)在括号里填上合适的单位。
一瓶眼药水的含量是 20
一台洗衣机的体积是 630
一个电热水壶的容积是 1.5
一台冰箱说明书上标注的外形尺寸为 $712×667×1888$
(2)用下面的部分材料焊接一个长方体框架(不对铁条进行切割)。如果在这个长方体外面糊上一层包装纸,在里面最多可以放
|铁条长度|25 厘米|20 厘米|15 厘米|9 厘米|
|铁条根数|5|6|3|4|
(3)一张办公桌有 4 个一样的抽屉,每个抽屉长 50 厘米,宽 40 厘米,高 12 厘米,做这些抽屉至少需要
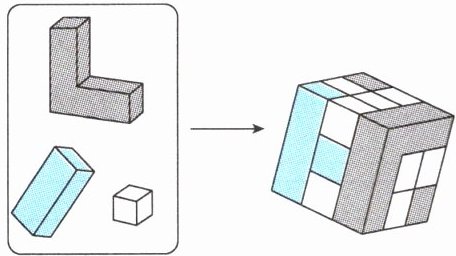
(4)如图,用三种木块摆出一个正方体,这个正方体中一共用了
(5)一个长方体的长、宽、高分别是 $a$ 分米、$b$ 分米、$c(c>5)$ 分米,把高减少 5 分米,表面积减少
(6)一个长方体的棱长总和是 96 厘米,它的长、宽、高的长度比是 $5:4:3$,这个长方体的表面积是
一瓶眼药水的含量是 20
毫升
。一台洗衣机的体积是 630
立方分米
。一个电热水壶的容积是 1.5
升
。一台冰箱说明书上标注的外形尺寸为 $712×667×1888$
毫米
。(2)用下面的部分材料焊接一个长方体框架(不对铁条进行切割)。如果在这个长方体外面糊上一层包装纸,在里面最多可以放
144
个棱长为 3 厘米的小正方体木块。|铁条长度|25 厘米|20 厘米|15 厘米|9 厘米|
|铁条根数|5|6|3|4|
(3)一张办公桌有 4 个一样的抽屉,每个抽屉长 50 厘米,宽 40 厘米,高 12 厘米,做这些抽屉至少需要
166.4
平方分米的木板。(4)如图,用三种木块摆出一个正方体,这个正方体中一共用了
11
个白色木块。
(5)一个长方体的长、宽、高分别是 $a$ 分米、$b$ 分米、$c(c>5)$ 分米,把高减少 5 分米,表面积减少
10a+10b
平方分米,体积减少5ab
立方分米。(6)一个长方体的棱长总和是 96 厘米,它的长、宽、高的长度比是 $5:4:3$,这个长方体的表面积是
376
平方厘米,体积是480
立方厘米。答案:1.
(1)毫升 立方分米 升 毫米
(2)144
(3)166.4
(4)11
(5)10a+10b 5ab
(6)376 480
(1)毫升 立方分米 升 毫米
(2)144
(3)166.4
(4)11
(5)10a+10b 5ab
(6)376 480
2. 一小包纸巾的长、宽、高如图所示(单位:厘米)。如果一小包里有 10 张纸巾,那么每张纸巾的体积是多少立方厘米?如果用一大张塑料纸将 10 小包纸巾以如图方式包起来,需要多少平方厘米的塑料纸?(不考虑耗损)


答案:2.7×3×5÷10=10.5(立方厘米) 长:5×5=25(厘米) 宽:3×2=6(厘米) 高:7厘米 (25×6+6×7+25×7)×2=734(平方厘米)
3. (1)用长 4 分米、宽 2 分米、高 1 分米的长方体木块拼正方体,至少需要(
(2)在一个棱长为 $a$ 的大正方体中,挖去一个棱长为 $b$ 的小正方体。图①中剩下图形的表面积为(

(3)将一个长方体切 4 刀,正好可以切成若干个小正方体(如图),增加的表面积是原来长方体表面积的 $\frac{(

(4)一个大正方体由若干个棱长 1 厘米的小正方体组成,在大正方体的表面涂色,其中只有一个面涂色的小正方体有 24 个,有两个面涂色的小正方体有(
8
)个。(2)在一个棱长为 $a$ 的大正方体中,挖去一个棱长为 $b$ 的小正方体。图①中剩下图形的表面积为(
6a²
),图②中剩下图形的表面积为(6a²+2b²
),图③中剩下图形的表面积为(6a²+4b²
)。
(3)将一个长方体切 4 刀,正好可以切成若干个小正方体(如图),增加的表面积是原来长方体表面积的 $\frac{(
5
)}{(4
)}$。
(4)一个大正方体由若干个棱长 1 厘米的小正方体组成,在大正方体的表面涂色,其中只有一个面涂色的小正方体有 24 个,有两个面涂色的小正方体有(
24
)个。答案:3.
(1)8 提示:长至少要放1个,宽至少要放2个,高至少要放4个,一共需要4×2×1=8(个)。
(2)6a² 6a²+2b² 6a²+4b² 提示:要结合挖去的小正方体的位置来判断表面积是否发生了变化。
(3)$\frac{5}{4}$ 提示:表面积增加了2个上面的面积+4个右面的面积+2个前面的面积,设小正方体棱长为1计算即可。
(4)24 提示:只有一个面涂色的小正方体涂色的面出现在一个面剔除外围一圈小正方形后留下的部分,从题中可知每个面上有24÷6=4(个)涂色的面,因为2×2=4,可知中间正方形的边长是2厘米。大正方体的棱长是4厘米,两个面涂色的小正方体出现在棱上剔除两头顶点上的小正方体的部分,每条棱上有2个,一共有2×12=24(个)。
(1)8 提示:长至少要放1个,宽至少要放2个,高至少要放4个,一共需要4×2×1=8(个)。
(2)6a² 6a²+2b² 6a²+4b² 提示:要结合挖去的小正方体的位置来判断表面积是否发生了变化。
(3)$\frac{5}{4}$ 提示:表面积增加了2个上面的面积+4个右面的面积+2个前面的面积,设小正方体棱长为1计算即可。
(4)24 提示:只有一个面涂色的小正方体涂色的面出现在一个面剔除外围一圈小正方形后留下的部分,从题中可知每个面上有24÷6=4(个)涂色的面,因为2×2=4,可知中间正方形的边长是2厘米。大正方体的棱长是4厘米,两个面涂色的小正方体出现在棱上剔除两头顶点上的小正方体的部分,每条棱上有2个,一共有2×12=24(个)。