1. (2024·威海)一批食品,标准质量为每袋454g,现随机抽取4袋样品进行检测,把超过标准质量的克数用正数表示,不足的克数用负数表示,那么下列记录的最接近标准质量的一袋样品是(
A.+7
B.-5
C.-3
D.+10
C
)A.+7
B.-5
C.-3
D.+10
答案:C
解析:
要判断哪袋样品最接近标准质量,需比较各选项与标准质量差值的绝对值大小,绝对值越小越接近标准质量。
计算各选项的绝对值:
$|+7| = 7$
$|-5| = 5$
$|-3| = 3$
$|+10| = 10$
比较绝对值大小:$3 < 5 < 7 < 10$,故$-3$对应的样品最接近标准质量。
C
计算各选项的绝对值:
$|+7| = 7$
$|-5| = 5$
$|-3| = 3$
$|+10| = 10$
比较绝对值大小:$3 < 5 < 7 < 10$,故$-3$对应的样品最接近标准质量。
C
2. (2024·海门期中)已知有理数x满足|x - 3| = 3 - x,则x的值不可能是(
A.-1
B.0
C.4
D.3
C
)A.-1
B.0
C.4
D.3
答案:C
解析:
解:由绝对值的性质,若|a| = -a,则a ≤ 0。
已知|x - 3| = 3 - x,即|x - 3| = -(x - 3),
所以x - 3 ≤ 0,解得x ≤ 3。
选项中x=4不满足x ≤ 3,
故x的值不可能是4。
答案:C
已知|x - 3| = 3 - x,即|x - 3| = -(x - 3),
所以x - 3 ≤ 0,解得x ≤ 3。
选项中x=4不满足x ≤ 3,
故x的值不可能是4。
答案:C
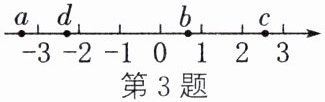
3. [教材P13例4(2)变式]有理数a,b,c,d在数轴上的对应点的位置如图所示,则这四个数中绝对值最大的是(
A.a
B.b
C.c
D.d
A
)
A.a
B.b
C.c
D.d
答案:A
解析:
解:由数轴可知,各数的大致位置为:a在-3附近,d在-2附近,b在0和1之间,c在2和3之间。
根据绝对值的几何意义,一个数的绝对值是它在数轴上对应点到原点的距离。
a到原点的距离约为3,d到原点的距离约为2,b到原点的距离小于1,c到原点的距离约为2.5。
比较各数绝对值大小:|a|>|c|>|d|>|b|。
所以绝对值最大的是a。
答案:A
根据绝对值的几何意义,一个数的绝对值是它在数轴上对应点到原点的距离。
a到原点的距离约为3,d到原点的距离约为2,b到原点的距离小于1,c到原点的距离约为2.5。
比较各数绝对值大小:|a|>|c|>|d|>|b|。
所以绝对值最大的是a。
答案:A
4. 如图,数轴的单位长度为1,如果点B,C表示的数的绝对值相等,那么点A表示的数是(
A.-4
B.-5
C.-6
D.-2
A
)A.-4
B.-5
C.-6
D.-2
答案:A
解析:
解:由图可知,点B与点C之间有4个单位长度。
因为点B,C表示的数的绝对值相等,所以点B和点C表示的数互为相反数,且原点为B,C两点的中点。
因此,点B与点C到原点的距离均为2个单位长度。
则点B表示的数为-2,点C表示的数为2。
又因为点A在点B左侧2个单位长度处,
所以点A表示的数是-2-2=-4。
答案:A
因为点B,C表示的数的绝对值相等,所以点B和点C表示的数互为相反数,且原点为B,C两点的中点。
因此,点B与点C到原点的距离均为2个单位长度。
则点B表示的数为-2,点C表示的数为2。
又因为点A在点B左侧2个单位长度处,
所以点A表示的数是-2-2=-4。
答案:A
5. 有下列说法:① 互为相反数的两个数的绝对值相等;② 绝对值等于本身的数只有正数;③ 不相等的两个数的绝对值一定不相等;④ 绝对值相等的数一定相等.其中,正确的有(
A.1个
B.2个
C.3个
D.4个
A
)A.1个
B.2个
C.3个
D.4个
答案:A
解析:
①互为相反数的两个数的绝对值相等,正确;
②绝对值等于本身的数有正数和0,原说法错误;
③不相等的两个数的绝对值可能相等,如2和-2,原说法错误;
④绝对值相等的数不一定相等,如2和-2,原说法错误。
正确的有1个。
答案:A
②绝对值等于本身的数有正数和0,原说法错误;
③不相等的两个数的绝对值可能相等,如2和-2,原说法错误;
④绝对值相等的数不一定相等,如2和-2,原说法错误。
正确的有1个。
答案:A
6. 已知|a| = $\frac{1}{2}$,|b| = 4,|c| = 5,且有理数a,b,c在数轴上的位置如图所示,则a =

$-\frac{1}{2}$
,b = 4
,c = $-5$
.
答案:$-\frac{1}{2}$ 4 $-5$
解析:
解:由数轴可知,$c < a < 0 < b$。
因为$|a| = \frac{1}{2}$,且$a < 0$,所以$a = -\frac{1}{2}$;
因为$|b| = 4$,且$b > 0$,所以$b = 4$;
因为$|c| = 5$,且$c < 0$,所以$c = -5$。
$-\frac{1}{2}$,$4$,$-5$
因为$|a| = \frac{1}{2}$,且$a < 0$,所以$a = -\frac{1}{2}$;
因为$|b| = 4$,且$b > 0$,所以$b = 4$;
因为$|c| = 5$,且$c < 0$,所以$c = -5$。
$-\frac{1}{2}$,$4$,$-5$
7. (教材P14练习第4题变式)化简:
(1) -|+$\frac{1}{2025}$| =
(2) |+(-20)| =
(3) |-(-$\frac{2}{3}$)| =
(4) |-(+19)| =
(1) -|+$\frac{1}{2025}$| =
$-\frac{1}{2025}$
;(2) |+(-20)| =
20
;(3) |-(-$\frac{2}{3}$)| =
$\frac{2}{3}$
;(4) |-(+19)| =
19
.答案:(1) $-\frac{1}{2025}$;(2) 20;(3) $\frac{2}{3}$;(4) 19
8. (教材P14练习第3题变式)
(1) 若|a| = 6,则a =
(2) 若|-b| = |-9.1|,且b < 0,则b的值为
(3) 若|c - 2025| = 0,则c =
(1) 若|a| = 6,则a =
6 或 -6
;(2) 若|-b| = |-9.1|,且b < 0,则b的值为
-9.1
;(3) 若|c - 2025| = 0,则c =
2025
.答案:(1) 6 或 $-6$;(2) $-9.1$;(3) 2025
解析:
(1) ±6
(2) -9.1
(3) 2025
(2) -9.1
(3) 2025
9. 有下列各数:-2$\frac{1}{2}$,|-4|,-|-4|,0,-(-2$\frac{1}{2}$).请画出数轴,并将这些数在数轴上表示出来.
答案:
如图所示
如图所示
