7. 如图,下列表示角的方法不正确的是 (
A.$∠A$
B.$∠E$
C.$∠α$
D.$∠1$
$\angle MCB$(或$\angle MCN$)
)A.$∠A$
B.$∠E$
C.$∠α$
D.$∠1$
答案：$\angle MCB$(或$\angle MCN$) $\angle AMC$ $\angle CAN$
8. 下列四个图形中,能用$∠1$,$∠AOB$,$∠O$三种方法表示同一个角的是 (
B
)答案：B
9. 如图,分别用三个大写字母表示下列各角：$∠1$为
$\angle MCB$(或$\angle MCN$)
；$∠2$为$\angle AMC$
；$∠3$为$\angle CAN$
.答案：$\angle MCB$(或$\angle MCN$) $\angle AMC$ $\angle CAN$
10. 如图,以 B 为顶点的角有几个？请把它们表示出来. 以 D 为顶点且小于平角的角有几个？请把它们表示出来.
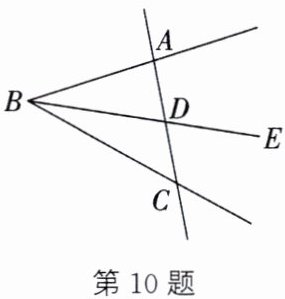
答案：以B为顶点的角有3个，分别是$\angle ABD$(或$\angle ABE$)，$\angle DBC$(或$\angle EBC$),$\angle ABC$ 以D为顶点且小于平角的角有4个,分别是$\angle ADB,\angle ADE,\angle BDC,\angle EDC$
11. 如图,按要求画图,并解答问题：
(1)在$∠AOB$内画 1 条射线$OA_{1}$,此时图中有几个不同的角？
(2)在$∠AOB$内画 2 条不同的射线$OA_{1}$,$OA_{2}$,此时图中有几个不同的角？
(3)在$∠AOB内画(n - 1)条不同的射线OA_{1}$,$OA_{2}$,$OA_{3}$,…,$OA_{n - 1}$,此时图中有几个不同的角？当$n = 99$时呢？
(1)在$∠AOB$内画 1 条射线$OA_{1}$,此时图中有几个不同的角？
(2)在$∠AOB$内画 2 条不同的射线$OA_{1}$,$OA_{2}$,此时图中有几个不同的角？
(3)在$∠AOB内画(n - 1)条不同的射线OA_{1}$,$OA_{2}$,$OA_{3}$,…,$OA_{n - 1}$,此时图中有几个不同的角？当$n = 99$时呢？
答案：(1) 如图①所示 3个 (2) 如图②所示 6个 (3) 如图③所示 $\frac{n(n + 1)}{2}$个 当$n = 99$时,图中有$\frac{99×100}{2}=4950$(个)不同的角
解析：
(1) 图中有3个不同的角。
(2) 图中有6个不同的角。
(3) 图中有$\frac{n(n + 1)}{2}$个不同的角。当$n = 99$时，$\frac{99×100}{2}=4950$，即有4950个不同的角。
(2) 图中有6个不同的角。
(3) 图中有$\frac{n(n + 1)}{2}$个不同的角。当$n = 99$时，$\frac{99×100}{2}=4950$，即有4950个不同的角。