1. (教材 P174 练习第 2 题变式)如图,下列式子错误的是 (
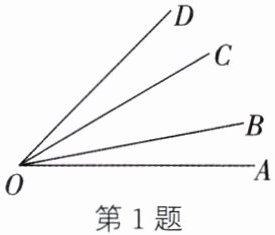
A.$ \angle AOC = \angle AOB + \angle BOC $
B.$ \angle AOC = \angle AOD - \angle COD $
C.$ \angle AOC = \angle AOB + \angle BOD - \angle BOC $
D.$ \angle AOC = \angle AOD - \angle BOD + \angle BOC $
C
)
A.$ \angle AOC = \angle AOB + \angle BOC $
B.$ \angle AOC = \angle AOD - \angle COD $
C.$ \angle AOC = \angle AOB + \angle BOD - \angle BOC $
D.$ \angle AOC = \angle AOD - \angle BOD + \angle BOC $
答案:C
解析:
解:根据图形分析各选项:
A. $\angle AOC = \angle AOB + \angle BOC$,正确;
B. $\angle AOC = \angle AOD - \angle COD$,正确;
C. $\angle AOB + \angle BOD - \angle BOC = \angle AOD - \angle BOC \neq \angle AOC$,错误;
D. $\angle AOD - \angle BOD + \angle BOC = \angle AOB + \angle BOC = \angle AOC$,正确。
答案:C
A. $\angle AOC = \angle AOB + \angle BOC$,正确;
B. $\angle AOC = \angle AOD - \angle COD$,正确;
C. $\angle AOB + \angle BOD - \angle BOC = \angle AOD - \angle BOC \neq \angle AOC$,错误;
D. $\angle AOD - \angle BOD + \angle BOC = \angle AOB + \angle BOC = \angle AOC$,正确。
答案:C
2. (易错题)已知$ \angle AOB = 58 ^ { \circ } 32 ^ { \prime } $,以 $ O $ 为端点作射线 $ OC $,使$ \angle AOC = 42 ^ { \circ } 41 ^ { \prime } $,则$ \angle BOC $的度数为 (
A.$ 15 ^ { \circ } 51 ^ { \prime } $
B.$ 101 ^ { \circ } 13 ^ { \prime } $
C.$ 15 ^ { \circ } 51 ^ { \prime } $或 $ 101 ^ { \circ } 13 ^ { \prime } $
D.$ 16 ^ { \circ } 51 ^ { \prime } $或 $ 101 ^ { \circ } 13 ^ { \prime } $
C
)A.$ 15 ^ { \circ } 51 ^ { \prime } $
B.$ 101 ^ { \circ } 13 ^ { \prime } $
C.$ 15 ^ { \circ } 51 ^ { \prime } $或 $ 101 ^ { \circ } 13 ^ { \prime } $
D.$ 16 ^ { \circ } 51 ^ { \prime } $或 $ 101 ^ { \circ } 13 ^ { \prime } $
答案:C [易错分析]对角的位置情况考虑不全致错.
3. (2025·如皋期末)如图,点 $ O $ 在直线 $ AB $ 上,$ OD $ 平分$ \angle BOC $,$ \angle BOD = 50 ^ { \circ } $,则$ \angle AOC $的度数是
$80^{\circ}$
.答案:$80^{\circ}$
解析:
解:∵OD平分∠BOC,∠BOD=50°,
∴∠BOC=2∠BOD=2×50°=100°.
∵点O在直线AB上,
∴∠AOB=180°,
∴∠AOC=∠AOB - ∠BOC=180° - 100°=80°.
故答案为:80°
∴∠BOC=2∠BOD=2×50°=100°.
∵点O在直线AB上,
∴∠AOB=180°,
∴∠AOC=∠AOB - ∠BOC=180° - 100°=80°.
故答案为:80°
4. 如图,$ BD $ 是$ \angle ABC $的平分线,$ BE $ 是$ \angle CBD $的平分线.若$ \angle CBE = 16 ^ { \circ } $,则$ \angle ABE = $
$48^{\circ}$
.答案:$48^{\circ}$
解析:
解:因为BE是∠CBD的平分线,∠CBE=16°,
所以∠CBD=2∠CBE=2×16°=32°。
因为BD是∠ABC的平分线,
所以∠ABD=∠CBD=32°。
所以∠ABE=∠ABD+∠DBE=32°+16°=48°。
故答案为:48°。
所以∠CBD=2∠CBE=2×16°=32°。
因为BD是∠ABC的平分线,
所以∠ABD=∠CBD=32°。
所以∠ABE=∠ABD+∠DBE=32°+16°=48°。
故答案为:48°。
5. (分类讨论思想)已知$ \angle AOB = 70 ^ { \circ } $,$ \angle BOC = 50 ^ { \circ } $,$ OD $ 是$ \angle AOC $的平分线,则$ \angle BOD $的度数为
$10^{\circ}$或$60^{\circ}$
.答案:$10^{\circ}$或$60^{\circ}$
解析:
解:分两种情况讨论:
情况一:射线OC在∠AOB内部。
∵∠AOB=70°,∠BOC=50°,
∴∠AOC=∠AOB - ∠BOC=70° - 50°=20°。
∵OD是∠AOC的平分线,
∴∠AOD=∠DOC=∠AOC÷2=20°÷2=10°。
∴∠BOD=∠BOC + ∠DOC=50° + 10°=60°。
情况二:射线OC在∠AOB外部。
∵∠AOB=70°,∠BOC=50°,
∴∠AOC=∠AOB + ∠BOC=70° + 50°=120°。
∵OD是∠AOC的平分线,
∴∠AOD=∠DOC=∠AOC÷2=120°÷2=60°。
∴∠BOD=∠DOC - ∠BOC=60° - 50°=10°。
综上,∠BOD的度数为10°或60°。
情况一:射线OC在∠AOB内部。
∵∠AOB=70°,∠BOC=50°,
∴∠AOC=∠AOB - ∠BOC=70° - 50°=20°。
∵OD是∠AOC的平分线,
∴∠AOD=∠DOC=∠AOC÷2=20°÷2=10°。
∴∠BOD=∠BOC + ∠DOC=50° + 10°=60°。
情况二:射线OC在∠AOB外部。
∵∠AOB=70°,∠BOC=50°,
∴∠AOC=∠AOB + ∠BOC=70° + 50°=120°。
∵OD是∠AOC的平分线,
∴∠AOD=∠DOC=∠AOC÷2=120°÷2=60°。
∴∠BOD=∠DOC - ∠BOC=60° - 50°=10°。
综上,∠BOD的度数为10°或60°。
6. (教材 P174 练习第 3 题变式)计算:
(1) $ 33 ^ { \circ } 16 ^ { \prime } 28 ^ { \prime \prime } + 24 ^ { \circ } 46 ^ { \prime } 37 ^ { \prime \prime } $;
(2) $ 95 ^ { \circ } 37 ^ { \prime } 21 ^ { \prime \prime } - 60 ^ { \circ } 52 ^ { \prime } 40 ^ { \prime \prime } $.
(1) $ 33 ^ { \circ } 16 ^ { \prime } 28 ^ { \prime \prime } + 24 ^ { \circ } 46 ^ { \prime } 37 ^ { \prime \prime } $;
(2) $ 95 ^ { \circ } 37 ^ { \prime } 21 ^ { \prime \prime } - 60 ^ { \circ } 52 ^ { \prime } 40 ^ { \prime \prime } $.
答案:(1) $33^{\circ}16'28'' + 24^{\circ}46'37'' = 58^{\circ}3'5''$ (2) $95^{\circ}37'21'' - 60^{\circ}52'40'' = 34^{\circ}44'41''$
解析:
(1) $33^{\circ}16'28'' + 24^{\circ}46'37''$
$=(33^{\circ}+24^{\circ}) + (16'+46') + (28''+37'')$
$=57^{\circ} + 62' + 65''$
$=57^{\circ} + 1^{\circ}2' + 1'5''$
$=58^{\circ}3'5''$
(2) $95^{\circ}37'21'' - 60^{\circ}52'40''$
$=94^{\circ}96'81'' - 60^{\circ}52'40''$
$=(94^{\circ}-60^{\circ}) + (96'-52') + (81''-40'')$
$=34^{\circ}44'41''$
$=(33^{\circ}+24^{\circ}) + (16'+46') + (28''+37'')$
$=57^{\circ} + 62' + 65''$
$=57^{\circ} + 1^{\circ}2' + 1'5''$
$=58^{\circ}3'5''$
(2) $95^{\circ}37'21'' - 60^{\circ}52'40''$
$=94^{\circ}96'81'' - 60^{\circ}52'40''$
$=(94^{\circ}-60^{\circ}) + (96'-52') + (81''-40'')$
$=34^{\circ}44'41''$
7. 如图,点 $ A,O,B $ 在同一条直线上,$ \angle COE = 20 ^ { \circ } 12 ^ { \prime } $,$ OD,OE $ 分别是$ \angle COA $,$ \angle COB $的平分线.
(1) 请你分别计算出$ \angle COB 与 \angle COA $的度数;
(2) 请你计算出$ \angle DOE $的度数.

(1) 请你分别计算出$ \angle COB 与 \angle COA $的度数;
(2) 请你计算出$ \angle DOE $的度数.

答案:(1) 因为 $OE$ 是$\angle COB$ 的平分线,$\angle COE = 20^{\circ}12'$,所以$\angle COB = 2\angle COE = 40^{\circ}24'$。所以$\angle COA = 180^{\circ}-\angle COB = 139^{\circ}36'$ (2) 因为 $OD$,$OE$ 分别是$\angle COA$,$\angle COB$ 的平分线,所以$\angle COD = \frac{1}{2}\angle COA$,$\angle COE = \frac{1}{2}\angle COB$。因为$\angle COA + \angle COB = 180^{\circ}$,所以$\angle COD + \angle COE = \frac{1}{2}\angle COA + \frac{1}{2}\angle COB = \frac{1}{2}(\angle COA + \angle COB) = 90^{\circ}$,即$\angle DOE = 90^{\circ}$
解析:
(1) 因为OE是∠COB的平分线,∠COE=20°12',所以∠COB=2∠COE=2×20°12'=40°24'。因为点A,O,B在同一条直线上,所以∠AOB=180°,所以∠COA=∠AOB - ∠COB=180° - 40°24'=139°36'。
(2) 因为OD,OE分别是∠COA,∠COB的平分线,所以∠COD=1/2∠COA,∠COE=1/2∠COB。所以∠DOE=∠COD + ∠COE=1/2∠COA + 1/2∠COB=1/2(∠COA + ∠COB)。因为∠COA + ∠COB=∠AOB=180°,所以∠DOE=1/2×180°=90°。
(2) 因为OD,OE分别是∠COA,∠COB的平分线,所以∠COD=1/2∠COA,∠COE=1/2∠COB。所以∠DOE=∠COD + ∠COE=1/2∠COA + 1/2∠COB=1/2(∠COA + ∠COB)。因为∠COA + ∠COB=∠AOB=180°,所以∠DOE=1/2×180°=90°。
8. 已知点 $ P $ 在$ \angle MAN $的内部,有下列等式:① $ \angle PAN = \angle MAP $;② $ \angle PAN = \frac { 1 } { 2 } \angle MAN $;③ $ \angle MAP = \frac { 1 } { 2 } \angle MAN $;④ $ \angle MAN = 2 \angle MAP $.其中,能表示射线 $ AP $ 是$ \angle MAN $的平分线的有 (
A.1 个
B.2 个
C.3 个
D.4 个
D
)A.1 个
B.2 个
C.3 个
D.4 个
答案:D
解析:
解:根据角平分线的定义,射线AP是∠MAN的平分线需满足AP在∠MAN内部,且∠MAP=∠PAN=1/2∠MAN,∠MAN=2∠MAP=2∠PAN。
①∠PAN=∠MAP,满足角平分线定义;
②∠PAN=1/2∠MAN,结合点P在内部,可得∠MAP=∠PAN,满足定义;
③∠MAP=1/2∠MAN,同理可得∠MAP=∠PAN,满足定义;
④∠MAN=2∠MAP,可得∠MAP=∠PAN,满足定义。
能表示的有①②③④,共4个。
答案:D
①∠PAN=∠MAP,满足角平分线定义;
②∠PAN=1/2∠MAN,结合点P在内部,可得∠MAP=∠PAN,满足定义;
③∠MAP=1/2∠MAN,同理可得∠MAP=∠PAN,满足定义;
④∠MAN=2∠MAP,可得∠MAP=∠PAN,满足定义。
能表示的有①②③④,共4个。
答案:D