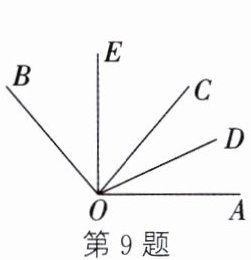
9. 如图,$ OE $ 平分$ \angle BOC $,$ OD $ 平分$ \angle AOC $.若$ \angle AOB = 130 ^ { \circ } $,$ \angle BOE = 40 ^ { \circ } $,则$ \angle AOD $的度数为 (
A.$ 25 ^ { \circ } $
B.$ 30 ^ { \circ } $
C.$ 24 ^ { \circ } $
D.$ 35 ^ { \circ } $
A
)
A.$ 25 ^ { \circ } $
B.$ 30 ^ { \circ } $
C.$ 24 ^ { \circ } $
D.$ 35 ^ { \circ } $
答案:A
解析:
解:∵OE平分∠BOC,∠BOE=40°,
∴∠BOC=2∠BOE=80°,
∵∠AOB=130°,
∴∠AOC=∠AOB - ∠BOC=130° - 80°=50°,
∵OD平分∠AOC,
∴∠AOD=∠AOC/2=50°/2=25°。
答案:A
∴∠BOC=2∠BOE=80°,
∵∠AOB=130°,
∴∠AOC=∠AOB - ∠BOC=130° - 80°=50°,
∵OD平分∠AOC,
∴∠AOD=∠AOC/2=50°/2=25°。
答案:A
10. 如图,$ \angle AOC = \angle BOD = 96 ^ { \circ } $,$ \angle BOC = 56 ^ { \circ } $,则$ \angle AOD $的度数为
$136^{\circ}$
.答案:$136^{\circ}$
解析:
解:由图可知,$\angle AOB = \angle AOC - \angle BOC$。
因为$\angle AOC = 96^{\circ}$,$\angle BOC = 56^{\circ}$,所以$\angle AOB = 96^{\circ} - 56^{\circ} = 40^{\circ}$。
又因为$\angle AOD = \angle AOB + \angle BOD$,且$\angle BOD = 96^{\circ}$,所以$\angle AOD = 40^{\circ} + 96^{\circ} = 136^{\circ}$。
$136^{\circ}$
因为$\angle AOC = 96^{\circ}$,$\angle BOC = 56^{\circ}$,所以$\angle AOB = 96^{\circ} - 56^{\circ} = 40^{\circ}$。
又因为$\angle AOD = \angle AOB + \angle BOD$,且$\angle BOD = 96^{\circ}$,所以$\angle AOD = 40^{\circ} + 96^{\circ} = 136^{\circ}$。
$136^{\circ}$
11. (2024·启东期末)把一副三角尺按如图所示的方式拼在一起,其中 $ B,C,D $ 三点在同一条直线上,$ CM $ 平分$ \angle ACB $,$ CN $ 平分$ \angle DCE $,则$ \angle MCN $的度数为
$127.5^{\circ}$
.答案:$127.5^{\circ}$ 解析:因为 $CM$ 平分$\angle ACB$,$CN$ 平分$\angle DCE$,$\angle ACB = 45^{\circ}$,$\angle DCE = 60^{\circ}$,所以$\angle MCB = \frac{1}{2}\angle ACB = 22.5^{\circ}$,$\angle DCN = \frac{1}{2}\angle DCE = 30^{\circ}$。所以$\angle MCN = 180^{\circ}-\angle MCB - \angle DCN = 180^{\circ}-22.5^{\circ}-30^{\circ}=127.5^{\circ}$。
解析:
解:因为 $CM$ 平分$\angle ACB$,$\angle ACB = 45^{\circ}$,所以$\angle MCB = \frac{1}{2}\angle ACB = 22.5^{\circ}$。
因为 $CN$ 平分$\angle DCE$,$\angle DCE = 60^{\circ}$,所以$\angle DCN = \frac{1}{2}\angle DCE = 30^{\circ}$。
由于 $B,C,D$ 三点在同一条直线上,所以$\angle MCN = 180^{\circ}-\angle MCB - \angle DCN = 180^{\circ}-22.5^{\circ}-30^{\circ}=127.5^{\circ}$。
$127.5^{\circ}$
因为 $CN$ 平分$\angle DCE$,$\angle DCE = 60^{\circ}$,所以$\angle DCN = \frac{1}{2}\angle DCE = 30^{\circ}$。
由于 $B,C,D$ 三点在同一条直线上,所以$\angle MCN = 180^{\circ}-\angle MCB - \angle DCN = 180^{\circ}-22.5^{\circ}-30^{\circ}=127.5^{\circ}$。
$127.5^{\circ}$
12. (教材 P176 练习第 3 题变式)计算:
(1) $ 15 ^ { \circ } 20 ^ { \prime } 35 ^ { \prime \prime } × 6 $;
(2) $ 120 ^ { \circ } 48 ^ { \prime } 35 ^ { \prime \prime } ÷ 5 $.
(1) $ 15 ^ { \circ } 20 ^ { \prime } 35 ^ { \prime \prime } × 6 $;
(2) $ 120 ^ { \circ } 48 ^ { \prime } 35 ^ { \prime \prime } ÷ 5 $.
答案:(1) $15^{\circ}20'35''×6 = 92^{\circ}3'30''$ (2) $120^{\circ}48'35''÷5 = 24^{\circ}9'43''$
解析:
(1) $15^{\circ}20'35''×6$
$=15^{\circ}×6 + 20'×6 + 35''×6$
$=90^{\circ} + 120' + 210''$
$=90^{\circ} + 2^{\circ} + 3' + 30''$(因为$120' = 2^{\circ}$,$210'' = 3'30''$)
$=92^{\circ}3'30''$
(2) $120^{\circ}48'35''÷5$
$=120^{\circ}÷5 + 48'÷5 + 35''÷5$
$=24^{\circ} + 9.6' + 7''$
$=24^{\circ} + 9' + 0.6×60'' + 7''$(因为$0.6' = 0.6×60'' = 36''$)
$=24^{\circ}9'43''$
$=15^{\circ}×6 + 20'×6 + 35''×6$
$=90^{\circ} + 120' + 210''$
$=90^{\circ} + 2^{\circ} + 3' + 30''$(因为$120' = 2^{\circ}$,$210'' = 3'30''$)
$=92^{\circ}3'30''$
(2) $120^{\circ}48'35''÷5$
$=120^{\circ}÷5 + 48'÷5 + 35''÷5$
$=24^{\circ} + 9.6' + 7''$
$=24^{\circ} + 9' + 0.6×60'' + 7''$(因为$0.6' = 0.6×60'' = 36''$)
$=24^{\circ}9'43''$
13. 如图,$ O $ 为直线 $ AB $ 上一点,$ OD $ 平分$ \angle BOC $,$ \angle DOF = 90 ^ { \circ } $.
(1) 若$ \angle BOC = 40 ^ { \circ } $,求$ \angle AOF $的度数;
(2) 若$ \angle COD = 2 \angle EOF $,则 $ OE $ 是图中哪个已知角的平分线?

(1) 若$ \angle BOC = 40 ^ { \circ } $,求$ \angle AOF $的度数;
(2) 若$ \angle COD = 2 \angle EOF $,则 $ OE $ 是图中哪个已知角的平分线?

答案:(1) 因为 $OD$ 平分$\angle BOC$,所以$\angle BOD = \frac{1}{2}\angle BOC = \frac{1}{2}× 40^{\circ}=20^{\circ}$。因为$\angle DOF = 90^{\circ}$,所以$\angle AOF = 180^{\circ}-\angle DOF - \angle BOD = 180^{\circ}-90^{\circ}-20^{\circ}=70^{\circ}$ (2) 设$\angle EOF = \alpha$。因为$\angle COD = 2\angle EOF$,$OD$ 平分$\angle BOC$,所以$\angle COD = \angle BOD = 2\alpha$。因为$\angle DOF = 90^{\circ}$,所以$\angle EOD = \angle DOF - \angle EOF = 90^{\circ}-\alpha$。因为$\angle AOF = 90^{\circ}-\angle BOD = 90^{\circ}-2\alpha$,所以$\angle AOE = \angle AOF + \angle EOF = 90^{\circ}-2\alpha+\alpha = 90^{\circ}-\alpha$。所以$\angle AOE = \angle EOD$。所以 $OE$ 是$\angle AOD$ 的平分线
14. 如图,$ \angle AOB = 90 ^ { \circ } $,$ \angle BOC = 30 ^ { \circ } $,$ OM $ 平分$ \angle AOC $,$ ON $ 平分$ \angle BOC $.
(1) 求$ \angle MON $的度数;
(2) 若将题目中的“$ \angle AOB = 90 ^ { \circ } $”改为“$ \angle AOB = \alpha $”,其他条件不变,求$ \angle MON $的度数;
(3) 若将题目中的“$ \angle BOC = 30 ^ { \circ } $”改为“$ \angle BOC = \beta $($ \beta $ 为锐角)”,其他条件不变,求$ \angle MON $的度数;
(4) 探究:从(1)(2)(3)中,你发现了什么规律?

(1) 求$ \angle MON $的度数;
(2) 若将题目中的“$ \angle AOB = 90 ^ { \circ } $”改为“$ \angle AOB = \alpha $”,其他条件不变,求$ \angle MON $的度数;
(3) 若将题目中的“$ \angle BOC = 30 ^ { \circ } $”改为“$ \angle BOC = \beta $($ \beta $ 为锐角)”,其他条件不变,求$ \angle MON $的度数;
(4) 探究:从(1)(2)(3)中,你发现了什么规律?

答案:(1) 因为$\angle AOB = 90^{\circ}$,$\angle BOC = 30^{\circ}$,所以$\angle AOC = \angle AOB + \angle BOC = 120^{\circ}$。因为 $OM$ 平分$\angle AOC$,$ON$ 平分$\angle BOC$,所以$\angle COM = \frac{1}{2}\angle AOC = 60^{\circ}$,$\angle CON = \frac{1}{2}\angle BOC = 15^{\circ}$。所以$\angle MON = \angle COM - \angle CON = 60^{\circ}-15^{\circ}=45^{\circ}$ (2) 因为$\angle AOB = \alpha$,$\angle BOC = 30^{\circ}$,所以$\angle AOC = \angle AOB + \angle BOC = \alpha + 30^{\circ}$。因为 $OM$ 平分$\angle AOC$,$ON$ 平分$\angle BOC$,所以$\angle COM = \frac{1}{2}\angle AOC = \frac{1}{2}(\alpha + 30^{\circ})$,$\angle CON = \frac{1}{2}\angle BOC = 15^{\circ}$。所以$\angle MON = \angle COM - \angle CON = \frac{1}{2}(\alpha + 30^{\circ})-15^{\circ}=\frac{1}{2}\alpha$ (3) 因为$\angle AOB = 90^{\circ}$,$\angle BOC = \beta$,所以$\angle AOC = \angle AOB + \angle BOC = 90^{\circ}+\beta$。因为 $OM$ 平分$\angle AOC$,$ON$ 平分$\angle BOC$,所以$\angle COM = \frac{1}{2}\angle AOC = \frac{1}{2}(90^{\circ}+\beta)$,$\angle CON = \frac{1}{2}\angle BOC = \frac{1}{2}\beta$。所以$\angle MON = \angle COM - \angle CON = \frac{1}{2}(90^{\circ}+\beta)-\frac{1}{2}\beta = 45^{\circ}$ (4) $\angle MON = \frac{1}{2}\angle AOB$,$\angle MON$ 的度数与$\angle BOC$ 的度数无关