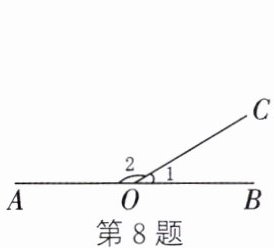
8. 如图,若$\angle AOB = 180^{\circ}$,$\angle 1$ 是锐角,则$\angle 1$ 的余角是 (
A.$\frac{1}{2}\angle 2-\angle 1$
B.$\frac{1}{2}(\angle 2-\angle 1)$
C.$\frac{1}{2}\angle 2-\frac{3}{2}\angle 1$
D.$\frac{1}{3}(\angle 2+\angle 1)$
B
) 
A.$\frac{1}{2}\angle 2-\angle 1$
B.$\frac{1}{2}(\angle 2-\angle 1)$
C.$\frac{1}{2}\angle 2-\frac{3}{2}\angle 1$
D.$\frac{1}{3}(\angle 2+\angle 1)$
答案:B
解析:
解:由图可知∠1+∠2=180°,则∠2=180°-∠1。
∠1的余角为90°-∠1。
将∠2=180°-∠1代入选项:
$\frac{1}{2}(\angle 2 - \angle 1)=\frac{1}{2}[(180^{\circ}-\angle 1)-\angle 1]=\frac{1}{2}(180^{\circ}-2\angle 1)=90^{\circ}-\angle 1$,即∠1的余角。
答案:B
∠1的余角为90°-∠1。
将∠2=180°-∠1代入选项:
$\frac{1}{2}(\angle 2 - \angle 1)=\frac{1}{2}[(180^{\circ}-\angle 1)-\angle 1]=\frac{1}{2}(180^{\circ}-2\angle 1)=90^{\circ}-\angle 1$,即∠1的余角。
答案:B
9. 如图,点 $A$,$O$,$B$ 在同一条直线上,$OC$ 是$\angle AOB$ 的平分线,$OD$,$OE$ 分别是$\angle AOC$ 和$\angle BOC$ 的平分线,那么与$\angle COD$ 互余的角(不包括$\angle COD$ 本身)有 (

A.$1$ 个
B.$2$ 个
C.$3$ 个
D.$0$ 个
C
) 
A.$1$ 个
B.$2$ 个
C.$3$ 个
D.$0$ 个
答案:C
10. 如果一个角的补角的度数是 $128^{\circ}16'26''$,那么它的余角的度数为
38°16'26''
。答案:38°16'26''
解析:
解:设这个角的度数为$x$。
因为互为补角的两个角的和为$180^{\circ}$,所以$x + 128^{\circ}16'26'' = 180^{\circ}$,则$x=180^{\circ}-128^{\circ}16'26'' = 51^{\circ}43'34''$。
又因为互为余角的两个角的和为$90^{\circ}$,所以它的余角的度数为$90^{\circ}-51^{\circ}43'34'' = 38^{\circ}16'26''$。
$38^{\circ}16'26''$
因为互为补角的两个角的和为$180^{\circ}$,所以$x + 128^{\circ}16'26'' = 180^{\circ}$,则$x=180^{\circ}-128^{\circ}16'26'' = 51^{\circ}43'34''$。
又因为互为余角的两个角的和为$90^{\circ}$,所以它的余角的度数为$90^{\circ}-51^{\circ}43'34'' = 38^{\circ}16'26''$。
$38^{\circ}16'26''$
11. (1) 将一副三角尺按如图①所示的方式叠放,使直角顶点重合于点 $O$,则$\angle AOB+\angle DOC= $
(2) 将一副三角尺按如图②所示的方式叠放,则$\angle CDE$ 与$\angle ADC$ 之间的数量关系是

180°
;(2) 将一副三角尺按如图②所示的方式叠放,则$\angle CDE$ 与$\angle ADC$ 之间的数量关系是
∠CDE + ∠ADC = 180°
。
答案:(1)180° (2)∠CDE + ∠ADC = 180°
12. 如图,$\angle AOB$ 和$\angle AOD$ 分别是$\angle AOC$ 的余角和补角,且 $OC$ 是$\angle BOD$ 的平分线。求$\angle AOC$的度数。


答案:由题意,得∠AOB + ∠AOC = 90°,∠AOD + ∠AOC = 180°。可设∠AOC = x°,则∠AOB = (90 - x)°,∠AOD = (180 - x)°。因为OC是∠BOD的平分线,所以∠DOC = ∠BOC。所以∠AOD - ∠AOC = ∠AOC - ∠AOB。所以180 - x - x = x - (90 - x),解得x = 67.5。所以∠AOC = 67.5°
解析:
解:设∠AOC = x°。
∵∠AOB是∠AOC的余角,∴∠AOB = (90 - x)°。
∵∠AOD是∠AOC的补角,∴∠AOD = (180 - x)°。
∵OC是∠BOD的平分线,∴∠DOC = ∠BOC。
∵∠DOC = ∠AOD - ∠AOC,∠BOC = ∠AOC - ∠AOB,
∴180 - x - x = x - (90 - x)。
解得x = 67.5。
∴∠AOC = 67.5°。
∵∠AOB是∠AOC的余角,∴∠AOB = (90 - x)°。
∵∠AOD是∠AOC的补角,∴∠AOD = (180 - x)°。
∵OC是∠BOD的平分线,∴∠DOC = ∠BOC。
∵∠DOC = ∠AOD - ∠AOC,∠BOC = ∠AOC - ∠AOB,
∴180 - x - x = x - (90 - x)。
解得x = 67.5。
∴∠AOC = 67.5°。
13. 如图,$A$,$O$,$B$ 三点在同一条直线上,$\angle BOD$ 与$\angle BOC$ 互补。
(1) $\angle AOC$ 与$\angle BOD$ 相等吗?为什么?
(2) 已知 $OM$ 平分$\angle AOC$,射线 $ON$ 在$\angle COD$ 的内部,且满足$\angle AOC$ 与$\angle MON$ 互余。
① 若$\angle AOC = 32^{\circ}$,求$\angle MON$ 的度数。
② $\angle AON$ 与$\angle DON$ 之间有怎样的数量关系?请说明理由。

(1) $\angle AOC$ 与$\angle BOD$ 相等吗?为什么?
(2) 已知 $OM$ 平分$\angle AOC$,射线 $ON$ 在$\angle COD$ 的内部,且满足$\angle AOC$ 与$\angle MON$ 互余。
① 若$\angle AOC = 32^{\circ}$,求$\angle MON$ 的度数。
② $\angle AON$ 与$\angle DON$ 之间有怎样的数量关系?请说明理由。

答案:
(1)∠AOC = ∠BOD 因为∠BOD与∠BOC互补,所以∠BOD + ∠BOC = 180°。因为∠AOC + ∠BOC = 180°,所以∠AOC = ∠BOD (2)如图,①因为∠AOC与∠MON互余,所以∠MON = 90° - ∠AOC = 58° ②∠AON = ∠DON 理由:因为OM平分∠AOC,所以∠AOC = 2∠AOM,∠COM = ∠AOM。因为∠AOC与∠MON互余,所以∠AOC + ∠MON = 90°。所以易得∠AON = 90° - ∠AOM。所以∠CON = 90° - 3∠AOM。因为∠BOD与∠BOC互补,所以∠BOD + ∠BOC = 180°。所以∠CON + ∠DON + 2∠BOD = 180°。又因为∠BOD = ∠AOC = 2∠AOM,所以∠DON = 180° - ∠CON - 2∠BOD = 180° - (90° - 3∠AOM) - 4∠AOM = 90° - ∠AOM。所以∠AON = ∠DON。
(1)∠AOC = ∠BOD 因为∠BOD与∠BOC互补,所以∠BOD + ∠BOC = 180°。因为∠AOC + ∠BOC = 180°,所以∠AOC = ∠BOD (2)如图,①因为∠AOC与∠MON互余,所以∠MON = 90° - ∠AOC = 58° ②∠AON = ∠DON 理由:因为OM平分∠AOC,所以∠AOC = 2∠AOM,∠COM = ∠AOM。因为∠AOC与∠MON互余,所以∠AOC + ∠MON = 90°。所以易得∠AON = 90° - ∠AOM。所以∠CON = 90° - 3∠AOM。因为∠BOD与∠BOC互补,所以∠BOD + ∠BOC = 180°。所以∠CON + ∠DON + 2∠BOD = 180°。又因为∠BOD = ∠AOC = 2∠AOM,所以∠DON = 180° - ∠CON - 2∠BOD = 180° - (90° - 3∠AOM) - 4∠AOM = 90° - ∠AOM。所以∠AON = ∠DON。
