1. 如果一个角的余角比它的补角的$\frac {1}{3}$还少$20^{\circ }$,那么这个角的度数是
$75^{\circ}$
.答案:$75^{\circ}$
解析:
解:设这个角的度数是$x^{\circ}$,则它的余角是$(90 - x)^{\circ}$,补角是$(180 - x)^{\circ}$。
根据题意可得:$90 - x = \frac{1}{3}(180 - x) - 20$
去分母:$3(90 - x) = 180 - x - 60$
去括号:$270 - 3x = 120 - x$
移项:$-3x + x = 120 - 270$
合并同类项:$-2x = -150$
系数化为1:$x = 75$
答:这个角的度数是$75^{\circ}$。
根据题意可得:$90 - x = \frac{1}{3}(180 - x) - 20$
去分母:$3(90 - x) = 180 - x - 60$
去括号:$270 - 3x = 120 - x$
移项:$-3x + x = 120 - 270$
合并同类项:$-2x = -150$
系数化为1:$x = 75$
答:这个角的度数是$75^{\circ}$。
2. 如图,C,D 是线段 AB 上的两点,$CD= 1cm$,M 是 AD 的中点,N 是 BC 的中点,且$MN= 3.5cm$,则$AB= $
8
cm.答案:$8$
3. 如图,O 是直线 AD 上一点,且$∠BOC= \frac {1}{3}∠AOC= \frac {2}{3}∠COD$.求$∠BOC$的度数.
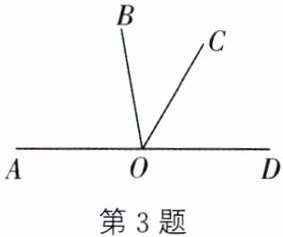

答案:设$\angle BOC$的度数为$x$。因为$\angle BOC=\frac{1}{3}\angle AOC=\frac{2}{3}\angle COD$,所以$\angle AOC = 3x$,$\angle COD=\frac{3}{2}x$。因为$\angle AOC+\angle COD = 180^{\circ}$,所以$3x+\frac{3}{2}x = 180^{\circ}$,解得$x = 40^{\circ}$。所以$\angle BOC$的度数为$40^{\circ}$
解析:
解:设∠BOC的度数为x。
因为∠BOC = $\frac{1}{3}$∠AOC = $\frac{2}{3}$∠COD,
所以∠AOC = 3x,∠COD = $\frac{3}{2}$x。
由于O是直线AD上一点,
所以∠AOC + ∠COD = 180°,
即3x + $\frac{3}{2}$x = 180°,
解得x = 40°。
因此,∠BOC的度数为40°。
因为∠BOC = $\frac{1}{3}$∠AOC = $\frac{2}{3}$∠COD,
所以∠AOC = 3x,∠COD = $\frac{3}{2}$x。
由于O是直线AD上一点,
所以∠AOC + ∠COD = 180°,
即3x + $\frac{3}{2}$x = 180°,
解得x = 40°。
因此,∠BOC的度数为40°。
4. 如图,B,C 两点把线段 AD 分成$2:5:3的三部分(BC>CD>AB)$,M 为 AD 的中点,$BM= 6cm$,求 CM 和 AD 的长.


答案:由题意,可设$AB = 2x cm$,$BC = 5x cm$,$CD = 3x cm$,所以$AD = AB + BC + CD = 10x cm$。因为$M$是$AD$的中点,所以$AM = MD=\frac{1}{2}AD = 5x cm$。所以$BM = AM - AB = 5x - 2x = 3x(cm)$。因为$BM = 6cm$,所以$3x = 6$,解得$x = 2$。所以$BC = 10cm$,$AD = 20cm$。所以$CM = BC - BM = 4cm$
解析:
解:设$AB = 2x\ \text{cm}$,$BC = 5x\ \text{cm}$,$CD = 3x\ \text{cm}$,则$AD = AB + BC + CD = 2x + 5x + 3x = 10x\ \text{cm}$。
因为$M$是$AD$的中点,所以$AM=\frac{1}{2}AD = 5x\ \text{cm}$。
所以$BM = AM - AB = 5x - 2x = 3x\ \text{cm}$。
因为$BM = 6\ \text{cm}$,所以$3x = 6$,解得$x = 2$。
因此,$AD = 10x = 10×2 = 20\ \text{cm}$,$BC = 5x = 10\ \text{cm}$。
所以$CM = BC - BM = 10 - 6 = 4\ \text{cm}$。
答:$CM$的长为$4\ \text{cm}$,$AD$的长为$20\ \text{cm}$。
因为$M$是$AD$的中点,所以$AM=\frac{1}{2}AD = 5x\ \text{cm}$。
所以$BM = AM - AB = 5x - 2x = 3x\ \text{cm}$。
因为$BM = 6\ \text{cm}$,所以$3x = 6$,解得$x = 2$。
因此,$AD = 10x = 10×2 = 20\ \text{cm}$,$BC = 5x = 10\ \text{cm}$。
所以$CM = BC - BM = 10 - 6 = 4\ \text{cm}$。
答:$CM$的长为$4\ \text{cm}$,$AD$的长为$20\ \text{cm}$。
5. 如图,$∠AOB= n^{\circ }$,平面内有一射线 OM,且$∠AOM= 2∠BOM$.若 ON 平分$∠BOM$,则$∠AON= $

$\frac{5}{6}n^{\circ}$或$\frac{3}{2}n^{\circ}$
(用含n的代数式表示).
答案:$\frac{5}{6}n^{\circ}$或$\frac{3}{2}n^{\circ}$
解析:
情况一:射线OM在∠AOB内部
∵∠AOM=2∠BOM,∠AOB=∠AOM+∠BOM=n°,
∴2∠BOM+∠BOM=n°,解得∠BOM=$\frac{n}{3}°$,∠AOM=$\frac{2n}{3}°$.
∵ON平分∠BOM,∴∠BON=$\frac{1}{2}$∠BOM=$\frac{n}{6}°$.
∴∠AON=∠AOB-∠BON=$n°-\frac{n}{6}°=\frac{5n}{6}°$.
情况二:射线OM在∠AOB外部
∵∠AOM=2∠BOM,∠AOM=∠AOB+∠BOM=n°+∠BOM,
∴2∠BOM=n°+∠BOM,解得∠BOM=n°,∠AOM=2n°.
∵ON平分∠BOM,∴∠BON=$\frac{1}{2}$∠BOM=$\frac{n}{2}°$.
∴∠AON=∠AOB+∠BON=$n°+\frac{n}{2}°=\frac{3n}{2}°$.
综上,∠AON=$\frac{5}{6}n°$或$\frac{3}{2}n°$.
$\boxed{\frac{5}{6}n^{\circ} \text{或} \frac{3}{2}n^{\circ}}$
∵∠AOM=2∠BOM,∠AOB=∠AOM+∠BOM=n°,
∴2∠BOM+∠BOM=n°,解得∠BOM=$\frac{n}{3}°$,∠AOM=$\frac{2n}{3}°$.
∵ON平分∠BOM,∴∠BON=$\frac{1}{2}$∠BOM=$\frac{n}{6}°$.
∴∠AON=∠AOB-∠BON=$n°-\frac{n}{6}°=\frac{5n}{6}°$.
情况二:射线OM在∠AOB外部
∵∠AOM=2∠BOM,∠AOM=∠AOB+∠BOM=n°+∠BOM,
∴2∠BOM=n°+∠BOM,解得∠BOM=n°,∠AOM=2n°.
∵ON平分∠BOM,∴∠BON=$\frac{1}{2}$∠BOM=$\frac{n}{2}°$.
∴∠AON=∠AOB+∠BON=$n°+\frac{n}{2}°=\frac{3n}{2}°$.
综上,∠AON=$\frac{5}{6}n°$或$\frac{3}{2}n°$.
$\boxed{\frac{5}{6}n^{\circ} \text{或} \frac{3}{2}n^{\circ}}$
6. 如图,M 为线段 AC 的中点,点 B 在线段 AC 上,N 为直线 AC 上的一点.若$\frac {CN}{BN}= \frac {1}{2},AC= 10,BC= 4$,则线段 MN 的长为
$\frac{11}{3}$或$9$
.答案:$\frac{11}{3}$或$9$
解析:
解:
情况1:点N在线段BC上
设 $CN = x$,则 $BN = 2x$。
$\because BC = 4$,$\therefore BN + CN = BC$,即 $2x + x = 4$,解得 $x = \frac{4}{3}$。
$\because M$为AC中点,$AC = 10$,$\therefore MC = \frac{1}{2}AC = 5$。
$\because BC = 4$,$\therefore MB = MC - BC = 5 - 4 = 1$。
$\therefore MN = MB + BN = 1 + 2x = 1 + \frac{8}{3} = \frac{11}{3}$。
情况2:点N在BC延长线上
设 $CN = x$,则 $BN = 2x$。
$\because BN = BC + CN$,即 $2x = 4 + x$,解得 $x = 4$。
$\therefore MN = MC + CN = 5 + 4 = 9$。
综上,线段MN的长为 $\frac{11}{3}$或$9$。
答案:$\frac{11}{3}$或$9$
情况1:点N在线段BC上
设 $CN = x$,则 $BN = 2x$。
$\because BC = 4$,$\therefore BN + CN = BC$,即 $2x + x = 4$,解得 $x = \frac{4}{3}$。
$\because M$为AC中点,$AC = 10$,$\therefore MC = \frac{1}{2}AC = 5$。
$\because BC = 4$,$\therefore MB = MC - BC = 5 - 4 = 1$。
$\therefore MN = MB + BN = 1 + 2x = 1 + \frac{8}{3} = \frac{11}{3}$。
情况2:点N在BC延长线上
设 $CN = x$,则 $BN = 2x$。
$\because BN = BC + CN$,即 $2x = 4 + x$,解得 $x = 4$。
$\therefore MN = MC + CN = 5 + 4 = 9$。
综上,线段MN的长为 $\frac{11}{3}$或$9$。
答案:$\frac{11}{3}$或$9$
7. 已知线段$AB= 12$,在线段 AB 上有 C,D,M,N 四点,且$AC:CD:DB= 1:2:3,AM= \frac {1}{2}AC,DN= \frac {1}{4}DB$.求线段 MN 的长.
答案:因为$AB = 12$,$AC:CD:DB = 1:2:3$,所以$AC=\frac{1}{6}×12 = 2$,$CD=\frac{2}{6}×12 = 4$,$DB=\frac{3}{6}×12 = 6$。所以$AM=\frac{1}{2}AC = 1$,$DN=\frac{1}{4}DB=\frac{3}{2}$。①如图①,当点$N$在点$D$右侧时,$MN = MC + CD + DN = 2 - 1 + 4+\frac{3}{2}=\frac{13}{2}$;②如图②,当点$N$在点$D$左侧时,$MN = MC + CD - DN = 2 - 1 + 4-\frac{3}{2}=\frac{7}{2}$。综上所述,线段$MN$的长为$\frac{13}{2}$或$\frac{7}{2}$