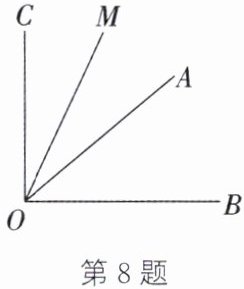
8. 已知$∠AOB= α(30^{\circ }<α<45^{\circ }),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD$,OM 平分$∠AOC$,ON 平分$∠BOD$.
(1) 如图,当$α=40^{\circ }$,且射线 OM 在$∠AOB$的外部时,用直尺、量角器画出射线 OD,ON 的准确位置;
(2) 求(1)中$∠MON$的度数,要求写出计算过程;
(3) 当射线 OM 在$∠AOB$的内部时,用含α的式子表示$∠MON$的度数(直接写出结果).
(1) 如图,当$α=40^{\circ }$,且射线 OM 在$∠AOB$的外部时,用直尺、量角器画出射线 OD,ON 的准确位置;
(2) 求(1)中$∠MON$的度数,要求写出计算过程;
(3) 当射线 OM 在$∠AOB$的内部时,用含α的式子表示$∠MON$的度数(直接写出结果).

答案:(1)如图①②所示 (2)因为$\angle AOB = 40^{\circ}$,$\angle AOB$的余角为$\angle AOC$,$\angle AOB$的补角为$\angle BOD$,所以$\angle AOC = 90^{\circ}-\angle AOB = 50^{\circ}$,$\angle BOD = 180^{\circ}-\angle AOB = 140^{\circ}$。因为$OM$平分$\angle AOC$,$ON$平分$\angle BOD$,所以$\angle MOA=\frac{1}{2}\angle AOC=\frac{1}{2}×50^{\circ}=25^{\circ}$,$\angle BON=\frac{1}{2}\angle BOD=\frac{1}{2}×140^{\circ}=70^{\circ}$。①如图①,$\angle MON=\angle MOA+\angle AOB+\angle BON = 25^{\circ}+40^{\circ}+70^{\circ}=135^{\circ}$。②如图②,$\angle MON=\angle BON-\angle MOA-\angle AOB = 70^{\circ}-25^{\circ}-40^{\circ}=5^{\circ}$。所以$\angle MON$的度数为$135^{\circ}$或$5^{\circ}$ (3)如图③④,$\angle MON=\alpha + 45^{\circ}$或$135^{\circ}-2\alpha$
解析:
(1)如图①②所示。
(2)解:因为∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,
所以∠AOC=90°-∠AOB=50°,∠BOD=180°-∠AOB=140°。
因为OM平分∠AOC,ON平分∠BOD,
所以∠MOA=1/2∠AOC=25°,∠BON=1/2∠BOD=70°。
①如图①,∠MON=∠MOA+∠AOB+∠BON=25°+40°+70°=135°。
②如图②,∠MON=∠BON-∠MOA-∠AOB=70°-25°-40°=5°。
所以∠MON的度数为135°或5°。
(3)∠MON=α+45°或135°-2α。
(2)解:因为∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,
所以∠AOC=90°-∠AOB=50°,∠BOD=180°-∠AOB=140°。
因为OM平分∠AOC,ON平分∠BOD,
所以∠MOA=1/2∠AOC=25°,∠BON=1/2∠BOD=70°。
①如图①,∠MON=∠MOA+∠AOB+∠BON=25°+40°+70°=135°。
②如图②,∠MON=∠BON-∠MOA-∠AOB=70°-25°-40°=5°。
所以∠MON的度数为135°或5°。
(3)∠MON=α+45°或135°-2α。
9. 如图,C,D 是线段 AB 上的任意两点,E 是 AC 的中点,F 是 BD 的中点.如果$EF= m,CD= n$,那么线段 AB 的长度为 (

A.$m+n$
B.$2m+n$
C.$2m-n$
D.$3m-2n$
C
)
A.$m+n$
B.$2m+n$
C.$2m-n$
D.$3m-2n$
答案:$C$
解析:
解:因为E是AC的中点,所以AE=EC。
因为F是BD的中点,所以DF=FB。
由图可知,EF=EC+CD+DF=m,CD=n,
所以EC+DF=m-n。
因为AE=EC,DF=FB,
所以AE+FB=EC+DF=m-n。
AB=AE+EF+FB=(AE+FB)+EF=(m-n)+m=2m-n。
答案:C
因为F是BD的中点,所以DF=FB。
由图可知,EF=EC+CD+DF=m,CD=n,
所以EC+DF=m-n。
因为AE=EC,DF=FB,
所以AE+FB=EC+DF=m-n。
AB=AE+EF+FB=(AE+FB)+EF=(m-n)+m=2m-n。
答案:C
10. 如图,在长方形纸片 ABCD 中,M 为边 AD 的中点.将纸片沿 BM,CM 折叠,使点 A 落在点$A_{1}$处,点 D 落在点$D_{1}$处.若$∠1= 30^{\circ }$,则$∠BMC$的度数为____
$105^{\circ}$
.答案:$105^{\circ}$
解析:
解:
∵四边形ABCD是长方形,
∴∠A=∠D=90°,AD//BC。
由折叠性质得:∠A=∠MA₁B=90°,∠D=∠MD₁C=90°,∠AMB=∠A₁MB,∠DMC=∠D₁MC。
∵∠1=30°,
∴∠A₁MD₁=30°,
∴∠A₁MB + ∠D₁MC = (180° - 30°)÷2 = 75°(平角定义及折叠后角的等量关系)。
∵AD//BC,
∴∠AMB=∠MBC,∠DMC=∠MCB(两直线平行,内错角相等)。
在△BMC中,∠BMC=180° - (∠MBC + ∠MCB)=180° - 75°=105°。
105°
∵四边形ABCD是长方形,
∴∠A=∠D=90°,AD//BC。
由折叠性质得:∠A=∠MA₁B=90°,∠D=∠MD₁C=90°,∠AMB=∠A₁MB,∠DMC=∠D₁MC。
∵∠1=30°,
∴∠A₁MD₁=30°,
∴∠A₁MB + ∠D₁MC = (180° - 30°)÷2 = 75°(平角定义及折叠后角的等量关系)。
∵AD//BC,
∴∠AMB=∠MBC,∠DMC=∠MCB(两直线平行,内错角相等)。
在△BMC中,∠BMC=180° - (∠MBC + ∠MCB)=180° - 75°=105°。
105°
11. 如图,C,D 是线段 AB 上的两点,已知$AB= 10cm,CD= 3cm$,则以 A,C,D,B 为端点的所有线段长度之和为
33
cm.答案:$33$
解析:
以A,C,D,B为端点的线段有AC,AD,AB,CD,CB,DB。
长度之和为AC+AD+AB+CD+CB+DB。
因为AD=AC+CD,CB=CD+DB,
所以原式=AC+(AC+CD)+AB+CD+(CD+DB)+DB
=AC+AC+CD+AB+CD+CD+DB+DB
=2AC+2DB+3CD+AB。
又因为AC+DB=AB-CD=10-3=7cm,
所以原式=2×7+3×3+10=14+9+10=33cm。
33
长度之和为AC+AD+AB+CD+CB+DB。
因为AD=AC+CD,CB=CD+DB,
所以原式=AC+(AC+CD)+AB+CD+(CD+DB)+DB
=AC+AC+CD+AB+CD+CD+DB+DB
=2AC+2DB+3CD+AB。
又因为AC+DB=AB-CD=10-3=7cm,
所以原式=2×7+3×3+10=14+9+10=33cm。
33
12. 如图,$∠AOB$是平角,OM,ON 分别是$∠AOC,∠BOD$的平分线.
(1) 当$∠MON= 140^{\circ }$时,求$∠COD$的度数;
(2) 当$∠COD= α$时,求$∠MON$的度数.

(1) 当$∠MON= 140^{\circ }$时,求$∠COD$的度数;
(2) 当$∠COD= α$时,求$∠MON$的度数.

答案:(1)因为$\angle AOB$是平角,所以$\angle AOB = 180^{\circ}$。因为$OM$,$ON$分别是$\angle AOC$,$\angle BOD$的平分线,所以$\angle AOC = 2\angle AOM$,$\angle BOD = 2\angle BON$。所以$\angle COD = 180^{\circ}-(\angle AOC+\angle BOD)=180^{\circ}-2(\angle AOM+\angle BON)=180^{\circ}-2(180^{\circ}-\angle MON)=2\angle MON - 180^{\circ}=2×140^{\circ}-180^{\circ}=100^{\circ}$ (2)$\angle MON=\angle MOC+\angle COD+\angle DON=\frac{1}{2}\angle AOC+\frac{1}{2}\angle BOD+\angle COD=\frac{1}{2}(180^{\circ}-\angle COD)+\angle COD=90^{\circ}+\frac{1}{2}\angle COD=90^{\circ}+\frac{1}{2}\alpha$
解析:
(1)
∵∠AOB是平角,
∴∠AOB=180°。
∵OM,ON分别是∠AOC,∠BOD的平分线,
∴∠AOC=2∠AOM,∠BOD=2∠BON。
∵∠AOM+∠MON+∠BON=∠AOB,
∴∠AOM+∠BON=∠AOB-∠MON=180°-140°=40°。
∴∠AOC+∠BOD=2(∠AOM+∠BON)=80°。
∴∠COD=∠AOB-(∠AOC+∠BOD)=180°-80°=100°。
(2)
∵∠AOB是平角,
∴∠AOC+∠COD+∠BOD=180°。
∵∠COD=α,
∴∠AOC+∠BOD=180°-α。
∵OM,ON分别是∠AOC,∠BOD的平分线,
∴∠MOC=1/2∠AOC,∠DON=1/2∠BOD。
∴∠MOC+∠DON=1/2(∠AOC+∠BOD)=1/2(180°-α)=90°-1/2α。
∴∠MON=∠MOC+∠COD+∠DON=90°-1/2α+α=90°+1/2α。
∵∠AOB是平角,
∴∠AOB=180°。
∵OM,ON分别是∠AOC,∠BOD的平分线,
∴∠AOC=2∠AOM,∠BOD=2∠BON。
∵∠AOM+∠MON+∠BON=∠AOB,
∴∠AOM+∠BON=∠AOB-∠MON=180°-140°=40°。
∴∠AOC+∠BOD=2(∠AOM+∠BON)=80°。
∴∠COD=∠AOB-(∠AOC+∠BOD)=180°-80°=100°。
(2)
∵∠AOB是平角,
∴∠AOC+∠COD+∠BOD=180°。
∵∠COD=α,
∴∠AOC+∠BOD=180°-α。
∵OM,ON分别是∠AOC,∠BOD的平分线,
∴∠MOC=1/2∠AOC,∠DON=1/2∠BOD。
∴∠MOC+∠DON=1/2(∠AOC+∠BOD)=1/2(180°-α)=90°-1/2α。
∴∠MON=∠MOC+∠COD+∠DON=90°-1/2α+α=90°+1/2α。