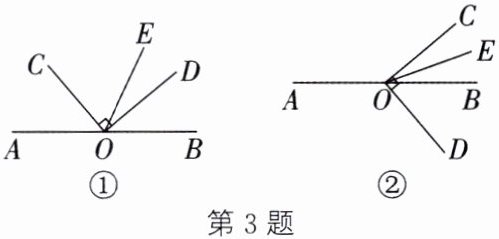
3. O 是直线 AB 上一点,$ ∠COD $ 是直角,OE 平分 $ ∠BOC $.
(1) 如图①,若 $ ∠DOE = 25^{\circ} $,求 $ ∠AOC $ 的度数;
(2) 如图②,若 $ ∠DOE = \alpha $,求 $ ∠AOC $ 的度数(用含 α 的式子表示),并探究 $ ∠DOE $ 与 $ ∠AOC $ 之间的数量关系.
(1) 如图①,若 $ ∠DOE = 25^{\circ} $,求 $ ∠AOC $ 的度数;
(2) 如图②,若 $ ∠DOE = \alpha $,求 $ ∠AOC $ 的度数(用含 α 的式子表示),并探究 $ ∠DOE $ 与 $ ∠AOC $ 之间的数量关系.

答案:3. (1) 因为 $ \angle COD = 90^{\circ} $,$ \angle DOE = 25^{\circ} $,所以 $ \angle COE = \angle COD - \angle DOE = 90^{\circ} - 25^{\circ} = 65^{\circ} $。又因为 $ OE $ 平分 $ \angle BOC $,所以 $ \angle BOC = 2\angle COE = 130^{\circ} $。所以 $ \angle AOC = 180^{\circ} - \angle BOC = 180^{\circ} - 130^{\circ} = 50^{\circ} $ (2) 因为 $ \angle COD = 90^{\circ} $,$ \angle DOE = \alpha $,所以 $ \angle COE = \angle COD - \angle DOE = 90^{\circ} - \alpha $。又因为 $ OE $ 平分 $ \angle BOC $,所以 $ \angle BOC = 2\angle COE = 180^{\circ} - 2\alpha $。所以 $ \angle AOC = 180^{\circ} - \angle BOC = 180^{\circ} - (180^{\circ} - 2\alpha) = 2\alpha $。所以 $ \angle DOE = \frac{1}{2}\angle AOC $
4. (1) 一个角的平分线
(2) 若 $ ∠AOB = 60^{\circ} $,射线 OC 为 $ ∠AOB $ 的“优线”,则 $ ∠AOC $ 的度数为
(3) 如图②,$ ∠AOB = 120^{\circ} $,射线 OP 从 OA 处出发,绕点 O 以每秒 $ 2^{\circ} $ 的速度按顺时针方向旋转,射线 OQ 从 OB 处出发,绕点 O 以每秒 $ 1^{\circ} $ 的速度按逆时针方向旋转,两条射线同时旋转,至 OP,OQ 相遇时停止,设旋转的时间为 t s,问:t 为何值时,射线 OP 是 $ ∠AOQ $ 的“优线”?

是
这个角的“优线”(填“是”或“不是”);一个角共有3
条“优线”.(2) 若 $ ∠AOB = 60^{\circ} $,射线 OC 为 $ ∠AOB $ 的“优线”,则 $ ∠AOC $ 的度数为
$ 30^{\circ} $ 或 $ 20^{\circ} $ 或 $ 40^{\circ} $
.(3) 如图②,$ ∠AOB = 120^{\circ} $,射线 OP 从 OA 处出发,绕点 O 以每秒 $ 2^{\circ} $ 的速度按顺时针方向旋转,射线 OQ 从 OB 处出发,绕点 O 以每秒 $ 1^{\circ} $ 的速度按逆时针方向旋转,两条射线同时旋转,至 OP,OQ 相遇时停止,设旋转的时间为 t s,问:t 为何值时,射线 OP 是 $ ∠AOQ $ 的“优线”?

根据题意,得 $ \angle AOP = (2t)^{\circ} $,$ \angle BOQ = t^{\circ} $,则 $ \angle AOQ = \angle AOB - \angle BOQ = (120 - t)^{\circ} $,$ \angle POQ = \angle AOQ - \angle AOP = (120 - 3t)^{\circ} $。① 当 $ \angle AOP = \frac{1}{2}\angle AOQ $ 时,即 $ 2t = \frac{1}{2}(120 - t) $,解得 $ t = 24 $(经检验,符合题意)。② 当 $ \angle AOP = \frac{1}{2}\angle POQ $ 时,即 $ 2t = \frac{1}{2}(120 - 3t) $,解得 $ t = \frac{120}{7} $(经检验,符合题意)。③ 当 $ \angle POQ = \frac{1}{2}\angle AOP $ 时,即 $ 120 - 3t = t $,解得 $ t = 30 $(经检验,符合题意)。综上所述,当 $ t $ 的值为 24 或 $ \frac{120}{7} $ 或 30 时,射线 $ OP $ 是 $ \angle AOQ $ 的“优线”
答案:4. (1) 是 3 (2) $ 30^{\circ} $ 或 $ 20^{\circ} $ 或 $ 40^{\circ} $ (3) 根据题意,得 $ \angle AOP = (2t)^{\circ} $,$ \angle BOQ = t^{\circ} $,则 $ \angle AOQ = \angle AOB - \angle BOQ = (120 - t)^{\circ} $,$ \angle POQ = \angle AOQ - \angle AOP = (120 - 3t)^{\circ} $。① 当 $ \angle AOP = \frac{1}{2}\angle AOQ $ 时,即 $ 2t = \frac{1}{2}(120 - t) $,解得 $ t = 24 $(经检验,符合题意)。② 当 $ \angle AOP = \frac{1}{2}\angle POQ $ 时,即 $ 2t = \frac{1}{2}(120 - 3t) $,解得 $ t = \frac{120}{7} $(经检验,符合题意)。③ 当 $ \angle POQ = \frac{1}{2}\angle AOP $ 时,即 $ 120 - 3t = t $,解得 $ t = 30 $(经检验,符合题意)。综上所述,当 $ t $ 的值为 24 或 $ \frac{120}{7} $ 或 30 时,射线 $ OP $ 是 $ \angle AOQ $ 的“优线”