8. 计算:
(1) 30°52'+43°50'=
(2) 106°9'-34°58'=
(1) 30°52'+43°50'=
74°42'
;(2) 106°9'-34°58'=
71°11'
.答案:(1)$74^{\circ}42'$ (2)$71^{\circ}11'$
解析:
(1) $30^{\circ}52' + 43^{\circ}50'$
$=(30^{\circ} + 43^{\circ}) + (52' + 50')$
$=73^{\circ} + 102'$
$=73^{\circ} + 1^{\circ}42'$
$=74^{\circ}42'$
(2) $106^{\circ}9' - 34^{\circ}58'$
$=105^{\circ}69' - 34^{\circ}58'$
$=(105^{\circ} - 34^{\circ}) + (69' - 58')$
$=71^{\circ} + 11'$
$=71^{\circ}11'$
(1) $74^{\circ}42'$;(2) $71^{\circ}11'$
$=(30^{\circ} + 43^{\circ}) + (52' + 50')$
$=73^{\circ} + 102'$
$=73^{\circ} + 1^{\circ}42'$
$=74^{\circ}42'$
(2) $106^{\circ}9' - 34^{\circ}58'$
$=105^{\circ}69' - 34^{\circ}58'$
$=(105^{\circ} - 34^{\circ}) + (69' - 58')$
$=71^{\circ} + 11'$
$=71^{\circ}11'$
(1) $74^{\circ}42'$;(2) $71^{\circ}11'$
9. 9时40分时,时钟的时针与分针所夹角的度数为
50°
.答案:$50^{\circ}$
解析:
解:时针每小时走$30^{\circ}$,每分钟走$0.5^{\circ}$;分针每分钟走$6^{\circ}$。
9时整,时针与分针夹角为$9×30^{\circ}=270^{\circ}$。
40分钟内,时针走了$40×0.5^{\circ}=20^{\circ}$,分针走了$40×6^{\circ}=240^{\circ}$。
9时40分,时针位置为$270^{\circ}+20^{\circ}=290^{\circ}$,分针位置为$240^{\circ}$。
夹角为$|290^{\circ}-240^{\circ}|=50^{\circ}$。
$50^{\circ}$
9时整,时针与分针夹角为$9×30^{\circ}=270^{\circ}$。
40分钟内,时针走了$40×0.5^{\circ}=20^{\circ}$,分针走了$40×6^{\circ}=240^{\circ}$。
9时40分,时针位置为$270^{\circ}+20^{\circ}=290^{\circ}$,分针位置为$240^{\circ}$。
夹角为$|290^{\circ}-240^{\circ}|=50^{\circ}$。
$50^{\circ}$
10. 如图,∠BOC= 2∠AOB,OD平分∠AOC,∠BOD= 14°.求∠AOB的度数.
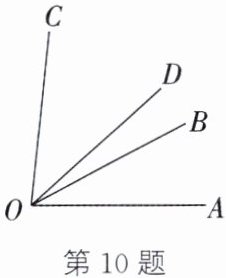

答案:设$\angle AOB=x$,则$\angle BOC=2x$。所以$\angle AOC=\angle AOB+\angle BOC=3x$。因为$OD$平分$\angle AOC$,所以$\angle AOD=\angle COD$。因为$\angle BOD=14^{\circ}$,所以$\angle AOD=\angle AOB+\angle BOD=x+14^{\circ}$,$\angle COD=\angle BOC-\angle BOD=2x-14^{\circ}$。所以$x+14^{\circ}=2x-14^{\circ}$,解得$x=28^{\circ}$。所以$\angle AOB=28^{\circ}$
解析:
设∠AOB = x,则∠BOC = 2x。
∠AOC = ∠AOB + ∠BOC = x + 2x = 3x。
因为OD平分∠AOC,所以∠AOD = ∠COD = $\frac{1}{2}$∠AOC = $\frac{3}{2}x$。
又因为∠AOD = ∠AOB + ∠BOD,∠BOD = 14°,
所以$\frac{3}{2}x = x + 14°$。
解得x = 28°。
故∠AOB = 28°。
∠AOC = ∠AOB + ∠BOC = x + 2x = 3x。
因为OD平分∠AOC,所以∠AOD = ∠COD = $\frac{1}{2}$∠AOC = $\frac{3}{2}x$。
又因为∠AOD = ∠AOB + ∠BOD,∠BOD = 14°,
所以$\frac{3}{2}x = x + 14°$。
解得x = 28°。
故∠AOB = 28°。
11. (分类讨论思想)已知线段AB= 8cm,C是直线AB上的一点,BC= 2cm.若M是线段AB的中点,N是线段BC的中点,则线段MN的长为 (
A.5cm
B.5cm或3cm
C.7cm或3cm
D.7cm
B
)A.5cm
B.5cm或3cm
C.7cm或3cm
D.7cm
答案:B
解析:
解:
情况1:点C在线段AB上
∵M是AB中点,AB=8cm,∴MB=AB/2=4cm。
∵N是BC中点,BC=2cm,∴NB=BC/2=1cm。
∴MN=MB-NB=4-1=3cm。
情况2:点C在线段AB延长线上
∵M是AB中点,AB=8cm,∴MB=AB/2=4cm。
∵N是BC中点,BC=2cm,∴NB=BC/2=1cm。
∴MN=MB+NB=4+1=5cm。
综上,MN的长为5cm或3cm。
答案:B
情况1:点C在线段AB上
∵M是AB中点,AB=8cm,∴MB=AB/2=4cm。
∵N是BC中点,BC=2cm,∴NB=BC/2=1cm。
∴MN=MB-NB=4-1=3cm。
情况2:点C在线段AB延长线上
∵M是AB中点,AB=8cm,∴MB=AB/2=4cm。
∵N是BC中点,BC=2cm,∴NB=BC/2=1cm。
∴MN=MB+NB=4+1=5cm。
综上,MN的长为5cm或3cm。
答案:B
12. (2023·南通期末)如图,∠AOB= ∠COD= ∠EOF= 90°,则∠1,∠2,∠3之间的数量关系为 (

A.∠1+∠2+∠3= 90°
B.∠1+∠2-∠3= 90°
C.∠2+∠3-∠1= 90°
D.∠1-∠2+∠3= 90°
D
)
A.∠1+∠2+∠3= 90°
B.∠1+∠2-∠3= 90°
C.∠2+∠3-∠1= 90°
D.∠1-∠2+∠3= 90°
答案:D
解析:
解:设∠AOC = x,∠COB = y,∠BOE = z,∠EOD = w。
由∠AOB = 90°,得 x + y = 90°;
由∠COD = 90°,得 y + z + w = 90°;
由∠EOF = 90°,得 w + ∠1 = 90°,即 w = 90° - ∠1。
又∠2 = z,∠3 = x。
将 w = 90° - ∠1 代入 y + z + w = 90°,得 y + ∠2 + 90° - ∠1 = 90°,即 y + ∠2 = ∠1。
由 x + y = 90°,得 y = 90° - x = 90° - ∠3。
代入 y + ∠2 = ∠1,得 90° - ∠3 + ∠2 = ∠1,整理得∠1 - ∠2 + ∠3 = 90°。
答案:D
由∠AOB = 90°,得 x + y = 90°;
由∠COD = 90°,得 y + z + w = 90°;
由∠EOF = 90°,得 w + ∠1 = 90°,即 w = 90° - ∠1。
又∠2 = z,∠3 = x。
将 w = 90° - ∠1 代入 y + z + w = 90°,得 y + ∠2 + 90° - ∠1 = 90°,即 y + ∠2 = ∠1。
由 x + y = 90°,得 y = 90° - x = 90° - ∠3。
代入 y + ∠2 = ∠1,得 90° - ∠3 + ∠2 = ∠1,整理得∠1 - ∠2 + ∠3 = 90°。
答案:D
13. 有两根木条,一根长10cm,另一根长8cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为
1或9
cm.答案:1或9
解析:
解:
情况一:两根木条同向放置,中点距离为$\frac{10}{2} - \frac{8}{2} = 5 - 4 = 1$cm;
情况二:两根木条反向放置,中点距离为$\frac{10}{2} + \frac{8}{2} = 5 + 4 = 9$cm。
1或9
情况一:两根木条同向放置,中点距离为$\frac{10}{2} - \frac{8}{2} = 5 - 4 = 1$cm;
情况二:两根木条反向放置,中点距离为$\frac{10}{2} + \frac{8}{2} = 5 + 4 = 9$cm。
1或9
14. 若一点在由两条具有公共端点的线段组成的一条折线上,且把这条折线分成长度相等的两部分,则把这一点叫作这条折线的“折中点”.如图,P即为折线M-O-N的“折中点”.若在折线A-O-B中,C是它的“折中点”,且OB= 8,OC= 3,则OA=
2或14
.答案:2或14
解析:
解:情况一:点C在OA上。
折线A-O-B的总长度为OA + OB = OA + 8。
因为C是折中点,所以AC = 1/2(OA + 8)。
又因为AC = OA - OC = OA - 3,
所以OA - 3 = 1/2(OA + 8),
解得OA = 14。
情况二:点C在OB上。
折线A-O-B的总长度为OA + OB = OA + 8。
因为C是折中点,所以AC = 1/2(OA + 8)。
又因为AC = OA + OC = OA + 3,
所以OA + 3 = 1/2(OA + 8),
解得OA = 2。
综上,OA = 2或14。
折线A-O-B的总长度为OA + OB = OA + 8。
因为C是折中点,所以AC = 1/2(OA + 8)。
又因为AC = OA - OC = OA - 3,
所以OA - 3 = 1/2(OA + 8),
解得OA = 14。
情况二:点C在OB上。
折线A-O-B的总长度为OA + OB = OA + 8。
因为C是折中点,所以AC = 1/2(OA + 8)。
又因为AC = OA + OC = OA + 3,
所以OA + 3 = 1/2(OA + 8),
解得OA = 2。
综上,OA = 2或14。
15. 若∠α与∠β互为余角,且∠α= 33°7'8'',则∠β的补角的度数为
$123^{\circ}7'8''$
.答案:$123^{\circ}7'8''$
解析:
解:因为∠α与∠β互为余角,所以∠α + ∠β = 90°。
∠β = 90° - ∠α = 90° - 33°7'8'' = 56°52'52''。
∠β的补角 = 180° - ∠β = 180° - 56°52'52'' = 123°7'8''。
123°7'8''
∠β = 90° - ∠α = 90° - 33°7'8'' = 56°52'52''。
∠β的补角 = 180° - ∠β = 180° - 56°52'52'' = 123°7'8''。
123°7'8''
16. 如图所示为由6个相同的正方体组成的立体图形,试分别画出从前面、左面、上面看它得到的平面图形.


答案:
如图所示

如图所示
