17. 如图,货轮O在航行过程中,发现灯塔A在它的南偏东60°方向上,同时,在它的北偏西30°方向上发现了客轮B,西北方向上又发现了海岛C.
(1) 仿照表示灯塔A方向的方法,在图中画出表示客轮B和海岛C方向的射线;
(2) 求∠BOC和∠AOB的度数.
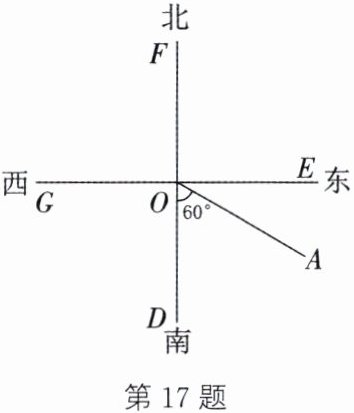
(1) 仿照表示灯塔A方向的方法,在图中画出表示客轮B和海岛C方向的射线;
(2) 求∠BOC和∠AOB的度数.

答案:
(1)如图所示 (2)由题意,得$\angle AOD=60^{\circ}$,$\angle COF=45^{\circ}$,$\angle BOF=30^{\circ}$,所以$\angle BOC=\angle COF-\angle BOF=45^{\circ}-30^{\circ}=15^{\circ}$。因为$\angle AOE=90^{\circ}-\angle AOD=90^{\circ}-60^{\circ}=30^{\circ}$,所以$\angle AOB=\angle BOF+\angle FOE+\angle AOE=30^{\circ}+90^{\circ}+30^{\circ}=150^{\circ}$
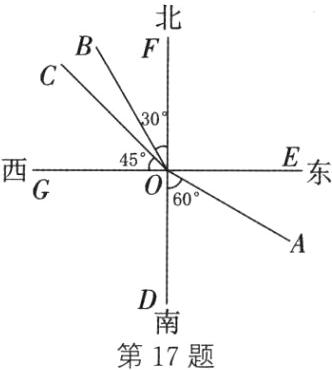
(1)如图所示 (2)由题意,得$\angle AOD=60^{\circ}$,$\angle COF=45^{\circ}$,$\angle BOF=30^{\circ}$,所以$\angle BOC=\angle COF-\angle BOF=45^{\circ}-30^{\circ}=15^{\circ}$。因为$\angle AOE=90^{\circ}-\angle AOD=90^{\circ}-60^{\circ}=30^{\circ}$,所以$\angle AOB=\angle BOF+\angle FOE+\angle AOE=30^{\circ}+90^{\circ}+30^{\circ}=150^{\circ}$

18. (2025·南通期末)如图,E是线段AB的中点,C是线段EB上一点,且EC:CB= 1:3.
(1) 设EC= x,则AE=
(2) 若AC= 10,F为CB的中点,求EF的长.

(1) 设EC= x,则AE=
4x
(用含x的代数式表示);(2) 若AC= 10,F为CB的中点,求EF的长.
由(1)得,$EC:AE=1:4$。因为$AE+EC=AC=10$,所以$AE=\frac{4}{1+4}AC=8$,$EC=\frac{1}{1+4}AC=2$。因为$EC:CB=1:3$,所以$BC=3EC=6$。因为$F$为$CB$的中点,所以$CF=\frac{1}{2}BC=3$。所以$EF=EC+CF=2+3=5$

答案:(1)$4x$ (2)由(1)得,$EC:AE=1:4$。因为$AE+EC=AC=10$,所以$AE=\frac{4}{1+4}AC=8$,$EC=\frac{1}{1+4}AC=2$。因为$EC:CB=1:3$,所以$BC=3EC=6$。因为$F$为$CB$的中点,所以$CF=\frac{1}{2}BC=3$。所以$EF=EC+CF=2+3=5$
解析:
(1) $4x$
(2) 解:由(1)得 $EC = x$,$AE = 4x$。
因为 $AC = AE + EC = 10$,所以 $4x + x = 10$,解得 $x = 2$,即 $EC = 2$。
因为 $EC:CB = 1:3$,所以 $CB = 3EC = 3×2 = 6$。
因为 $F$ 为 $CB$ 的中点,所以 $CF = \frac{1}{2}CB = \frac{1}{2}×6 = 3$。
所以 $EF = EC + CF = 2 + 3 = 5$。
答:$EF$ 的长为 $5$。
(2) 解:由(1)得 $EC = x$,$AE = 4x$。
因为 $AC = AE + EC = 10$,所以 $4x + x = 10$,解得 $x = 2$,即 $EC = 2$。
因为 $EC:CB = 1:3$,所以 $CB = 3EC = 3×2 = 6$。
因为 $F$ 为 $CB$ 的中点,所以 $CF = \frac{1}{2}CB = \frac{1}{2}×6 = 3$。
所以 $EF = EC + CF = 2 + 3 = 5$。
答:$EF$ 的长为 $5$。
19. 已知∠AOB与∠COD共顶点O,∠AOB= α,∠COD= β.
(1) 如图①,点A,O,C在一条直线上.若α= 60°,β= 30°,OM为∠AOD的平分线,ON为∠COB的平分线,求∠MON的度数.
(2) 若α= 2β,∠AOB,∠COD绕点O运动到如图②所示的位置,OE为∠BOD的平分线,用等式表示∠AOD与∠COE之间的数量关系,并说明理由.

(1) 如图①,点A,O,C在一条直线上.若α= 60°,β= 30°,OM为∠AOD的平分线,ON为∠COB的平分线,求∠MON的度数.
(2) 若α= 2β,∠AOB,∠COD绕点O运动到如图②所示的位置,OE为∠BOD的平分线,用等式表示∠AOD与∠COE之间的数量关系,并说明理由.

答案:(1)因为$\angle COD=30^{\circ}$,所以$\angle AOD=180^{\circ}-\angle COD=180^{\circ}-30^{\circ}=150^{\circ}$。因为$OM$为$\angle AOD$的平分线,所以$\angle AOM=\frac{1}{2}\angle AOD=75^{\circ}$。因为$\angle AOB=60^{\circ}$,所以$\angle COB=180^{\circ}-\angle AOB=180^{\circ}-60^{\circ}=120^{\circ}$。因为$ON$为$\angle COB$的平分线,所以$\angle CON=\frac{1}{2}\angle COB=60^{\circ}$。所以$\angle MON=180^{\circ}-\angle AOM-\angle CON=180^{\circ}-75^{\circ}-60^{\circ}=45^{\circ}$ (2)$\angle AOD=2\angle COE$ 理由:因为$OE$为$\angle BOD$的平分线,所以$\angle DOE=\frac{1}{2}\angle BOD$。因为$\angle BOD=\angle AOB+\angle AOD=\angle AOB+\angle COD-\angle AOC=\alpha+\beta-\angle AOC=2\beta+\beta-\angle AOC=3\beta-\angle AOC$,所以$\angle DOE=\frac{3}{2}\beta-\frac{1}{2}\angle AOC$。所以$\angle COE=\angle DOE-\angle COD=\frac{3}{2}\beta-\frac{1}{2}\angle AOC-\beta=\frac{1}{2}(\beta-\angle AOC)$。因为$\angle AOD=\angle BOD-\angle AOB=3\beta-\angle AOC-2\beta=\beta-\angle AOC$,所以$\angle AOD=2\angle COE$。
解析:
(1)解:因为∠COD=30°,点A,O,C在一条直线上,
所以∠AOD=180°-∠COD=180°-30°=150°。
因为OM为∠AOD的平分线,
所以∠AOM=1/2∠AOD=75°。
因为∠AOB=60°,
所以∠COB=180°-∠AOB=180°-60°=120°。
因为ON为∠COB的平分线,
所以∠CON=1/2∠COB=60°。
所以∠MON=180°-∠AOM-∠CON=180°-75°-60°=45°。
(2)∠AOD=2∠COE。
理由:因为OE为∠BOD的平分线,
所以∠DOE=1/2∠BOD。
因为∠AOB=α=2β,∠COD=β,
所以∠BOD=∠AOB+∠AOD=α+∠AOD=2β+∠AOD,
又因为∠BOD=∠COD+∠BOC=β+∠BOC,
所以∠AOD=∠BOC-β。
因为∠COE=∠BOE-∠BOC=1/2∠BOD-∠BOC=1/2(β+∠BOC)-∠BOC=1/2β-1/2∠BOC=1/2(β-∠BOC)。
又因为∠AOD=∠BOC-β=-(β-∠BOC),
所以∠AOD=2∠COE。
所以∠AOD=180°-∠COD=180°-30°=150°。
因为OM为∠AOD的平分线,
所以∠AOM=1/2∠AOD=75°。
因为∠AOB=60°,
所以∠COB=180°-∠AOB=180°-60°=120°。
因为ON为∠COB的平分线,
所以∠CON=1/2∠COB=60°。
所以∠MON=180°-∠AOM-∠CON=180°-75°-60°=45°。
(2)∠AOD=2∠COE。
理由:因为OE为∠BOD的平分线,
所以∠DOE=1/2∠BOD。
因为∠AOB=α=2β,∠COD=β,
所以∠BOD=∠AOB+∠AOD=α+∠AOD=2β+∠AOD,
又因为∠BOD=∠COD+∠BOC=β+∠BOC,
所以∠AOD=∠BOC-β。
因为∠COE=∠BOE-∠BOC=1/2∠BOD-∠BOC=1/2(β+∠BOC)-∠BOC=1/2β-1/2∠BOC=1/2(β-∠BOC)。
又因为∠AOD=∠BOC-β=-(β-∠BOC),
所以∠AOD=2∠COE。