1. 早在两千多年前,我国就有了正负数的概念. 在当时我国的商业活动中,以余钱为正,以亏钱为负,如果余钱5文记为+5文,那么亏钱3文记为 (
A.-3文
B.+3文
C.-5文
D.+5文
A
)A.-3文
B.+3文
C.-5文
D.+5文
答案:A
解析:
余钱为正,亏钱为负,亏钱3文记为-3文。
答案:A
答案:A
2. 在生产图纸上通常用$\Phi 300_{-0.5}^{+0.2}$来表示轴的加工要求,这里$\Phi 300$表示直径是300mm,$\Phi 300_{-0.5}^{+0.2}是指直径在(300 - 0.5)mm到(300 + 0.2)mm$之间的产品都属于合格产品. 现加工一批轴,尺寸要求是$\Phi 45_{-0.3}^{+0.2}$,则下列直径所对应的产品合格的是 (
A.44.6mm
B.44.8mm
C.45.3mm
D.45.5mm
B
)A.44.6mm
B.44.8mm
C.45.3mm
D.45.5mm
答案:B
解析:
解:由题意可知,轴的合格直径范围为:
$45 - 0.3 = 44.7$(mm)到$45 + 0.2 = 45.2$(mm)之间。
即合格范围是44.7mm~45.2mm。
选项中只有44.8mm在此范围内。
B
$45 - 0.3 = 44.7$(mm)到$45 + 0.2 = 45.2$(mm)之间。
即合格范围是44.7mm~45.2mm。
选项中只有44.8mm在此范围内。
B
3. 一辆汽车向南行驶5千米,再向南行驶-5千米,结果是 (
A.向南行驶10千米
B.向北行驶5千米
C.回到原地
D.向北行驶10千米
C
)A.向南行驶10千米
B.向北行驶5千米
C.回到原地
D.向北行驶10千米
答案:C
解析:
解:设向南为正方向。
第一次行驶:+5千米
第二次行驶:-5千米
总路程:+5 + (-5) = 0千米
结果是回到原地。
答案:C
第一次行驶:+5千米
第二次行驶:-5千米
总路程:+5 + (-5) = 0千米
结果是回到原地。
答案:C
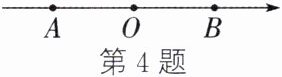
4. 如图,数轴上A,B两点在原点两侧,且$OA = OB$. 若$AB = 4$,则点A表示的数是 (
A.4
B.-4
C.2
D.-2
D
) 
A.4
B.-4
C.2
D.-2
答案:D
解析:
解:设点A表示的数为a,点B表示的数为b。
因为A,B两点在原点两侧,且OA=OB,
所以a=-b,且a<0,b>0。
因为AB=4,
所以b - a = 4。
将a=-b代入b - a = 4,得b - (-b)=4,
即2b=4,解得b=2。
所以a=-b=-2。
答案:D
因为A,B两点在原点两侧,且OA=OB,
所以a=-b,且a<0,b>0。
因为AB=4,
所以b - a = 4。
将a=-b代入b - a = 4,得b - (-b)=4,
即2b=4,解得b=2。
所以a=-b=-2。
答案:D
5. 下列各数中,最小的是 (
A.2
B.0
C.1.5
D.-3
D
)A.2
B.0
C.1.5
D.-3
答案:D
解析:
解:将各数按从小到大排列:-3 < 0 < 1.5 < 2,最小的数是-3。
答案:D
答案:D
6. 在$-(-\frac{1}{4}),-1,0,-|-4|,-(+3),+(-1\frac{1}{2}),-|0 - 8|$这几个有理数中,负数的个数是 (
A.5
B.4
C.3
D.2
A
)A.5
B.4
C.3
D.2
答案:A
解析:
解:$-(-\frac{1}{4})=\frac{1}{4}$,$-|-4|=-4$,$-(+3)=-3$,$+(-1\frac{1}{2})=-1\frac{1}{2}$,$-|0 - 8|=-8$。
负数有:$-1$,$-|-4|$,$-(+3)$,$+(-1\frac{1}{2})$,$-|0 - 8|$,共5个。
A
负数有:$-1$,$-|-4|$,$-(+3)$,$+(-1\frac{1}{2})$,$-|0 - 8|$,共5个。
A
7. 数轴上某一个点表示的数为a,比a小2的数用b表示,那么$|a|+|b|$的最小值为 (
A.0
B.1
C.2
D.3
C
)A.0
B.1
C.2
D.3
答案:C
解析:
解:由题意得,$b = a - 2$,则$|a| + |b| = |a| + |a - 2|$。
分情况讨论:
1. 当$a \leq 0$时,$|a| + |a - 2| = -a + (2 - a) = 2 - 2a$,此时随着$a$增大,值减小,当$a = 0$时,值为$2$。
2. 当$0 < a < 2$时,$|a| + |a - 2| = a + (2 - a) = 2$。
3. 当$a \geq 2$时,$|a| + |a - 2| = a + (a - 2) = 2a - 2$,此时随着$a$增大,值增大,当$a = 2$时,值为$2$。
综上,$|a| + |b|$的最小值为$2$。
答案:C
分情况讨论:
1. 当$a \leq 0$时,$|a| + |a - 2| = -a + (2 - a) = 2 - 2a$,此时随着$a$增大,值减小,当$a = 0$时,值为$2$。
2. 当$0 < a < 2$时,$|a| + |a - 2| = a + (2 - a) = 2$。
3. 当$a \geq 2$时,$|a| + |a - 2| = a + (a - 2) = 2a - 2$,此时随着$a$增大,值增大,当$a = 2$时,值为$2$。
综上,$|a| + |b|$的最小值为$2$。
答案:C
8. 商店一周共亏损840元,平均每天的利润是
-120
元(记盈利额为正数,亏损额为负数).答案:$-120$
解析:
一周有7天,总亏损840元,记亏损额为负数,所以总利润为-840元。
平均每天的利润 = 总利润 ÷ 天数 = -840 ÷ 7 = -120(元)
-120
平均每天的利润 = 总利润 ÷ 天数 = -840 ÷ 7 = -120(元)
-120
9. 通常把水结冰时的温度规定为$0^{\circ}C$,那么比水结冰时的温度低$5^{\circ}C$,应记作
$-5$
$^{\circ}C$.答案:$-5$
10. 生活中常有用正负数表示范围的情形,例如某种食品的说明书上标明保存温度是$(25\pm 2)^{\circ}C$,请你写出一个适合该食品保存的温度为
25
$^{\circ}C$.答案:答案不唯一,如 25
11. 比较大小:$-\frac{2}{3}$
<
$-\frac{1}{2}$(填“>”“<”或“=”).答案:$<$
解析:
解:比较两个负数的大小,先比较它们的绝对值。
$\left| -\frac{2}{3} \right| = \frac{2}{3} = \frac{4}{6}$,$\left| -\frac{1}{2} \right| = \frac{1}{2} = \frac{3}{6}$。
因为$\frac{4}{6}>\frac{3}{6}$,所以$-\frac{2}{3}<-\frac{1}{2}$。
<
$\left| -\frac{2}{3} \right| = \frac{2}{3} = \frac{4}{6}$,$\left| -\frac{1}{2} \right| = \frac{1}{2} = \frac{3}{6}$。
因为$\frac{4}{6}>\frac{3}{6}$,所以$-\frac{2}{3}<-\frac{1}{2}$。
<
12. 若$|2a - 1| - 5 = 0$,则$a = $
3 或 $-2$
.答案:3 或 $-2$
解析:
解:|2a - 1| - 5 = 0
|2a - 1| = 5
2a - 1 = 5 或 2a - 1 = -5
当2a - 1 = 5时,2a = 6,a = 3
当2a - 1 = -5时,2a = -4,a = -2
a = 3 或 -2
|2a - 1| = 5
2a - 1 = 5 或 2a - 1 = -5
当2a - 1 = 5时,2a = 6,a = 3
当2a - 1 = -5时,2a = -4,a = -2
a = 3 或 -2
13. 已知数轴上点A表示的数是$-1\frac{1}{2}$. 若数轴上点P在点A的右侧,且到点A的距离等于$1\frac{1}{3}$,则点P表示的数是
$-\frac{1}{6}$
.答案:$-\frac{1}{6}$
解析:
解:点A表示的数是$-1\frac{1}{2}=-\frac{3}{2}$,点P在点A右侧,距离为$1\frac{1}{3}=\frac{4}{3}$。
点P表示的数为:$-\frac{3}{2}+\frac{4}{3}=-\frac{9}{6}+\frac{8}{6}=-\frac{1}{6}$
$-\frac{1}{6}$
点P表示的数为:$-\frac{3}{2}+\frac{4}{3}=-\frac{9}{6}+\frac{8}{6}=-\frac{1}{6}$
$-\frac{1}{6}$
14. 如图,点A,B在数轴上表示的数分别为-1,2. 若B是AC的中点,则点C表示的数是
5
.答案:5
解析:
解:设点C表示的数是x。
因为B是AC的中点,所以点B表示的数是点A和点C表示的数的平均数,即
$\frac{-1 + x}{2} = 2$
解得
$-1 + x = 4 \implies x = 5$
5
因为B是AC的中点,所以点B表示的数是点A和点C表示的数的平均数,即
$\frac{-1 + x}{2} = 2$
解得
$-1 + x = 4 \implies x = 5$
5
整数:…{
正数:…{
负有理数:…{
①③④⑥
}; 正数:…{
②③⑥⑧
}; 负有理数:…{
④⑤⑦
}.答案:①③④⑥ ②③⑥⑧ ④⑤⑦
解析:
整数:{①③④⑥};
正数:{②③⑥⑧};
负有理数:{④⑤⑦}.
正数:{②③⑥⑧};
负有理数:{④⑤⑦}.