11. 定义:若一个一元一次方程的一次项系数与常数项的差刚好是这个方程的解的$2$倍,则称这个方程为“妙解方程”. 如:方程$3 x + 9 = 0$中,$3 - 9 = - 6$,方程的解为$x = - 3$,$- 6 = 2 × ( - 3 )$,则方程$3 x + 9 = 0$为“妙解方程”. 请根据上述定义解答:若关于$x的一元一次方程3 ( x - a ) - 2 ( 1 + x ) = 0$是“妙解方程”,则$a$的值为
$-\frac{1}{3}$
.答案:$-\frac{1}{3}$
解析:
解:解方程$3(x - a) - 2(1 + x) = 0$,
去括号得:$3x - 3a - 2 - 2x = 0$,
合并同类项得:$x - 3a - 2 = 0$,
移项得:$x = 3a + 2$。
原方程化为一般形式为$x - (3a + 2) = 0$,其中一次项系数为$1$,常数项为$-(3a + 2)$。
根据“妙解方程”定义,一次项系数与常数项的差是解的$2$倍,可得:
$1 - [-(3a + 2)] = 2(3a + 2)$,
化简得:$1 + 3a + 2 = 6a + 4$,
$3a + 3 = 6a + 4$,
移项得:$3a - 6a = 4 - 3$,
$-3a = 1$,
解得:$a = -\frac{1}{3}$。
$-\frac{1}{3}$
去括号得:$3x - 3a - 2 - 2x = 0$,
合并同类项得:$x - 3a - 2 = 0$,
移项得:$x = 3a + 2$。
原方程化为一般形式为$x - (3a + 2) = 0$,其中一次项系数为$1$,常数项为$-(3a + 2)$。
根据“妙解方程”定义,一次项系数与常数项的差是解的$2$倍,可得:
$1 - [-(3a + 2)] = 2(3a + 2)$,
化简得:$1 + 3a + 2 = 6a + 4$,
$3a + 3 = 6a + 4$,
移项得:$3a - 6a = 4 - 3$,
$-3a = 1$,
解得:$a = -\frac{1}{3}$。
$-\frac{1}{3}$
12. 任何一个无限循环小数都可以写成分数的形式,应该怎样写呢? 我们以无限循环小数$0.\dot { 7 }$为例进行说明:设$0.\dot { 7 } = x$,由$0.\dot { 7 } = 0.7777 …$,可知$10 x = 7.7777 …$,所以$10 x - x = 7$,解得$x = \frac { 7 } { 9 }$.所以$0.\dot { 7 } = \frac { 7 } { 9 }$. 将$0.\dot { 3 } \dot { 6 }$写成分数的形式为
$\frac{4}{11}$
.答案:$\frac{4}{11}$ 解析:设 $0.\dot{3}\dot{6}=x$,则 $100x=36.\dot{3}\dot{6}$。所以 $100x - x = 36$,解得 $x=\frac{4}{11}$。所以 $0.\dot{3}\dot{6}=\frac{4}{11}$。
解析:
设$0.\dot{3}\dot{6}=x$,则$100x = 36.\dot{3}\dot{6}$。
$100x - x = 36.\dot{3}\dot{6} - 0.\dot{3}\dot{6}$
$99x = 36$
解得$x = \frac{36}{99} = \frac{4}{11}$
所以$0.\dot{3}\dot{6} = \frac{4}{11}$
$\frac{4}{11}$
$100x - x = 36.\dot{3}\dot{6} - 0.\dot{3}\dot{6}$
$99x = 36$
解得$x = \frac{36}{99} = \frac{4}{11}$
所以$0.\dot{3}\dot{6} = \frac{4}{11}$
$\frac{4}{11}$
13. 解下面的方程:
(1)$10 - 4 ( x + 3 ) = 2 ( x - 1 )$;
(2)$\frac { 1.5 x - 1 } { 3 } - \frac { x } { 0.5 } = 0.5$.
(1)$10 - 4 ( x + 3 ) = 2 ( x - 1 )$;
(2)$\frac { 1.5 x - 1 } { 3 } - \frac { x } { 0.5 } = 0.5$.
答案:(1)$x = 0$ (2)$x = -\frac{5}{9}$
解析:
(1)解:$10 - 4(x + 3) = 2(x - 1)$
$10 - 4x - 12 = 2x - 2$
$-4x - 2 = 2x - 2$
$-4x - 2x = -2 + 2$
$-6x = 0$
$x = 0$
(2)解:$\frac{1.5x - 1}{3} - \frac{x}{0.5} = 0.5$
$\frac{3x - 2}{6} - 2x = 0.5$
$3x - 2 - 12x = 3$
$-9x = 5$
$x = -\frac{5}{9}$
$10 - 4x - 12 = 2x - 2$
$-4x - 2 = 2x - 2$
$-4x - 2x = -2 + 2$
$-6x = 0$
$x = 0$
(2)解:$\frac{1.5x - 1}{3} - \frac{x}{0.5} = 0.5$
$\frac{3x - 2}{6} - 2x = 0.5$
$3x - 2 - 12x = 3$
$-9x = 5$
$x = -\frac{5}{9}$
14. (2025·海门期末)如图,甲、乙两支登山队沿同一条路线同时向峰顶进发,甲队从距大本营$1$千米的一号营地出发,每小时行进$1.2$千米;乙队从距大本营$3$千米的二号营地出发,每小时行进$0.8$千米. 多长时间后,甲队在途中追上乙队?
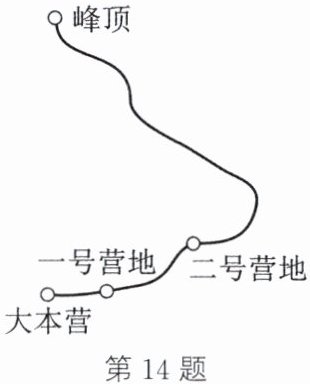

答案:设 $x$ 小时后,甲队在途中追上乙队。根据题意,得 $1.2x - 0.8x = 3 - 1$,解得 $x = 5$。所以 5 小时后,甲队在途中追上乙队
解析:
解:设$x$小时后,甲队在途中追上乙队。
根据题意,甲队行进的路程为$1.2x$千米,乙队行进的路程为$0.8x$千米。
甲队从一号营地出发,距大本营$1$千米;乙队从二号营地出发,距大本营$3$千米,所以乙队初始位置比甲队远$3 - 1 = 2$千米。当甲队追上乙队时,甲队比乙队多行进了$2$千米,可列方程:
$1.2x - 0.8x = 3 - 1$
化简得:$0.4x = 2$
解得:$x = 5$
答:$5$小时后,甲队在途中追上乙队。
根据题意,甲队行进的路程为$1.2x$千米,乙队行进的路程为$0.8x$千米。
甲队从一号营地出发,距大本营$1$千米;乙队从二号营地出发,距大本营$3$千米,所以乙队初始位置比甲队远$3 - 1 = 2$千米。当甲队追上乙队时,甲队比乙队多行进了$2$千米,可列方程:
$1.2x - 0.8x = 3 - 1$
化简得:$0.4x = 2$
解得:$x = 5$
答:$5$小时后,甲队在途中追上乙队。
15. 某工厂有$28名工人生产A零件和B$零件,每人每天可生产$A零件18个或B零件12$个(每人每天只能生产一种零件),一个$A零件配两个B$零件,且每天生产的$A零件和B$零件恰好配套. 工厂将零件批发给商场时,每个$A零件可获利10$元,每个$B零件可获利5$元.
(1)该工厂有多少名工人生产$A$零件?
(2)因市场需求,该工厂每天要多生产一部分$A$零件供商场零售使用,现从生产$B零件的工人中调出多少名工人生产A$零件,才能使每日生产的零件总获利比调动前多$600$元?
(1)该工厂有多少名工人生产$A$零件?
(2)因市场需求,该工厂每天要多生产一部分$A$零件供商场零售使用,现从生产$B零件的工人中调出多少名工人生产A$零件,才能使每日生产的零件总获利比调动前多$600$元?
答案:(1)设该工厂有 $x$ 名工人生产 A 零件。根据题意,得 $2×18x = 12(28 - x)$,解得 $x = 7$,则 $28 - x = 21$。所以该工厂有 7 名工人生产 A 零件 (2)设从生产 B 零件的工人中调出 $y$ 名工人生产 A 零件。根据题意,得 $10×18(7 + y) + 5×12(21 - y) - (7×10×18 + 21×5×12) = 600$,解得 $y = 5$。所以从生产 B 零件的工人中调出 5 名工人生产 A 零件
解析:
(1)设该工厂有$x$名工人生产$A$零件,则有$(28 - x)$名工人生产$B$零件。根据题意,得$2×18x = 12(28 - x)$,解得$x = 7$。答:该工厂有$7$名工人生产$A$零件。
(2)设从生产$B$零件的工人中调出$y$名工人生产$A$零件。调动前总获利为$7×18×10 + 21×12×5$,调动后生产$A$零件的工人有$(7 + y)$名,生产$B$零件的工人有$(21 - y)$名,总获利为$18(7 + y)×10 + 12(21 - y)×5$。根据题意,得$[18(7 + y)×10 + 12(21 - y)×5] - [7×18×10 + 21×12×5] = 600$,解得$y = 5$。答:从生产$B$零件的工人中调出$5$名工人生产$A$零件。
(2)设从生产$B$零件的工人中调出$y$名工人生产$A$零件。调动前总获利为$7×18×10 + 21×12×5$,调动后生产$A$零件的工人有$(7 + y)$名,生产$B$零件的工人有$(21 - y)$名,总获利为$18(7 + y)×10 + 12(21 - y)×5$。根据题意,得$[18(7 + y)×10 + 12(21 - y)×5] - [7×18×10 + 21×12×5] = 600$,解得$y = 5$。答:从生产$B$零件的工人中调出$5$名工人生产$A$零件。