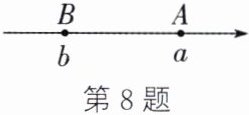
8. (数形结合思想)如图,数轴上A,B两点所表示的数分别为a,b,且$a+b>0,ab<0$,则原点的位置在 (
A.点A的右边
B.点B的左边
C.A,B两点之间,且靠近点A
D.A,B两点之间,且靠近点B
D
)
A.点A的右边
B.点B的左边
C.A,B两点之间,且靠近点A
D.A,B两点之间,且靠近点B
答案:D
解析:
解:
∵ $ab < 0$,
∴ $a$、$b$异号。
由数轴知 $b < a$,
∴ $b < 0$,$a > 0$。
∵ $a + b > 0$,
∴ $|a| > |b|$。
∴原点在A、B两点之间,且靠近点B。
答案:D
∵ $ab < 0$,
∴ $a$、$b$异号。
由数轴知 $b < a$,
∴ $b < 0$,$a > 0$。
∵ $a + b > 0$,
∴ $|a| > |b|$。
∴原点在A、B两点之间,且靠近点B。
答案:D
9. 从5,-3,2,-4中任取两个数相乘,所得的积最小是 (
A.-6
B.8
C.-15
D.-20
D
)A.-6
B.8
C.-15
D.-20
答案:D
解析:
解:从5,-3,2,-4中任取两个数相乘,所有可能的积为:
5×(-3)=-15,
5×2=10,
5×(-4)=-20,
-3×2=-6,
-3×(-4)=12,
2×(-4)=-8,
比较这些积:-20<-15<-8<-6<10<12,
所以所得的积最小是-20。
答案:D
5×(-3)=-15,
5×2=10,
5×(-4)=-20,
-3×2=-6,
-3×(-4)=12,
2×(-4)=-8,
比较这些积:-20<-15<-8<-6<10<12,
所以所得的积最小是-20。
答案:D
10. (分类讨论思想)(1)若$|a|= 8,|b|= 2$,且$a+b>0$,则$ab= $
(2)若$|x|= 4,|y|= 7$,且$x-y>0$,则$xy= $
16或-16
;(2)若$|x|= 4,|y|= 7$,且$x-y>0$,则$xy= $
28或-28
.答案:(1) 16或-16 (2) 28或-28
解析:
(1)
∵|a|=8,|b|=2,
∴a=±8,b=±2。
∵a+b>0,
∴当a=8时,b=2或-2均满足;当a=-8时,b=±2均不满足。
∴a=8,b=2时,ab=16;a=8,b=-2时,ab=-16。
∴ab=16或-16。
(2)
∵|x|=4,|y|=7,
∴x=±4,y=±7。
∵x-y>0,即x>y,
∴当x=4时,y=-7满足;当x=-4时,y=-7满足;y=7时均不满足。
∴x=4,y=-7时,xy=-28;x=-4,y=-7时,xy=28。
∴xy=28或-28。
∵|a|=8,|b|=2,
∴a=±8,b=±2。
∵a+b>0,
∴当a=8时,b=2或-2均满足;当a=-8时,b=±2均不满足。
∴a=8,b=2时,ab=16;a=8,b=-2时,ab=-16。
∴ab=16或-16。
(2)
∵|x|=4,|y|=7,
∴x=±4,y=±7。
∵x-y>0,即x>y,
∴当x=4时,y=-7满足;当x=-4时,y=-7满足;y=7时均不满足。
∴x=4,y=-7时,xy=-28;x=-4,y=-7时,xy=28。
∴xy=28或-28。
11. 有理数a,b,c,d在数轴上的对应点的位置如图所示,用“>”或“<”填空:

(1)$ab$
(2)$ac$
(3)$(a+b)(c+d)$
(4)$(d-a)(b-c)$

(1)$ab$
>
0;(2)$ac$
<
0;(3)$(a+b)(c+d)$
<
0;(4)$(d-a)(b-c)$
<
0.答案:(1) > (2) < (3) < (4) <
解析:
(1) 由数轴可知,$a$在$-3$与$-2$之间,为负数;$b$在$-1$与$0$之间,为负数。两负数相乘得正数,所以$ab>0$。
(2) $a$为负数,$c$在$1$与$2$之间,为正数。异号相乘得负数,所以$ac<0$。
(3) $a$为负数,$b$为负数,两负数相加仍为负数,即$a + b<0$;$c$为正数,$d$在$2$与$3$之间,为正数,两正数相加为正数,即$c + d>0$。异号相乘得负数,所以$(a + b)(c + d)<0$。
(4) $d$为正数,$a$为负数,正数减负数得正数,即$d - a>0$;$b$为负数,$c$为正数,负数减正数得负数,即$b - c<0$。异号相乘得负数,所以$(d - a)(b - c)<0$。
(1)>
(2)<
(3)<
(4)<
(2) $a$为负数,$c$在$1$与$2$之间,为正数。异号相乘得负数,所以$ac<0$。
(3) $a$为负数,$b$为负数,两负数相加仍为负数,即$a + b<0$;$c$为正数,$d$在$2$与$3$之间,为正数,两正数相加为正数,即$c + d>0$。异号相乘得负数,所以$(a + b)(c + d)<0$。
(4) $d$为正数,$a$为负数,正数减负数得正数,即$d - a>0$;$b$为负数,$c$为正数,负数减正数得负数,即$b - c<0$。异号相乘得负数,所以$(d - a)(b - c)<0$。
(1)>
(2)<
(3)<
(4)<
12. 某数学小组的10名同学站成一列做报数游戏,规则:从前面第1名同学开始,每名同学依次报自己序号的倒数的2倍加1,第1名同学报$(\frac {2}{1}+1)$,第2名同学报$(\frac {2}{2}+1)$,第3名同学报$(\frac {2}{3}+1)$……这样得到的10个数的积为
13. 计算:
(1)$(-0.8)×(-\frac {7}{4})$
(2)$(-1\frac {3}{5})×(+3\frac {3}{4})$
(3)$(-4)×(-12)-(-5)×|-11|$
66
.13. 计算:
(1)$(-0.8)×(-\frac {7}{4})$
$\frac{7}{5}$
; (2)$(-1\frac {3}{5})×(+3\frac {3}{4})$
-6
;(3)$(-4)×(-12)-(-5)×|-11|$
103
.答案:12. 66 解析:第1名同学报的数是$\frac{2}{1}+1=\frac{3}{1}$,第2名同学报的数是$\frac{2}{2}+1=\frac{4}{2}$,第3名同学报的数是$\frac{2}{3}+1=\frac{5}{3}$,第4名同学报的数是$\frac{2}{4}+1=\frac{6}{4}$……第10名同学报的数是$\frac{2}{10}+1=\frac{12}{10}$,所以10个数的积为$\frac{3}{1}×\frac{4}{2}×\frac{5}{3}×\frac{6}{4}×…×\frac{12}{10}=\frac{11×12}{1×2}=66$。
13. 计算:
(1)$(-0.8)×(-\frac {7}{4})$;
(2)$(-1\frac {3}{5})×(+3\frac {3}{4})$;
(3)$(-4)×(-12)-(-5)×|-11|$.
(1)$(-0.8)×(-\frac {7}{4})$;
(2)$(-1\frac {3}{5})×(+3\frac {3}{4})$;
(3)$(-4)×(-12)-(-5)×|-11|$.
答案:1. (1)
解:$(-0.8)×(-\frac{7}{4})=\frac{4}{5}×\frac{7}{4}=\frac{7}{5}$。
2. (2)
解:$(-1\frac{3}{5})×(+3\frac{3}{4})=(-\frac{8}{5})×(\frac{15}{4})=-6$。
3. (3)
解:$(-4)×(-12)-(-5)×|-11|$
先计算乘法和绝对值:
$(-4)×(-12)=48$,$|-11| = 11$,$(-5)×|-11|=-5×11=-55$。
再计算减法:
原式$=48-(-55)=48 + 55=103$。
综上,(1)的结果为$\frac{7}{5}$;(2)的结果为$-6$;(3)的结果为$103$。
解:$(-0.8)×(-\frac{7}{4})=\frac{4}{5}×\frac{7}{4}=\frac{7}{5}$。
2. (2)
解:$(-1\frac{3}{5})×(+3\frac{3}{4})=(-\frac{8}{5})×(\frac{15}{4})=-6$。
3. (3)
解:$(-4)×(-12)-(-5)×|-11|$
先计算乘法和绝对值:
$(-4)×(-12)=48$,$|-11| = 11$,$(-5)×|-11|=-5×11=-55$。
再计算减法:
原式$=48-(-55)=48 + 55=103$。
综上,(1)的结果为$\frac{7}{5}$;(2)的结果为$-6$;(3)的结果为$103$。
14. (新考法·新定义题)规定一种新运算“*”:$a*b= (a+2)×2-b$,例如:$3*5= (3+2)×2-5= 10-5= 5$. 根据运算规律解决问题.
(1)求$7*(-3)$的值;
(2)$7*(-3)与(-3)*7$的值相等吗?
(1)求$7*(-3)$的值;
(2)$7*(-3)与(-3)*7$的值相等吗?
答案:(1) $7*(-3)=(7+2)×2-(-3)=21$ (2) 因为$(-3)*7=[(-3)+2]×2-7=-9$,所以$7*(-3)$与$(-3)*7$的值不相等
解析:
(1) $7*(-3)=(7+2)×2-(-3)=9×2+3=18+3=21$
(2) $(-3)*7=[(-3)+2]×2-7=(-1)×2-7=-2-7=-9$
因为$21\neq-9$,所以$7*(-3)$与$(-3)*7$的值不相等。
(2) $(-3)*7=[(-3)+2]×2-7=(-1)×2-7=-2-7=-9$
因为$21\neq-9$,所以$7*(-3)$与$(-3)*7$的值不相等。