1. (教材P93练习第1题变式)有下列式子:$\frac {1}{3}ab,\frac {a+b}{2},\frac {1}{x}+\frac {2}{y},x^{2}+x-3$.其中,多项式有 (
A.1个
B.2个
C.3个
D.4个
B
)A.1个
B.2个
C.3个
D.4个
答案:B
解析:
解:多项式是几个单项式的和。
$\frac{1}{3}ab$是单项式,不是多项式;
$\frac{a+b}{2}=\frac{a}{2}+\frac{b}{2}$,是两个单项式的和,是多项式;
$\frac{1}{x}+\frac{2}{y}$中分母含有字母,不是整式,不是多项式;
$x^2+x-3$是三个单项式的和,是多项式。
综上,多项式有2个。
答案:B
$\frac{1}{3}ab$是单项式,不是多项式;
$\frac{a+b}{2}=\frac{a}{2}+\frac{b}{2}$,是两个单项式的和,是多项式;
$\frac{1}{x}+\frac{2}{y}$中分母含有字母,不是整式,不是多项式;
$x^2+x-3$是三个单项式的和,是多项式。
综上,多项式有2个。
答案:B
2. (2024·海门期中)对于多项式$x^{2}y-3xy-4$,下列说法正确的是 (
A.二次项系数是3
B.常数项是4
C.次数是3
D.项数是2
C
)A.二次项系数是3
B.常数项是4
C.次数是3
D.项数是2
答案:C
解析:
解:多项式$x^{2}y - 3xy - 4$各项分析如下:
二次项为$-3xy$,系数是$-3$,A错误;
常数项是$-4$,B错误;
最高次项$x^{2}y$的次数为$2 + 1 = 3$,多项式次数是3,C正确;
该多项式有$x^{2}y$、$-3xy$、$-4$三项,项数是3,D错误。
答案:C
二次项为$-3xy$,系数是$-3$,A错误;
常数项是$-4$,B错误;
最高次项$x^{2}y$的次数为$2 + 1 = 3$,多项式次数是3,C正确;
该多项式有$x^{2}y$、$-3xy$、$-4$三项,项数是3,D错误。
答案:C
3. 若$3xy^{m}+(n+1)x$是关于x,y的四次二项式,则m,n的取值情况是 (
A.$m≠3,n≠-1$
B.$m= 3,n≠-1$
C.$m≠3,n= -1$
D.$m= 3,n≠1$
B
)A.$m≠3,n≠-1$
B.$m= 3,n≠-1$
C.$m≠3,n= -1$
D.$m= 3,n≠1$
答案:B
解析:
解:因为$3xy^{m}+(n+1)x$是关于$x$,$y$的四次二项式。
对于多项式的次数,是指多项式中次数最高的项的次数。在$3xy^{m}$中,$x$的次数是$1$,$y$的次数是$m$,所以该项的次数为$1 + m$。因为多项式是四次式,所以$1 + m = 4$,解得$m = 3$。
又因为多项式是二项式,所以式子中只能有两项,而$(n + 1)x$这一项不能为$0$,否则就变成一项了,即$n + 1 \neq 0$,解得$n \neq -1$。
综上,$m = 3$,$n \neq -1$,答案选 B。
对于多项式的次数,是指多项式中次数最高的项的次数。在$3xy^{m}$中,$x$的次数是$1$,$y$的次数是$m$,所以该项的次数为$1 + m$。因为多项式是四次式,所以$1 + m = 4$,解得$m = 3$。
又因为多项式是二项式,所以式子中只能有两项,而$(n + 1)x$这一项不能为$0$,否则就变成一项了,即$n + 1 \neq 0$,解得$n \neq -1$。
综上,$m = 3$,$n \neq -1$,答案选 B。
4. $-2a^{3}b+2a^{2}b-7a-9$的次数最高项是
$-2a^{3}b$
,一次项系数是$-7$
,常数项是$-9$
.答案:$-2a^{3}b$ $-7$ $-9$
5. (教材P100练习第4题变式)某地居民的生活用水收费标准如下:每月用水量不超过$12m^{3}$,每立方米a元,超过部分每立方米b元.若该地区某家庭上月用水量为$15m^{3}$,则应缴水费
$(12a + 3b)$
元,这是一个一
次二
项式.答案:$(12a + 3b)$ 一 二
解析:
应缴水费:$12a + (15 - 12)b = 12a + 3b$(元)
这是一个一次二项式。
$(12a + 3b)$ 一 二
这是一个一次二项式。
$(12a + 3b)$ 一 二
6. 已知多项式$-3x^{2}y^{m+1}+x^{3}y-3x^{4}-1$是五次四项式,且单项式$3x^{2n}y^{3-m}$与该多项式的次数相同.
(1)求m,n的值;
(2)当$x= -1,y= 1$时,求该多项式的值.
(1)求m,n的值;
(2)当$x= -1,y= 1$时,求该多项式的值.
答案:(1) 由题意,得 $2 + m + 1 = 5$,解得 $m = 2$。又因为单项式 $3x^{2n}y^{3 - m}$ 与该多项式的次数相同,所以 $2n + 3 - m = 5$,即 $2n + 3 - 2 = 5$,解得 $n = 2$ (2) 当 $x = -1$,$y = 1$ 时,原式 $= -3×1×1 + (-1)×1 - 3×1 - 1 = -8$
解析:
(1) 解:因为多项式$-3x^{2}y^{m+1}+x^{3}y-3x^{4}-1$是五次四项式,所以该多项式的最高次项的次数为$5$。各项次数依次为:$2 + m + 1$,$3 + 1 = 4$,$4$,$0$,则$2 + m + 1 = 5$,解得$m = 2$。
又因为单项式$3x^{2n}y^{3 - m}$与该多项式的次数相同,所以$2n + 3 - m = 5$,将$m = 2$代入得$2n + 3 - 2 = 5$,解得$n = 2$。
(2) 解:由(1)知$m = 2$,所以多项式为$-3x^{2}y^{3}+x^{3}y-3x^{4}-1$。
当$x = -1$,$y = 1$时,原式$= -3×(-1)^{2}×1^{3}+(-1)^{3}×1 - 3×(-1)^{4}-1$
$= -3×1×1 + (-1)×1 - 3×1 - 1$
$= -3 - 1 - 3 - 1 = -8$。
又因为单项式$3x^{2n}y^{3 - m}$与该多项式的次数相同,所以$2n + 3 - m = 5$,将$m = 2$代入得$2n + 3 - 2 = 5$,解得$n = 2$。
(2) 解:由(1)知$m = 2$,所以多项式为$-3x^{2}y^{3}+x^{3}y-3x^{4}-1$。
当$x = -1$,$y = 1$时,原式$= -3×(-1)^{2}×1^{3}+(-1)^{3}×1 - 3×(-1)^{4}-1$
$= -3×1×1 + (-1)×1 - 3×1 - 1$
$= -3 - 1 - 3 - 1 = -8$。
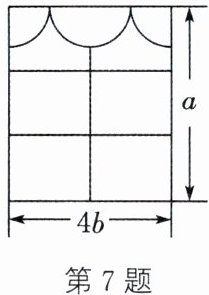
7. 小明房间的窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同).
(1)装饰物所占的面积是多少? 窗户中能射进阳光的部分的面积是多少(窗框的厚度忽略不计)?
(2)观察(1)中所得到的结果,它们是单项式还是多项式? 次数分别是多少?
(1)装饰物所占的面积是多少? 窗户中能射进阳光的部分的面积是多少(窗框的厚度忽略不计)?
(2)观察(1)中所得到的结果,它们是单项式还是多项式? 次数分别是多少?

答案:(1) 由题意知,四分之一圆与半圆的半径均为 $\frac{4b}{4} = b$,所以装饰物所占的面积是 $\pi b^{2}$,窗户中能射进阳光的部分的面积是 $4ab - \pi b^{2}$ (2) $\pi b^{2}$ 是单项式,次数是 2;$4ab - \pi b^{2}$ 是多项式,次数是 2
解析:
(1) 由题意知,四分之一圆与半圆的半径均为 $\frac{4b}{4} = b$。
装饰物面积:两个四分之一圆面积加一个半圆面积,即 $\frac{1}{4}\pi b^2 × 2 + \frac{1}{2}\pi b^2 = \pi b^2$。
窗户面积:$4b × a = 4ab$,能射进阳光的面积:$4ab - \pi b^2$。
(2) $\pi b^2$ 是单项式,次数是 2;$4ab - \pi b^2$ 是多项式,次数是 2。
装饰物面积:两个四分之一圆面积加一个半圆面积,即 $\frac{1}{4}\pi b^2 × 2 + \frac{1}{2}\pi b^2 = \pi b^2$。
窗户面积:$4b × a = 4ab$,能射进阳光的面积:$4ab - \pi b^2$。
(2) $\pi b^2$ 是单项式,次数是 2;$4ab - \pi b^2$ 是多项式,次数是 2。
8. 下列说法正确的是 (
A.$-mn$的系数是1
B.$-2^{2}x^{2}y^{2}$是五次单项式
C.$ab+a-6$的常数项是-6
D.$3x^{2}y^{2}+2xy+x^{2}$是三次多项式
C
)A.$-mn$的系数是1
B.$-2^{2}x^{2}y^{2}$是五次单项式
C.$ab+a-6$的常数项是-6
D.$3x^{2}y^{2}+2xy+x^{2}$是三次多项式
答案:C
解析:
A. $-mn$的系数是$-1$,故A错误;
B. $-2^{2}x^{2}y^{2}$的次数是$2+2=4$,是四次单项式,故B错误;
C. $ab+a-6$的常数项是$-6$,故C正确;
D. $3x^{2}y^{2}+2xy+x^{2}$中最高次项是$3x^{2}y^{2}$,次数为$2+2=4$,是四次多项式,故D错误。
答案:C
B. $-2^{2}x^{2}y^{2}$的次数是$2+2=4$,是四次单项式,故B错误;
C. $ab+a-6$的常数项是$-6$,故C正确;
D. $3x^{2}y^{2}+2xy+x^{2}$中最高次项是$3x^{2}y^{2}$,次数为$2+2=4$,是四次多项式,故D错误。
答案:C