9. 有下列各式:$-\frac {3}{4}x^{2},2x-y,\frac {1}{2025x},\frac {1}{a},x^{2}y+1,-2,\frac {1}{π}$.其中,整式有 (
A.7个
B.6个
C.5个
D.4个
C
)A.7个
B.6个
C.5个
D.4个
答案:C
解析:
解:整式是单项式和多项式的统称,单项式是数或字母的乘积,单独的一个数或一个字母也是单项式;多项式是几个单项式的和。分母中含有字母的式子不是整式。
在给出的各式中:
$-\frac{3}{4}x^{2}$是单项式,属于整式;
$2x - y$是多项式,属于整式;
$\frac{1}{2025x}$分母含有字母,不是整式;
$\frac{1}{a}$分母含有字母,不是整式;
$x^{2}y + 1$是多项式,属于整式;
$-2$是单项式,属于整式;
$\frac{1}{\pi}$,$\pi$是常数,所以是单项式,属于整式。
综上,整式有$-\frac{3}{4}x^{2},2x - y,x^{2}y + 1,-2,\frac{1}{\pi}$,共5个。
答案:C
在给出的各式中:
$-\frac{3}{4}x^{2}$是单项式,属于整式;
$2x - y$是多项式,属于整式;
$\frac{1}{2025x}$分母含有字母,不是整式;
$\frac{1}{a}$分母含有字母,不是整式;
$x^{2}y + 1$是多项式,属于整式;
$-2$是单项式,属于整式;
$\frac{1}{\pi}$,$\pi$是常数,所以是单项式,属于整式。
综上,整式有$-\frac{3}{4}x^{2},2x - y,x^{2}y + 1,-2,\frac{1}{\pi}$,共5个。
答案:C
10. 多项式$\frac {3a^{2}-1}{2}$的常数项为
$-\frac{1}{2}$
.答案:$-\frac{1}{2}$
解析:
解:多项式$\frac{3a^{2} - 1}{2} = \frac{3}{2}a^{2} - \frac{1}{2}$,常数项为$-\frac{1}{2}$。
$-\frac{1}{2}$
$-\frac{1}{2}$
11. (易错题)若多项式$\frac {1}{2}x^{|m|}-(m+2)x+7$是关于x的二次三项式,则$m=$
2
.答案:2 [易错分析]对多项式相关概念理解不清致错。
解析:
解:因为多项式$\frac{1}{2}x^{|m|}-(m+2)x+7$是关于$x$的二次三项式,
所以$|m|=2$且$-(m + 2) \neq 0$。
由$|m|=2$,得$m = \pm 2$。
由$-(m + 2) \neq 0$,得$m \neq -2$。
综上,$m = 2$。
2
所以$|m|=2$且$-(m + 2) \neq 0$。
由$|m|=2$,得$m = \pm 2$。
由$-(m + 2) \neq 0$,得$m \neq -2$。
综上,$m = 2$。
2
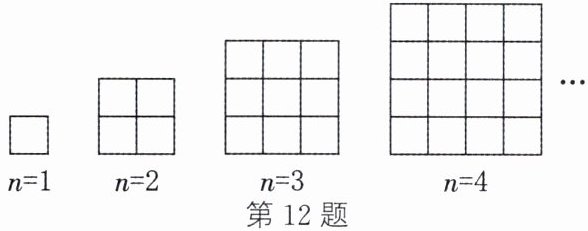
12. 如图所示为由边长为1的小正方形组成的图形,其中第1个图形有$1×1$个小正方形,所有长度为1的线段的长之和为4,第2个图形有$2×2$个小正方形,所有长度为1的线段的长之和为12,第3个图形有$3×3$个小正方形,所有长度为1的线段的长之和为24……按此规律,则第n个图形中所有长度为1的线段的长之和为
$2n(n + 1)$
(用含有n的整式表示).
答案:$2n(n + 1)$ 解析:第 1 个图形有 $1×1$ 个小正方形,所有长度为 1 的线段的长之和为 $4 = 2×1×2$,第 2 个图形有 $2×2$ 个小正方形,所有长度为 1 的线段的长之和为 $12 = 2×2×3$,第 3 个图形有 $3×3$ 个小正方形,所有长度为 1 的线段的长之和为 $24 = 2×3×4$……按此规律,则第 $n$ 个图形中所有长度为 1 的线段的长之和为 $2n(n + 1)$。
解析:
第1个图形:$4=2×1×2$
第2个图形:$12=2×2×3$
第3个图形:$24=2×3×4$
……
第n个图形中所有长度为1的线段的长之和为$2n(n + 1)$
$2n(n + 1)$
第2个图形:$12=2×2×3$
第3个图形:$24=2×3×4$
……
第n个图形中所有长度为1的线段的长之和为$2n(n + 1)$
$2n(n + 1)$
13. 已知关于x的多项式$(a-b)x^{4}+(b-1)x^{3}-(a-2)x^{2}+ax-4中不含x^{3}项与x^{2}$项,试写出这个多项式,并求出当$x= -2$时,这个多项式的值.
答案:由题意,得 $b - 1 = 0$,$-(a - 2) = 0$,所以 $b = 1$,$a = 2$。所以这个多项式为 $x^{4} + 2x - 4$。当 $x = -2$ 时,$x^{4} + 2x - 4 = (-2)^{4} + 2×(-2) - 4 = 8$
解析:
解:因为多项式不含$x^{3}$项与$x^{2}$项,所以$x^{3}$项与$x^{2}$项的系数为$0$。
即$b - 1 = 0$,解得$b = 1$;$-(a - 2) = 0$,解得$a = 2$。
将$a = 2$,$b = 1$代入多项式,得:
$(2 - 1)x^{4} + (1 - 1)x^{3} - (2 - 2)x^{2} + 2x - 4 = x^{4} + 2x - 4$
当$x = -2$时,
$x^{4} + 2x - 4 = (-2)^{4} + 2×(-2) - 4 = 16 - 4 - 4 = 8$
答:这个多项式为$x^{4} + 2x - 4$,当$x = -2$时,多项式的值为$8$。
即$b - 1 = 0$,解得$b = 1$;$-(a - 2) = 0$,解得$a = 2$。
将$a = 2$,$b = 1$代入多项式,得:
$(2 - 1)x^{4} + (1 - 1)x^{3} - (2 - 2)x^{2} + 2x - 4 = x^{4} + 2x - 4$
当$x = -2$时,
$x^{4} + 2x - 4 = (-2)^{4} + 2×(-2) - 4 = 16 - 4 - 4 = 8$
答:这个多项式为$x^{4} + 2x - 4$,当$x = -2$时,多项式的值为$8$。
14. 某旅游团乘轮船出游,轮船顺流航行4h,逆流航行2h.已知轮船在静水中航行的速度为x km/h,水流的速度为y km/h,则轮船一共航行了多少千米? 当$x= 30,y= 10$时,轮船一共航行了多少千米?
答案:轮船一共航行了 $[4(x + y) + 2(x - y)]$ km。当 $x = 30$,$y = 10$ 时,$4(x + y) + 2(x - y) = 4×(30 + 10) + 2×(30 - 10) = 200$,所以轮船一共航行了 200 km
解析:
解:轮船顺流速度为$(x + y)$km/h,顺流航行路程为$4(x + y)$km;逆流速度为$(x - y)$km/h,逆流航行路程为$2(x - y)$km。
一共航行路程为:$4(x + y) + 2(x - y)$km。
当$x = 30$,$y = 10$时,
$4(x + y) + 2(x - y) = 4×(30 + 10) + 2×(30 - 10)$
$= 4×40 + 2×20$
$= 160 + 40$
$= 200$
答:轮船一共航行了$[4(x + y) + 2(x - y)]$千米;当$x = 30$,$y = 10$时,一共航行了200千米。
一共航行路程为:$4(x + y) + 2(x - y)$km。
当$x = 30$,$y = 10$时,
$4(x + y) + 2(x - y) = 4×(30 + 10) + 2×(30 - 10)$
$= 4×40 + 2×20$
$= 160 + 40$
$= 200$
答:轮船一共航行了$[4(x + y) + 2(x - y)]$千米;当$x = 30$,$y = 10$时,一共航行了200千米。
15. 礼堂有长椅x张,现有若干人在礼堂开会,若每张长椅坐5人,则有1张长椅只坐2人,还空出6张长椅.由所提供的信息将在礼堂开会的人数用含x的式子表示出来,并求出当$x= 70$时的人数.
答案:由题意,得 $5(x - 6 - 1) + 2 = 5(x - 7) + 2$,所以在礼堂开会的人数为 $5(x - 7) + 2$。当 $x = 70$ 时,$5(x - 7) + 2 = 5×(70 - 7) + 2 = 317$,所以人数为 317
解析:
解:由题意,得开会人数为 $5(x - 6 - 1) + 2 = 5(x - 7) + 2$。
当 $x = 70$ 时,$5(x - 7) + 2 = 5×(70 - 7) + 2 = 5×63 + 2 = 315 + 2 = 317$。
答:在礼堂开会的人数用含$x$的式子表示为$5(x - 7) + 2$;当$x = 70$时,人数为$317$。
当 $x = 70$ 时,$5(x - 7) + 2 = 5×(70 - 7) + 2 = 5×63 + 2 = 315 + 2 = 317$。
答:在礼堂开会的人数用含$x$的式子表示为$5(x - 7) + 2$;当$x = 70$时,人数为$317$。