10. 有下列各数:$+8,+\frac{3}{4},-7.5\%,\frac{22}{7},9.\dot{8},-2\frac{1}{5},1,0.275$.其中,整数有$a$个,负数有$b$个,正数有$c$个,则$a - b + c$的值为______
6
.答案:6
解析:
整数有:+8,1,共2个,即$a=2$;
负数有:$-7.5\%$,$-2\frac{1}{5}$,共2个,即$b=2$;
正数有:+8,$+\frac{3}{4}$,$\frac{22}{7}$,$9.\dot{8}$,1,0.275,共6个,即$c=6$;
$a - b + c=2 - 2 + 6=6$。
6
负数有:$-7.5\%$,$-2\frac{1}{5}$,共2个,即$b=2$;
正数有:+8,$+\frac{3}{4}$,$\frac{22}{7}$,$9.\dot{8}$,1,0.275,共6个,即$c=6$;
$a - b + c=2 - 2 + 6=6$。
6
11. 先找规律,再填数:$\frac{1}{1}+\frac{1}{2}-1= \frac{1}{2},\frac{1}{3}+\frac{1}{4}-\frac{1}{2}= \frac{1}{12},\frac{1}{5}+\frac{1}{6}-\frac{1}{3}= \frac{1}{30},\frac{1}{7}+\frac{1}{8}-\frac{1}{4}= \frac{1}{56},...$,则$\frac{1}{2025}+\frac{1}{2026}-$
$\frac{1}{1013}$
$=\frac{1}{2025×2026}$.答案:$\frac{1}{1013}$ 解析:通过观察可知,每个等式左边前面的两个分数的分母为两个连续的正整数,第三个分数为第二个分数的 2 倍,等式右边为等式左边前面两个分数的乘积。由此可知,$\frac{1}{2025}+\frac{1}{2026}-\frac{1}{1013}=\frac{1}{2025×2026}$。
解析:
观察等式规律:
第一个等式:$\frac{1}{1}+\frac{1}{2}-\frac{1}{1}=\frac{1}{2}$(第三个分数分母为$2÷2 = 1$)
第二个等式:$\frac{1}{3}+\frac{1}{4}-\frac{1}{2}=\frac{1}{12}$(第三个分数分母为$4÷2 = 2$)
第三个等式:$\frac{1}{5}+\frac{1}{6}-\frac{1}{3}=\frac{1}{30}$(第三个分数分母为$6÷2 = 3$)
第四个等式:$\frac{1}{7}+\frac{1}{8}-\frac{1}{4}=\frac{1}{56}$(第三个分数分母为$8÷2 = 4$)
规律为:等式左边第三个分数的分母是第二个分数分母的一半。
对于$\frac{1}{2025}+\frac{1}{2026}-$______$=\frac{1}{2025×2026}$,第二个分数分母为$2026$,则第三个分数分母为$2026÷2 = 1013$,即该分数为$\frac{1}{1013}$。
答案:$\frac{1}{1013}$
第一个等式:$\frac{1}{1}+\frac{1}{2}-\frac{1}{1}=\frac{1}{2}$(第三个分数分母为$2÷2 = 1$)
第二个等式:$\frac{1}{3}+\frac{1}{4}-\frac{1}{2}=\frac{1}{12}$(第三个分数分母为$4÷2 = 2$)
第三个等式:$\frac{1}{5}+\frac{1}{6}-\frac{1}{3}=\frac{1}{30}$(第三个分数分母为$6÷2 = 3$)
第四个等式:$\frac{1}{7}+\frac{1}{8}-\frac{1}{4}=\frac{1}{56}$(第三个分数分母为$8÷2 = 4$)
规律为:等式左边第三个分数的分母是第二个分数分母的一半。
对于$\frac{1}{2025}+\frac{1}{2026}-$______$=\frac{1}{2025×2026}$,第二个分数分母为$2026$,则第三个分数分母为$2026÷2 = 1013$,即该分数为$\frac{1}{1013}$。
答案:$\frac{1}{1013}$
12. 在某班举行的“数学晚会”上,A,B,C,D,E 五名同学的手上各拿着一张卡片,卡片上分别写着$2,-\frac{1}{2},0,-3,\frac{1}{6}$.主持人按照卡片上的这些数的特征,将这五名同学分成两组或者三组来表演节目(每组人数不限).如果让你来分,那么你会如何分组呢?
答案:答案不唯一,如按正数、非正数分成两组,分别是 $2,\frac{1}{6}$ 和 $-\frac{1}{2},0,-3$
解析:
按正数、负数和零分成三组,分别是$2,\frac{1}{6}$;$-\frac{1}{2},-3$;$0$。
13. 观察下列各数:$\frac{1}{2},-\frac{2}{3},\frac{1}{4},-\frac{4}{5},\frac{1}{6},-\frac{6}{7},...$.请你找出其中的规律,并解答问题:
(1) 第 9 个数是
(2) 第 2025 个数是多少?
(1) 第 9 个数是
$\frac{1}{10}$
,第 14 个数是$-\frac{14}{15}$
;(2) 第 2025 个数是多少?
$\frac{1}{2026}$
答案:(1) $\frac{1}{10}$ $-\frac{14}{15}$ (2) $\frac{1}{2026}$
解析:
(1) 观察数列可知,奇数项为正,分子为1,分母为项数加1;偶数项为负,分子为项数,分母为项数加1。
第9个数是奇数项,分子为1,分母为9+1=10,所以第9个数是$\frac{1}{10}$;
第14个数是偶数项,分子为14,分母为14+1=15,所以第14个数是$-\frac{14}{15}$。
(2) 第2025个数是奇数项,分子为1,分母为2025+1=2026,所以第2025个数是$\frac{1}{2026}$。
(1) $\frac{1}{10}$,$-\frac{14}{15}$;(2) $\frac{1}{2026}$
第9个数是奇数项,分子为1,分母为9+1=10,所以第9个数是$\frac{1}{10}$;
第14个数是偶数项,分子为14,分母为14+1=15,所以第14个数是$-\frac{14}{15}$。
(2) 第2025个数是奇数项,分子为1,分母为2025+1=2026,所以第2025个数是$\frac{1}{2026}$。
(1) $\frac{1}{10}$,$-\frac{14}{15}$;(2) $\frac{1}{2026}$
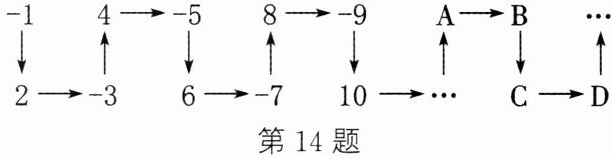
14. 将一串有理数按如图所示的规律排列,解答下列问题:
(1) 在 A 位置上的数是正数还是负数?
(2) A,B,C,D 中哪些位置上的数是负数?
(3) 第 2025 个数是正数还是负数? 对应 A,B,C,D 中的哪个位置?
(1) 在 A 位置上的数是正数还是负数?
(2) A,B,C,D 中哪些位置上的数是负数?
(3) 第 2025 个数是正数还是负数? 对应 A,B,C,D 中的哪个位置?

答案:(1) 在 A 位置上的数是正数 (2) 在 B 和 D 位置上的数是负数 (3) 第 2025 个数是负数 对应 B 位置
解析:
(1) 正数
(2) B,D
(3) 负数,B
(2) B,D
(3) 负数,B