10. 设$(x - 1)^{3} = ax^{3} + bx^{2} + cx + d$,则$a - b + c - d$的值为(
A.2
B.8
C.- 2
D.- 8
B
)A.2
B.8
C.- 2
D.- 8
答案:B
解析:
解:令$x=-1$,代入$(x - 1)^{3} = ax^{3} + bx^{2} + cx + d$,得:
$(-1 - 1)^{3} = a(-1)^{3} + b(-1)^{2} + c(-1) + d$
即$(-2)^{3} = -a + b - c + d$
$-8 = -a + b - c + d$
两边同乘$-1$,得:$a - b + c - d = 8$
答案:B
$(-1 - 1)^{3} = a(-1)^{3} + b(-1)^{2} + c(-1) + d$
即$(-2)^{3} = -a + b - c + d$
$-8 = -a + b - c + d$
两边同乘$-1$,得:$a - b + c - d = 8$
答案:B
11. “m的$\frac{1}{4}$与n的3倍的差”用代数式表示为
$\frac{1}{4}m - 3n$
.答案:$\frac{1}{4}m - 3n$
12. 已知$2a - b + 1$的值为6,则$2 - 3b + 6a$的值为
17
.答案:17
解析:
解:由题意得,$2a - b + 1 = 6$,则$2a - b = 5$。
$2 - 3b + 6a = 6a - 3b + 2 = 3(2a - b) + 2$,
将$2a - b = 5$代入上式,得$3×5 + 2 = 17$。
17
$2 - 3b + 6a = 6a - 3b + 2 = 3(2a - b) + 2$,
将$2a - b = 5$代入上式,得$3×5 + 2 = 17$。
17
13. 某件商品原价b元,先打八五折,再降价10元,则现在的售价是
(0.85b - 10)
元.答案:$(0.85b - 10)$
解析:
解:商品原价为 $ b $ 元,打八五折后的价格为 $ 0.85b $ 元,再降价 10 元后,现在的售价是 $ (0.85b - 10) $ 元。
$ (0.85b - 10) $
$ (0.85b - 10) $
14. 如下表,如果x与y成反比例关系,那么表格中“△”处应填
|x|7|△|
|y|5|14|
2.5
.|x|7|△|
|y|5|14|
答案:2.5
解析:
因为x与y成反比例关系,所以x和y的乘积一定。
当x=7,y=5时,乘积为$7×5 = 35$。
设“△”处的x值为a,则$a×14 = 35$,解得$a = 35÷14 = 2.5$。
2.5
当x=7,y=5时,乘积为$7×5 = 35$。
设“△”处的x值为a,则$a×14 = 35$,解得$a = 35÷14 = 2.5$。
2.5
15. 如图,在一块长为2n、宽为4m的长方形铁皮中,以4m为直径分别剪掉两个半圆. 用含m,n的代数式表示剩下铁皮(涂色部分)的面积为
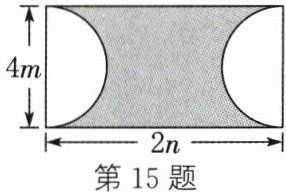
$8mn - 4\pi m^2$
(结果保留π).
答案:$8mn - 4\pi m^2$
解析:
解:长方形铁皮的面积为 $2n × 4m = 8mn$。
两个半圆的直径均为 $4m$,则半径为 $2m$,两个半圆可组成一个整圆,其面积为 $\pi × (2m)^2 = 4\pi m^2$。
剩下铁皮的面积为长方形面积减去圆的面积,即 $8mn - 4\pi m^2$。
故答案为:$8mn - 4\pi m^2$
两个半圆的直径均为 $4m$,则半径为 $2m$,两个半圆可组成一个整圆,其面积为 $\pi × (2m)^2 = 4\pi m^2$。
剩下铁皮的面积为长方形面积减去圆的面积,即 $8mn - 4\pi m^2$。
故答案为:$8mn - 4\pi m^2$
16. 往返于A,B两地的航班,某天由A地到B地时顺风飞行,当天风速为24km/h,飞机顺风飞行需要1.5h到达. 设飞机在无风状态下的速度为xkm/h,用代数式表示A,B两地的距离是
(1.5x + 36)
km.答案:$(1.5x + 36)$
解析:
解:飞机顺风速度为$(x + 24)km/h$,根据路程 = 速度×时间,A,B两地的距离为$1.5(x + 24) = 1.5x + 36$。
$(1.5x + 36)$
$(1.5x + 36)$
17. 如图,数轴上点A所表示的数为$a(a>2)$,现以点P(点P表示的有理数为1)为对折点将数轴向左翻折,则点A的对应点$A'$表示的数为

$2 - a$
(用含a的代数式表示).
答案:$2 - a$
解析:
解:设点$A'$表示的数为$x$。
因为点$P(1)$是点$A$与点$A'$的对折点,所以点$P$到点$A$和点$A'$的距离相等,即$a - 1 = 1 - x$。
解得$x = 2 - a$。
$2 - a$
因为点$P(1)$是点$A$与点$A'$的对折点,所以点$P$到点$A$和点$A'$的距离相等,即$a - 1 = 1 - x$。
解得$x = 2 - a$。
$2 - a$
18. 如图所示为一个数值转换器的原理图. 若开始时输入x的值是1,可发现第1次输出y的值为4,第2次输出y的值为2,第3次输出y的值为1……依次继续下去,则第2025次输出y的值为______.


1
答案:1
解析:
解:由数值转换器原理,输入x=1时:
第1次输出:3×1+1=4
第2次输出:4×1/2=2
第3次输出:2×1/2=1
第4次输出:3×1+1=4
第5次输出:4×1/2=2
第6次输出:2×1/2=1
...
输出结果以4,2,1循环,周期为3。
2025÷3=675,余数为0。
∴第2025次输出y的值为1。
1
第1次输出:3×1+1=4
第2次输出:4×1/2=2
第3次输出:2×1/2=1
第4次输出:3×1+1=4
第5次输出:4×1/2=2
第6次输出:2×1/2=1
...
输出结果以4,2,1循环,周期为3。
2025÷3=675,余数为0。
∴第2025次输出y的值为1。
1
19. (8分)用代数式表示:
(1)比x,y的平方差大3的数;
(2)a的3倍与b的差的平方;
(3)x的平方的倒数减去$\frac{1}{2}$;
(4)x的立方的相反数与2025的和.
(1)比x,y的平方差大3的数;
(2)a的3倍与b的差的平方;
(3)x的平方的倒数减去$\frac{1}{2}$;
(4)x的立方的相反数与2025的和.
答案:(1) $x^2 - y^2 + 3$ (2) $(3a - b)^2$ (3) $\frac{1}{x^2} - \frac{1}{2}$ (4) $-x^3 + 2025$