8. 某市为节约用水,制定了如下标准:每户用水不超过20吨,按每吨1.2元收费;超过20吨,则超出部分按每吨1.5元收费. 如果小明家6月的水费是平均每吨1.25元,那么小明家6月应缴水费(
A.20元
B.24元
C.30元
D.36元
C
)A.20元
B.24元
C.30元
D.36元
答案:C
解析:
解:设小明家6月用水$x$吨。
因为$1.25>1.2$,所以$x>20$。
根据题意,得:
$20×1.2 + 1.5(x - 20) = 1.25x$
$24 + 1.5x - 30 = 1.25x$
$1.5x - 1.25x = 30 - 24$
$0.25x = 6$
$x = 24$
应缴水费:$1.25×24 = 30$(元)
答案:C
因为$1.25>1.2$,所以$x>20$。
根据题意,得:
$20×1.2 + 1.5(x - 20) = 1.25x$
$24 + 1.5x - 30 = 1.25x$
$1.5x - 1.25x = 30 - 24$
$0.25x = 6$
$x = 24$
应缴水费:$1.25×24 = 30$(元)
答案:C
9. 某商店出售了两个进价不同的书包,售价都是42元,其中一个盈利40%,另一个亏损30%,则在这次买卖中,该商店的盈亏情况是(
A.盈利4.2元
B.盈利6元
C.不盈不亏
D.亏损6元
D
)A.盈利4.2元
B.盈利6元
C.不盈不亏
D.亏损6元
答案:D
解析:
解:设盈利40%的书包进价为$x$元,亏损30%的书包进价为$y$元。
对于盈利的书包:$x(1 + 40\%) = 42$,解得$x = 42÷1.4 = 30$(元)。
对于亏损的书包:$y(1 - 30\%) = 42$,解得$y = 42÷0.7 = 60$(元)。
总进价:$30 + 60 = 90$(元),总售价:$42×2 = 84$(元)。
$90 - 84 = 6$(元),所以亏损6元。
答案:D
对于盈利的书包:$x(1 + 40\%) = 42$,解得$x = 42÷1.4 = 30$(元)。
对于亏损的书包:$y(1 - 30\%) = 42$,解得$y = 42÷0.7 = 60$(元)。
总进价:$30 + 60 = 90$(元),总售价:$42×2 = 84$(元)。
$90 - 84 = 6$(元),所以亏损6元。
答案:D
10. 我们知道,无限循环小数都可以转化为分数. 例如:将$0.\dot{6}$转化为分数时,可设$0.\dot{6}= x$,则$x= 0.6+\frac{1}{10}x$,解得$x= \frac{2}{3}$,即$0.\dot{6}= \frac{2}{3}$. 仿照这种方法,将$0.\dot{5}\dot{6}$化成分数是(
A.$\frac{1}{56}$
B.$\frac{7}{8}$
C.$\frac{14}{25}$
D.$\frac{56}{99}$
D
)A.$\frac{1}{56}$
B.$\frac{7}{8}$
C.$\frac{14}{25}$
D.$\frac{56}{99}$
答案:D
解析:
设$0.\dot{5}\dot{6}=x$,则$100x = 56.\dot{5}\dot{6}$,
$100x - x = 56.\dot{5}\dot{6} - 0.\dot{5}\dot{6}$,
$99x = 56$,
解得$x = \frac{56}{99}$。
D
$100x - x = 56.\dot{5}\dot{6} - 0.\dot{5}\dot{6}$,
$99x = 56$,
解得$x = \frac{56}{99}$。
D
11. 已知方程$(m-4)x+2= 2025是关于x$的一元一次方程,则$m$的取值范围是
$ m \neq 4 $
.答案:$ m \neq 4 $
解析:
解:因为方程$(m - 4)x + 2 = 2025$是关于$x$的一元一次方程,所以一次项系数不能为$0$,即$m - 4 \neq 0$,解得$m \neq 4$。
$m \neq 4$
$m \neq 4$
12. 若$\frac{1}{5}a+2= \frac{1}{5}b$,则$a-b-1= $
$-11$
.答案:$-11$
解析:
解:由$\frac{1}{5}a + 2 = \frac{1}{5}b$,等式两边同时乘以5得:$a + 10 = b$,移项可得$a - b = -10$,则$a - b - 1 = -10 - 1 = -11$。
$-11$
$-11$
13. 若$x= m是方程3x-2= 1$的解,则$3m+10$的值为
13
.答案:13
解析:
解:解方程3x-2=1,得x=1。
因为x=m是方程的解,所以m=1。
则3m+10=3×1+10=13。
13
因为x=m是方程的解,所以m=1。
则3m+10=3×1+10=13。
13
远处有一座雄伟的七层宝塔,塔上挂了381盏灯,相邻两层中下一层灯的盏数是上一层灯的盏数的2倍,则塔顶有
3
盏灯.答案:3
解析:
解:设塔顶有$x$盏灯。
由题意得,从顶层依次向下每层灯数为$x$,$2x$,$4x$,$8x$,$16x$,$32x$,$64x$。
$x + 2x + 4x + 8x + 16x + 32x + 64x = 381$
$(1 + 2 + 4 + 8 + 16 + 32 + 64)x = 381$
$127x = 381$
$x = 3$
答:塔顶有$3$盏灯。
由题意得,从顶层依次向下每层灯数为$x$,$2x$,$4x$,$8x$,$16x$,$32x$,$64x$。
$x + 2x + 4x + 8x + 16x + 32x + 64x = 381$
$(1 + 2 + 4 + 8 + 16 + 32 + 64)x = 381$
$127x = 381$
$x = 3$
答:塔顶有$3$盏灯。
15. 服装店销售某款服装,每件服装的标价为400元. 若按标价的八折销售,仍可获利100元,则这款服装每件的标价比进价多
180
元.答案:180
解析:
解:设这款服装每件的进价为$x$元。
按标价的八折销售,售价为$400×0.8 = 320$元。
由题意得:$320 - x = 100$
解得:$x = 320 - 100 = 220$
标价比进价多:$400 - 220 = 180$元。
180
按标价的八折销售,售价为$400×0.8 = 320$元。
由题意得:$320 - x = 100$
解得:$x = 320 - 100 = 220$
标价比进价多:$400 - 220 = 180$元。
180
16. 如果一个长方形内部能用一些正方形铺满,既不重叠,又无缝隙,那么就称它为“优美长方形”. 如图,“优美长方形”ABCD的周长为26,则正方形d的边长为______.
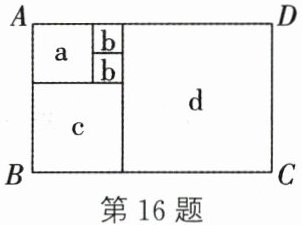

5
答案:5 解析:设正方形 b 的边长为 $ x $,则正方形 a 的边长为 $ 2x $,正方形 c 的边长为 $ 3x $,正方形 d 的边长为 $ 5x $。依题意,得 $ (3x + 5x + 5x) × 2 = 26 $,解得 $ x = 1 $。所以 $ 5x = 5 × 1 = 5 $,即正方形 d 的边长为 5。
解析:
设正方形 b 的边长为 $ x $,则正方形 a 的边长为 $ 2x $,正方形 c 的边长为 $ 3x $,正方形 d 的边长为 $ 5x $。
依题意,长方形周长为 26,可得:
$(3x + 5x + 5x) × 2 = 26$
化简得:$13x × 2 = 26$
即:$26x = 26$
解得:$x = 1$
则正方形 d 的边长为 $ 5x = 5 × 1 = 5 $。
答案:5
依题意,长方形周长为 26,可得:
$(3x + 5x + 5x) × 2 = 26$
化简得:$13x × 2 = 26$
即:$26x = 26$
解得:$x = 1$
则正方形 d 的边长为 $ 5x = 5 × 1 = 5 $。
答案:5
17. 已知方程$\frac{1}{2025}x+2025= 3x-m的解是x= 2024$,则方程$\frac{1}{2025}x+2028= 3x-m+\frac{1}{2025}$的解是______
$x = 2025$
.答案:$ x = 2025 $ 解析:方程 $ \frac{1}{2025}x + 2028 = 3x - m + \frac{1}{2025} $可变形为 $ \frac{1}{2025}(x - 1) + 2025 = 3(x - 1) - m $。因为方程 $ \frac{1}{2025}x + 2025 = 3x - m $的解是 $ x = 2024 $,所以方程 $ \frac{1}{2025}(x - 1) + 2025 = 3(x - 1) - m $中的 $ x - 1 = 2024 $,即此方程的解是 $ x = 2024 + 1 = 2025 $。
解析:
解:方程$\frac{1}{2025}x + 2028 = 3x - m + \frac{1}{2025}$可变形为$\frac{1}{2025}(x - 1) + 2025 = 3(x - 1) - m$。
因为方程$\frac{1}{2025}x + 2025 = 3x - m$的解是$x = 2024$,所以$x - 1 = 2024$,解得$x = 2025$。
答案:$x = 2025$
因为方程$\frac{1}{2025}x + 2025 = 3x - m$的解是$x = 2024$,所以$x - 1 = 2024$,解得$x = 2025$。
答案:$x = 2025$
18. 某公司内部通讯码的后四个数字需加密显示(加密显示可以是多位数),已知加密规则为后四个数字$a,b,c,d分别对应加密号a+2b,2b+c,2c+3d,4d$. 例如:通讯码的后四个数字1,2,3,4分别对应加密号5,7,18,16. 当加密号为18,16,27,36时,通讯码的后四个数字为
2,8,0,9
.答案:2,8,0,9 解析:由题意,得 $ a + 2b = 18 $,$ 2b + c = 16 $,$ 2c + 3d = 27 $,$ 4d = 36 $,解得 $ a = 2 $,$ b = 8 $,$ c = 0 $,$ d = 9 $,即当加密号为 18,16,27,36 时,通讯码的后四个数字为 2,8,0,9。
解析:
解:由题意,得
$4d = 36$,解得$d = 9$;
$2c + 3d = 27$,将$d = 9$代入,得$2c + 3×9 = 27$,$2c = 0$,解得$c = 0$;
$2b + c = 16$,将$c = 0$代入,得$2b = 16$,解得$b = 8$;
$a + 2b = 18$,将$b = 8$代入,得$a + 16 = 18$,解得$a = 2$。
通讯码的后四个数字为2,8,0,9。
$4d = 36$,解得$d = 9$;
$2c + 3d = 27$,将$d = 9$代入,得$2c + 3×9 = 27$,$2c = 0$,解得$c = 0$;
$2b + c = 16$,将$c = 0$代入,得$2b = 16$,解得$b = 8$;
$a + 2b = 18$,将$b = 8$代入,得$a + 16 = 18$,解得$a = 2$。
通讯码的后四个数字为2,8,0,9。