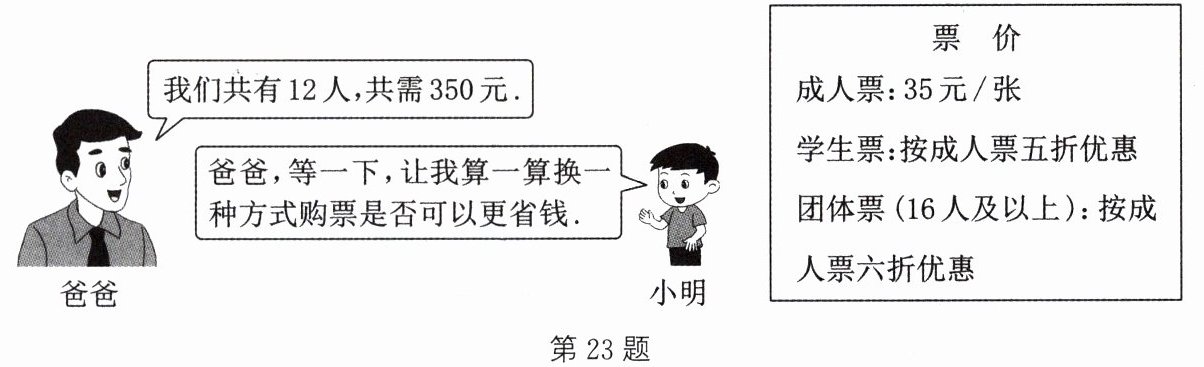
23. (8分)“五一”期间,小明等学生随家长一起到某公园游玩. 购买门票时,小明与爸爸的对话如图所示. 请根据图中的信息,解答下面的问题:
(1)一共去了多少名成人、多少名学生?
(2)请你帮小明算一算,用哪种方式购票更省钱?
(1)一共去了多少名成人、多少名学生?
(2)请你帮小明算一算,用哪种方式购票更省钱?

答案:(1) 设一共去了 $ x $名成人,则去了 $ (12 - x) $名学生。由题意,得 $ 35x + 35 × 0.5(12 - x) = 350 $,解得 $ x = 8 $,则 $ 12 - x = 4 $。所以一共去了 8 名成人、4 名学生 (2) 如果购买团体票,按 16 人计算,那么共需费用为 $ 35 × 0.6 × 16 = 336 $(元)。因为 $ 336 < 350 $,所以购买团体票更省钱
24. (10分)如图①,在数轴上点A表示的数是$-2$,点B在点A的右侧,且到点A的距离是12;点C在点A与点B之间,且点C到点A的距离为4.
(1)点B表示的数是______
(2)如图②,若点P从点A出发,沿数轴以每秒2个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒1个单位长度的速度向左匀速运动. 设运动时间为$t$秒,当点P与点Q相距3个单位长度时,求运动的时间.
(3)在(2)的条件下,若点P与点C之间的距离表示为$PC$,点Q与点B之间的距离表示为$QB$,在运动过程中,是否存在某一时刻使得$PC+QB= 3$?若存在,请求出此时点P表示的数;若不存在,请说明理由.
(1)点B表示的数是______
10
;点C表示的数是______2
.(2)如图②,若点P从点A出发,沿数轴以每秒2个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒1个单位长度的速度向左匀速运动. 设运动时间为$t$秒,当点P与点Q相距3个单位长度时,求运动的时间.
若点 $ P $与点 $ Q $相遇前相距 3 个单位长度,则 $ 2t + t + 3 = 12 $,解得 $ t = 3 $;若点 $ P $与点 $ Q $相遇后相距 3 个单位长度,则 $ 2t + t - 3 = 12 $,解得 $ t = 5 $。综上所述,运动的时间为 3 秒或 5 秒
(3)在(2)的条件下,若点P与点C之间的距离表示为$PC$,点Q与点B之间的距离表示为$QB$,在运动过程中,是否存在某一时刻使得$PC+QB= 3$?若存在,请求出此时点P表示的数;若不存在,请说明理由.
存在 若点 $ P $在点 $ C $的左侧,则 $ PC = 4 - 2t $,$ QB = t $。因为 $ PC + QB = 3 $,所以 $ 4 - 2t + t = 3 $,解得 $ t = 1 $。所以 $ AP = 2t = 2 × 1 = 2 $。因为 $ -2 + 2 = 0 $,所以点 $ P $表示的数为 0。若点 $ P $在点 $ C $的右侧,则 $ PC = 2t - 4 $,$ QB = t $。因为 $ PC + QB = 3 $,所以 $ 2t - 4 + t = 3 $,解得 $ t = \frac{7}{3} $。所以 $ AP = 2t = 2 × \frac{7}{3} = \frac{14}{3} $。因为 $ -2 + \frac{14}{3} = \frac{8}{3} $,所以点 $ P $表示的数为 $ \frac{8}{3} $。综上所述,当 $ t = 1 $或 $ t = \frac{7}{3} $时,$ PC + QB = 3 $,点 $ P $表示的数为 0 或 $ \frac{8}{3} $
答案:(1) 10 2 (2) 若点 $ P $与点 $ Q $相遇前相距 3 个单位长度,则 $ 2t + t + 3 = 12 $,解得 $ t = 3 $;若点 $ P $与点 $ Q $相遇后相距 3 个单位长度,则 $ 2t + t - 3 = 12 $,解得 $ t = 5 $。综上所述,运动的时间为 3 秒或 5 秒 (3) 存在 若点 $ P $在点 $ C $的左侧,则 $ PC = 4 - 2t $,$ QB = t $。因为 $ PC + QB = 3 $,所以 $ 4 - 2t + t = 3 $,解得 $ t = 1 $。所以 $ AP = 2t = 2 × 1 = 2 $。因为 $ -2 + 2 = 0 $,所以点 $ P $表示的数为 0。若点 $ P $在点 $ C $的右侧,则 $ PC = 2t - 4 $,$ QB = t $。因为 $ PC + QB = 3 $,所以 $ 2t - 4 + t = 3 $,解得 $ t = \frac{7}{3} $。所以 $ AP = 2t = 2 × \frac{7}{3} = \frac{14}{3} $。因为 $ -2 + \frac{14}{3} = \frac{8}{3} $,所以点 $ P $表示的数为 $ \frac{8}{3} $。综上所述,当 $ t = 1 $或 $ t = \frac{7}{3} $时,$ PC + QB = 3 $,点 $ P $表示的数为 0 或 $ \frac{8}{3} $
解析:
(1) 10;2
(2) 解:点A表示的数是-2,点B表示的数是10,所以AB=12。
点P从点A出发,速度为每秒2个单位长度,运动t秒后,点P表示的数为-2+2t;点Q从点B出发,速度为每秒1个单位长度,运动t秒后,点Q表示的数为10-t。
当点P与点Q相遇前相距3个单位长度时,可得方程:(10-t)-(-2+2t)=3,即10-t+2-2t=3,12-3t=3,3t=9,解得t=3。
当点P与点Q相遇后相距3个单位长度时,可得方程:(-2+2t)-(10-t)=3,即-2+2t-10+t=3,3t-12=3,3t=15,解得t=5。
综上所述,运动的时间为3秒或5秒。
(3) 解:点C表示的数是2,点P表示的数为-2+2t,所以PC=|(-2+2t)-2|=|2t-4|;点Q表示的数为10-t,所以QB=|10-(10-t)|=t(因为点Q向左运动,t≥0,所以QB=t)。
因为PC+QB=3,所以|2t-4|+t=3。
当2t-4≥0,即t≥2时,方程为2t-4+t=3,3t=7,解得t=7/3。此时点P表示的数为-2+2×(7/3)=-2+14/3=8/3。
当2t-4<0,即t<2时,方程为4-2t+t=3,4-t=3,解得t=1。此时点P表示的数为-2+2×1=0。
综上所述,存在某一时刻使得PC+QB=3,此时点P表示的数为0或8/3。
(2) 解:点A表示的数是-2,点B表示的数是10,所以AB=12。
点P从点A出发,速度为每秒2个单位长度,运动t秒后,点P表示的数为-2+2t;点Q从点B出发,速度为每秒1个单位长度,运动t秒后,点Q表示的数为10-t。
当点P与点Q相遇前相距3个单位长度时,可得方程:(10-t)-(-2+2t)=3,即10-t+2-2t=3,12-3t=3,3t=9,解得t=3。
当点P与点Q相遇后相距3个单位长度时,可得方程:(-2+2t)-(10-t)=3,即-2+2t-10+t=3,3t-12=3,3t=15,解得t=5。
综上所述,运动的时间为3秒或5秒。
(3) 解:点C表示的数是2,点P表示的数为-2+2t,所以PC=|(-2+2t)-2|=|2t-4|;点Q表示的数为10-t,所以QB=|10-(10-t)|=t(因为点Q向左运动,t≥0,所以QB=t)。
因为PC+QB=3,所以|2t-4|+t=3。
当2t-4≥0,即t≥2时,方程为2t-4+t=3,3t=7,解得t=7/3。此时点P表示的数为-2+2×(7/3)=-2+14/3=8/3。
当2t-4<0,即t<2时,方程为4-2t+t=3,4-t=3,解得t=1。此时点P表示的数为-2+2×1=0。
综上所述,存在某一时刻使得PC+QB=3,此时点P表示的数为0或8/3。