1. 从上面看如图所示的立体图形,得到的平面图形是(
C
)答案:C
2. 下列图形是棱锥侧面展开图的为(
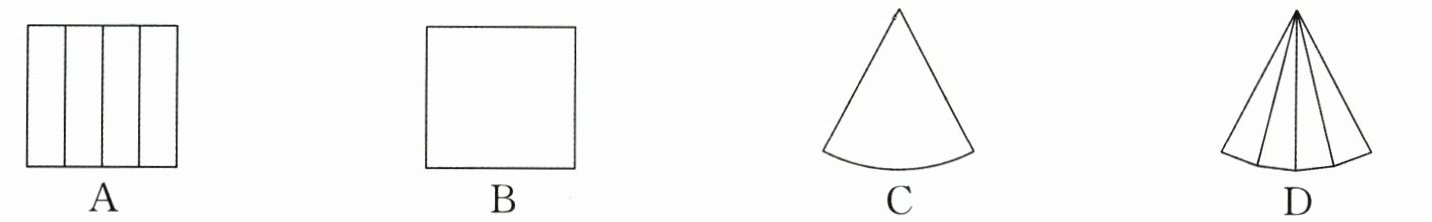
D
)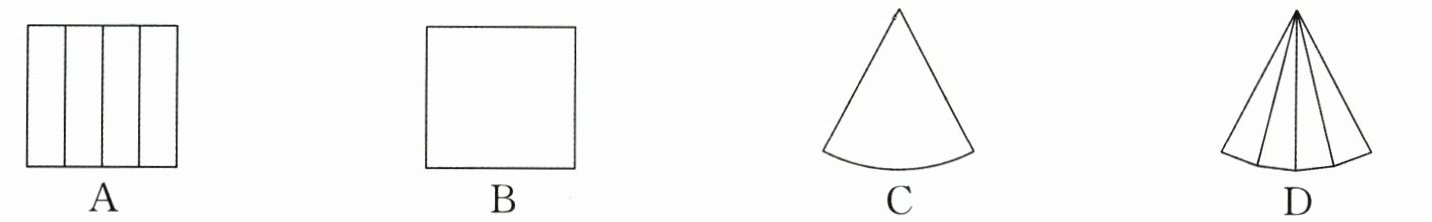
答案:D
3. 上午9:20时,时钟的时针与分针所夹角的度数是(
A.$150^{\circ}$
B.$160^{\circ}$
C.$162^{\circ}$
D.$165^{\circ}$
B
)A.$150^{\circ}$
B.$160^{\circ}$
C.$162^{\circ}$
D.$165^{\circ}$
答案:B
解析:
解:时针每分钟转$0.5^{\circ}$,分针每分钟转$6^{\circ}$。
9时整,时针与分针夹角为$9×30^{\circ}=270^{\circ}$。
20分钟内,时针转$20×0.5^{\circ}=10^{\circ}$,分针转$20×6^{\circ}=120^{\circ}$。
9:20时,夹角为$270^{\circ}+10^{\circ}-120^{\circ}=160^{\circ}$。
答案:B
9时整,时针与分针夹角为$9×30^{\circ}=270^{\circ}$。
20分钟内,时针转$20×0.5^{\circ}=10^{\circ}$,分针转$20×6^{\circ}=120^{\circ}$。
9:20时,夹角为$270^{\circ}+10^{\circ}-120^{\circ}=160^{\circ}$。
答案:B
4. 根据下列线段的长度,能判断A,B,C三点不在同一条直线上的是(
A.$AB = 8cm$,$BC = 19cm$,$AC = 27cm$
B.$AB = 10cm$,$BC = 9cm$,$AC = 18.9cm$
C.$AB = 21cm$,$BC = 11cm$,$AC = 10cm$
D.$AB = 7.5cm$,$BC = 14cm$,$AC = 6.5cm$
B
)A.$AB = 8cm$,$BC = 19cm$,$AC = 27cm$
B.$AB = 10cm$,$BC = 9cm$,$AC = 18.9cm$
C.$AB = 21cm$,$BC = 11cm$,$AC = 10cm$
D.$AB = 7.5cm$,$BC = 14cm$,$AC = 6.5cm$
答案:B
解析:
解:
A. $AB + AC = 8 + 27 = 35$,$BC = 19$,$35 \neq 19$;$AB + BC = 8 + 19 = 27 = AC$,三点共线。
B. $AB + BC = 10 + 9 = 19$,$AC = 18.9$,$19 \neq 18.9$;$AB + AC = 10 + 18.9 = 28.9$,$BC = 9$,$28.9 \neq 9$;$BC + AC = 9 + 18.9 = 27.9$,$AB = 10$,$27.9 \neq 10$,三点不共线。
C. $BC + AC = 11 + 10 = 21 = AB$,三点共线。
D. $AB + AC = 7.5 + 6.5 = 14 = BC$,三点共线。
结论:B
A. $AB + AC = 8 + 27 = 35$,$BC = 19$,$35 \neq 19$;$AB + BC = 8 + 19 = 27 = AC$,三点共线。
B. $AB + BC = 10 + 9 = 19$,$AC = 18.9$,$19 \neq 18.9$;$AB + AC = 10 + 18.9 = 28.9$,$BC = 9$,$28.9 \neq 9$;$BC + AC = 9 + 18.9 = 27.9$,$AB = 10$,$27.9 \neq 10$,三点不共线。
C. $BC + AC = 11 + 10 = 21 = AB$,三点共线。
D. $AB + AC = 7.5 + 6.5 = 14 = BC$,三点共线。
结论:B
5. 如图,下列表示不正确的是(
A.$AB + BC = AC$
B.$\angle C = \angle \alpha$
C.$\angle B + \angle ABD = 180^{\circ}$
D.$\angle 1 + \angle 2 = \angle ADC$
C
)A.$AB + BC = AC$
B.$\angle C = \angle \alpha$
C.$\angle B + \angle ABD = 180^{\circ}$
D.$\angle 1 + \angle 2 = \angle ADC$
答案:C
解析:
解:A. 由图可知,点B在AC上,所以AB + BC = AC,正确;
B. 由图可知,∠C与∠α表示同一个角,所以∠C = ∠α,正确;
C. 由图可知,∠B与∠ABD是同一个角,所以∠B + ∠ABD = 2∠B,不一定等于180°,错误;
D. 由图可知,∠ADC是∠1与∠2的和,所以∠1 + ∠2 = ∠ADC,正确。
故选C。
B. 由图可知,∠C与∠α表示同一个角,所以∠C = ∠α,正确;
C. 由图可知,∠B与∠ABD是同一个角,所以∠B + ∠ABD = 2∠B,不一定等于180°,错误;
D. 由图可知,∠ADC是∠1与∠2的和,所以∠1 + ∠2 = ∠ADC,正确。
故选C。
6. 已知线段$AB = 8$,延长线段$AB至点C$,使得$BC = \frac{1}{2}AB$,延长线段$BA至点D$,使得$AD = \frac{1}{4}AB$,则$CD$的长为(
A.10
B.12
C.14
D.16
C
)A.10
B.12
C.14
D.16
答案:C
解析:
解:
∵ $ AB = 8 $,
∴ $ BC = \frac{1}{2}AB = \frac{1}{2} × 8 = 4 $,
$ AD = \frac{1}{4}AB = \frac{1}{4} × 8 = 2 $。
由题意知,点D、A、B、C在同一直线上,且D在BA延长线上,C在AB延长线上,
∴ $ CD = AD + AB + BC = 2 + 8 + 4 = 14 $。
答案:C
∵ $ AB = 8 $,
∴ $ BC = \frac{1}{2}AB = \frac{1}{2} × 8 = 4 $,
$ AD = \frac{1}{4}AB = \frac{1}{4} × 8 = 2 $。
由题意知,点D、A、B、C在同一直线上,且D在BA延长线上,C在AB延长线上,
∴ $ CD = AD + AB + BC = 2 + 8 + 4 = 14 $。
答案:C
7. 有下列说法:①若$\angle \alpha = 35^{\circ}$,则$\angle \alpha的余角的度数是55^{\circ}$;②若$\angle \alpha = 32^{\circ}13'46''$,则$\angle \alpha的补角的度数是147^{\circ}46'14''$;③$6.75^{\circ}$用度、分、秒来表示为$6^{\circ}45'$;④$36^{\circ}48'36''用度来表示为36.81^{\circ}$。其中,正确的有(
A.①②③④
B.①②③
C.②③④
D.①③④
A
)A.①②③④
B.①②③
C.②③④
D.①③④
答案:A
解析:
解:①$90^{\circ}-35^{\circ}=55^{\circ}$,正确;
②$180^{\circ}-32^{\circ}13'46''=147^{\circ}46'14''$,正确;
③$0.75^{\circ}=0.75×60'=45'$,$6.75^{\circ}=6^{\circ}45'$,正确;
④$36''=36÷60'=0.6'$,$48.6'=48.6÷60^{\circ}=0.81^{\circ}$,$36^{\circ}48'36''=36.81^{\circ}$,正确。
结论:①②③④均正确。
答案:A
②$180^{\circ}-32^{\circ}13'46''=147^{\circ}46'14''$,正确;
③$0.75^{\circ}=0.75×60'=45'$,$6.75^{\circ}=6^{\circ}45'$,正确;
④$36''=36÷60'=0.6'$,$48.6'=48.6÷60^{\circ}=0.81^{\circ}$,$36^{\circ}48'36''=36.81^{\circ}$,正确。
结论:①②③④均正确。
答案:A
8. 如图,线段$AB$表示一根对折以后的绳子,现从点$P$处把绳子剪断,剪断后的各段绳子中最长的一段为$8cm$。若$AP = \frac{1}{2}PB$,则这根绳子的原长为(
A.$12cm$
B.$24cm$
C.$20cm或24cm$
D.$12cm或24cm$
D
)A.$12cm$
B.$24cm$
C.$20cm或24cm$
D.$12cm或24cm$
答案:D
解析:
设 $ PB = x \, \text{cm} $,则 $ AP = \frac{1}{2}x \, \text{cm} $,$ AB = AP + PB = \frac{3}{2}x \, \text{cm} $,绳子原长为 $ 2AB = 3x \, \text{cm} $。
情况1:点P靠近A点
剪断后最长段为对折后含B点的部分,即 $ 2PB = 8 \, \text{cm} $。
$ 2x = 8 \implies x = 4 $。
原长 $ 3x = 3 × 4 = 12 \, \text{cm} $。
情况2:点P靠近B点
剪断后最长段为对折后含A点的部分,即 $ 2AP = 8 \, \text{cm} $。
$ 2 × \frac{1}{2}x = 8 \implies x = 8 $。
原长 $ 3x = 3 × 8 = 24 \, \text{cm} $。
综上,绳子原长为 $ 12 \, \text{cm} $ 或 $ 24 \, \text{cm} $。
答案:D
情况1:点P靠近A点
剪断后最长段为对折后含B点的部分,即 $ 2PB = 8 \, \text{cm} $。
$ 2x = 8 \implies x = 4 $。
原长 $ 3x = 3 × 4 = 12 \, \text{cm} $。
情况2:点P靠近B点
剪断后最长段为对折后含A点的部分,即 $ 2AP = 8 \, \text{cm} $。
$ 2 × \frac{1}{2}x = 8 \implies x = 8 $。
原长 $ 3x = 3 × 8 = 24 \, \text{cm} $。
综上,绳子原长为 $ 12 \, \text{cm} $ 或 $ 24 \, \text{cm} $。
答案:D