23. (8分)如图,数轴上有两条线段$AB$,$CD$,线段$AB$的长为3个单位长度,线段$CD$的长为4个单位长度,线段的端点$A$,$B$,$C$,$D在数轴上分别与数-4$,$-1$,$2$,$6$对应。将线段$AB$,$CD$分别以每秒2个单位长度、每秒1个单位长度的速度沿数轴同时向右移动,设移动时间为$ts$。
(1)当$t = 2$时,点$A$表示的数是
(2)移动过程中,若线段$AB$,$CD$重叠部分的长为1个单位长度,求$t$的值。
(3)$M$,$N$是数轴上的两个动点,设$M是线段AC$的中点,$N是线段BD$的中点。移动过程中,若$DM = 2AN$,直接写出$t$的值。
(1)当$t = 2$时,点$A$表示的数是
0
,点$D$表示的数是8
。(2)移动过程中,若线段$AB$,$CD$重叠部分的长为1个单位长度,求$t$的值。
当运动时间为 $ t \mathrm{s} $ 时,点 $ A $ 表示的数为 $ -4 + 2t $,点 $ B $ 表示的数为 $ -1 + 2t $,点 $ C $ 表示的数为 $ 2 + t $,点 $ D $ 表示的数为 $ 6 + t $。当点 $ B $ 在点 $ C $ 右侧且 $ BC = 1 $ 时,$ -1 + 2t - (2 + t) = 1 $,解得 $ t = 4 $;当点 $ D $ 在点 $ A $ 右侧且 $ AD = 1 $ 时,$ 6 + t - (-4 + 2t) = 1 $,解得 $ t = 9 $。所以 $ t $ 的值为 $ 4 $ 或 $ 9 $
(3)$M$,$N$是数轴上的两个动点,设$M是线段AC$的中点,$N是线段BD$的中点。移动过程中,若$DM = 2AN$,直接写出$t$的值。
由 (2) 知,当运动时间为 $ t \mathrm{s} $ 时,点 $ A $ 表示的数为 $ -4 + 2t $,点 $ B $ 表示的数为 $ -1 + 2t $,点 $ C $ 表示的数为 $ 2 + t $,点 $ D $ 表示的数为 $ 6 + t $。因为 $ M $ 是线段 $ AC $ 的中点,$ N $ 是线段 $ BD $ 的中点,所以点 $ M $ 表示的数为 $ \frac{-4 + 2t + 2 + t}{2} = -1 + \frac{3}{2}t $,点 $ N $ 表示的数为 $ \frac{-1 + 2t + 6 + t}{2} = \frac{5}{2} + \frac{3}{2}t $。根据题意,得 $ \left|6 + t - \left(-1 + \frac{3}{2}t\right)\right| = 2\left|-4 + 2t - \left(\frac{5}{2} + \frac{3}{2}t\right)\right| $,即 $ 7 - \frac{1}{2}t = 2\left(\frac{13}{2} - \frac{1}{2}t\right) $ 或 $ 7 - \frac{1}{2}t = 2\left(\frac{1}{2}t - \frac{13}{2}\right) $,解得 $ t = 12 $ 或 $ t = \frac{40}{3} $。所以 $ t $ 的值为 $ 12 $ 或 $ \frac{40}{3} $
答案:(1) $ 0 $ $ 8 $ (2) 当运动时间为 $ t \mathrm{s} $ 时,点 $ A $ 表示的数为 $ -4 + 2t $,点 $ B $ 表示的数为 $ -1 + 2t $,点 $ C $ 表示的数为 $ 2 + t $,点 $ D $ 表示的数为 $ 6 + t $。当点 $ B $ 在点 $ C $ 右侧且 $ BC = 1 $ 时,$ -1 + 2t - (2 + t) = 1 $,解得 $ t = 4 $;当点 $ D $ 在点 $ A $ 右侧且 $ AD = 1 $ 时,$ 6 + t - (-4 + 2t) = 1 $,解得 $ t = 9 $。所以 $ t $ 的值为 $ 4 $ 或 $ 9 $ (3) 由 (2) 知,当运动时间为 $ t \mathrm{s} $ 时,点 $ A $ 表示的数为 $ -4 + 2t $,点 $ B $ 表示的数为 $ -1 + 2t $,点 $ C $ 表示的数为 $ 2 + t $,点 $ D $ 表示的数为 $ 6 + t $。因为 $ M $ 是线段 $ AC $ 的中点,$ N $ 是线段 $ BD $ 的中点,所以点 $ M $ 表示的数为 $ \frac{-4 + 2t + 2 + t}{2} = -1 + \frac{3}{2}t $,点 $ N $ 表示的数为 $ \frac{-1 + 2t + 6 + t}{2} = \frac{5}{2} + \frac{3}{2}t $。根据题意,得 $ \left|6 + t - \left(-1 + \frac{3}{2}t\right)\right| = 2\left|-4 + 2t - \left(\frac{5}{2} + \frac{3}{2}t\right)\right| $,即 $ 7 - \frac{1}{2}t = 2\left(\frac{13}{2} - \frac{1}{2}t\right) $ 或 $ 7 - \frac{1}{2}t = 2\left(\frac{1}{2}t - \frac{13}{2}\right) $,解得 $ t = 12 $ 或 $ t = \frac{40}{3} $。所以 $ t $ 的值为 $ 12 $ 或 $ \frac{40}{3} $
解析:
(1) 0;8
(2) 解:当运动时间为$t\,\text{s}$时,点$A$表示的数为$-4 + 2t$,点$B$表示的数为$-1 + 2t$,点$C$表示的数为$2 + t$,点$D$表示的数为$6 + t$。
当线段$AB$与$CD$重叠部分长为1个单位长度时,分两种情况:
① 点$B$在点$C$右侧且$BC = 1$,则$-1 + 2t-(2 + t)=1$,解得$t = 4$;
② 点$D$在点$A$右侧且$AD = 1$,则$6 + t-(-4 + 2t)=1$,解得$t = 9$。
综上,$t$的值为$4$或$9$。
(3)$t = 12$或$t=\frac{40}{3}$
(2) 解:当运动时间为$t\,\text{s}$时,点$A$表示的数为$-4 + 2t$,点$B$表示的数为$-1 + 2t$,点$C$表示的数为$2 + t$,点$D$表示的数为$6 + t$。
当线段$AB$与$CD$重叠部分长为1个单位长度时,分两种情况:
① 点$B$在点$C$右侧且$BC = 1$,则$-1 + 2t-(2 + t)=1$,解得$t = 4$;
② 点$D$在点$A$右侧且$AD = 1$,则$6 + t-(-4 + 2t)=1$,解得$t = 9$。
综上,$t$的值为$4$或$9$。
(3)$t = 12$或$t=\frac{40}{3}$
24. (10分)定义:若两个角的和为$60^{\circ}$,则称这两个角互为“幸运角”。已知$\angle AOB = \alpha$($\alpha大于0^{\circ}且小于30^{\circ}$),$\angle AOB与\angle AOC$互为“幸运角”,$\angle AOB与\angle AOD$互补(本题所研究的角均大于$0^{\circ}且小于180^{\circ}$)。
(1)如图,当$OB在\angle AOC$的内部,且点$B$,$D在OA$的同侧时。
① 若$\angle BOC = 10^{\circ}$,则$\alpha =$
② 若射线$OM在\angle AOD$内部,且满足$\angle DOM = 2\angle AOM$,求$\angle COM$的度数(用含$\alpha$的式子表示)。
(2)求出$\angle COD$所有可能的度数(用含$\alpha$的式子表示)。
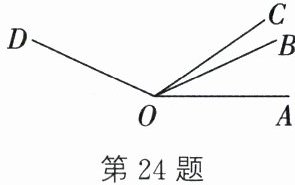
(1)如图,当$OB在\angle AOC$的内部,且点$B$,$D在OA$的同侧时。
① 若$\angle BOC = 10^{\circ}$,则$\alpha =$
$25^{\circ}$
;② 若射线$OM在\angle AOD$内部,且满足$\angle DOM = 2\angle AOM$,求$\angle COM$的度数(用含$\alpha$的式子表示)。
因为 $ \angle AOB $ 与 $ \angle AOD $ 互补,$ \angle AOB = \alpha $,所以 $ \angle AOD = 180^{\circ} - \alpha $。因为 $ \angle AOB $ 与 $ \angle AOC $ 互为“幸运角”,所以 $ \angle AOB + \angle AOC = 60^{\circ} $。所以 $ \angle AOC = 60^{\circ} - \alpha $。因为射线 $ OM $ 在 $ \angle AOD $ 内部,且满足 $ \angle DOM = 2\angle AOM $,所以 $ \angle AOM = \frac{1}{3}\angle AOD = \frac{1}{3}(180^{\circ} - \alpha) = 60^{\circ} - \frac{1}{3}\alpha $。所以 $ \angle AOC < \angle AOM $。所以 $ \angle COM = \angle AOM - \angle AOC = \left(60^{\circ} - \frac{1}{3}\alpha\right) - (60^{\circ} - \alpha) = \frac{2}{3}\alpha $
(2)求出$\angle COD$所有可能的度数(用含$\alpha$的式子表示)。
当 $ OB $ 在 $ \angle AOC $ 的内部,点 $ B $,$ D $ 在 $ OA $ 的同侧时,$ \angle COD = \angle AOD - \angle AOC = (180^{\circ} - \alpha) - (60^{\circ} - \alpha) = 120^{\circ} $;当 $ OB $ 在 $ \angle AOC $ 的内部,点 $ B $,$ D $ 在 $ OA $ 的两侧时,如图 ①,$ \angle COD = 360^{\circ} - (\angle AOC + \angle AOD) = 360^{\circ} - [(60^{\circ} - \alpha) + (180^{\circ} - \alpha)] = 120^{\circ} + 2\alpha $;当 $ OB $ 在 $ \angle AOC $ 的外部,点 $ B $,$ D $ 在 $ OA $ 的同侧时,如图 ②,$ \angle COD = 360^{\circ} - (\angle AOC + \angle AOD) = 360^{\circ} - [(60^{\circ} - \alpha) + (180^{\circ} - \alpha)] = 120^{\circ} + 2\alpha $;当 $ OB $ 在 $ \angle AOC $ 的外部,点 $ B $,$ D $ 在 $ OA $ 的两侧时,如图 ③,$ \angle COD = \angle AOD - \angle AOC = (180^{\circ} - \alpha) - (60^{\circ} - \alpha) = 120^{\circ} $。综上所述,$ \angle COD $ 所有可能的度数是 $ 120^{\circ} $ 或 $ 120^{\circ} + 2\alpha $

答案:(1) ① $ 25^{\circ} $ ② 因为 $ \angle AOB $ 与 $ \angle AOD $ 互补,$ \angle AOB = \alpha $,所以 $ \angle AOD = 180^{\circ} - \alpha $。因为 $ \angle AOB $ 与 $ \angle AOC $ 互为“幸运角”,所以 $ \angle AOB + \angle AOC = 60^{\circ} $。所以 $ \angle AOC = 60^{\circ} - \alpha $。因为射线 $ OM $ 在 $ \angle AOD $ 内部,且满足 $ \angle DOM = 2\angle AOM $,所以 $ \angle AOM = \frac{1}{3}\angle AOD = \frac{1}{3}(180^{\circ} - \alpha) = 60^{\circ} - \frac{1}{3}\alpha $。所以 $ \angle AOC < \angle AOM $。所以 $ \angle COM = \angle AOM - \angle AOC = \left(60^{\circ} - \frac{1}{3}\alpha\right) - (60^{\circ} - \alpha) = \frac{2}{3}\alpha $ (2) 当 $ OB $ 在 $ \angle AOC $ 的内部,点 $ B $,$ D $ 在 $ OA $ 的同侧时,$ \angle COD = \angle AOD - \angle AOC = (180^{\circ} - \alpha) - (60^{\circ} - \alpha) = 120^{\circ} $;当 $ OB $ 在 $ \angle AOC $ 的内部,点 $ B $,$ D $ 在 $ OA $ 的两侧时,如图 ①,$ \angle COD = 360^{\circ} - (\angle AOC + \angle AOD) = 360^{\circ} - [(60^{\circ} - \alpha) + (180^{\circ} - \alpha)] = 120^{\circ} + 2\alpha $;当 $ OB $ 在 $ \angle AOC $ 的外部,点 $ B $,$ D $ 在 $ OA $ 的同侧时,如图 ②,$ \angle COD = 360^{\circ} - (\angle AOC + \angle AOD) = 360^{\circ} - [(60^{\circ} - \alpha) + (180^{\circ} - \alpha)] = 120^{\circ} + 2\alpha $;当 $ OB $ 在 $ \angle AOC $ 的外部,点 $ B $,$ D $ 在 $ OA $ 的两侧时,如图 ③,$ \angle COD = \angle AOD - \angle AOC = (180^{\circ} - \alpha) - (60^{\circ} - \alpha) = 120^{\circ} $。综上所述,$ \angle COD $ 所有可能的度数是 $ 120^{\circ} $ 或 $ 120^{\circ} + 2\alpha $