8. 若代数式$ax - 3$的部分对应值如下表,则关于$x的一元一次方程ax - 3 = 0$的解在如图所示的数轴上的对应点可能是(
| $x$ | …$$ | $-2$ | $0$ | $2$ | …$$ |
| $ax - 3$ | …$$ | $2$ | $-3$ | $-8$ | …$$ |
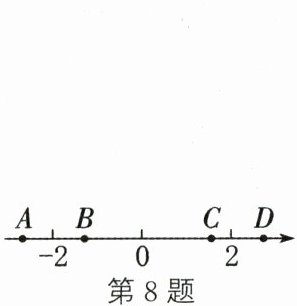
A.$A$
B.$B$
C.$C$
D.$D$
B
)| $x$ | …$$ | $-2$ | $0$ | $2$ | …$$ |
| $ax - 3$ | …$$ | $2$ | $-3$ | $-8$ | …$$ |

A.$A$
B.$B$
C.$C$
D.$D$
答案:B
解析:
解:当$x = -2$时,$ax - 3 = 2$,即$-2a - 3 = 2$,解得$a = -2.5$。
方程$ax - 3 = 0$为$-2.5x - 3 = 0$,解得$x = -1.2$。
在数轴上,$-1.2$对应点为$B$。
答案:B
方程$ax - 3 = 0$为$-2.5x - 3 = 0$,解得$x = -1.2$。
在数轴上,$-1.2$对应点为$B$。
答案:B
9. 如图,把一副三角尺$ABC与BDE$拼在一起,其中$A$,$D$,$B$三点在同一条直线上,$BM为∠ABC$的平分线,$BN为∠CBE$的平分线,则$∠MBN$的度数是(
A.$30^{\circ}$
B.$45^{\circ}$
C.$55^{\circ}$
D.$60^{\circ}$
B
)A.$30^{\circ}$
B.$45^{\circ}$
C.$55^{\circ}$
D.$60^{\circ}$
答案:B
10. 如图,将其中的三个正方形区域记为①②③,区域④是区域②和③的公共部分,余下两个区域的面积分别记为$S_{1}和S_{2}$. 已知区域①②③的边长分别为100米,200米和300米,则下列结论一定正确的是( )

A.$S_{1}= \frac{2}{3}S_{2}$
B.$S_{1}= \frac{1}{2}S_{2}$
C.$S_{1}= S_{2}-100$
D.$S_{1}= S_{2}-200$

A.$S_{1}= \frac{2}{3}S_{2}$
B.$S_{1}= \frac{1}{2}S_{2}$
C.$S_{1}= S_{2}-100$
D.$S_{1}= S_{2}-200$
答案:
解析:如图,由①③可得$GH = 300 + 100 = 400$(米),所以$GF = 400 - 200 = 200$(米)。设$CD = a$米,则$IH = 300 + 200 - a = (500 - a)$米,所以$AB = 500 - a - 200 - 100 = (200 - a)$米,$EF = 500 - a - 300 = (200 - a)$米。由题意,得$AI = 100$米。所以$S_{1} = 100×(200 - a)$平方米,$S_{2} = 200×(200 - a)$平方米,所以$S_{1} = \frac{1}{2}S_{2}$。

解析:如图,由①③可得$GH = 300 + 100 = 400$(米),所以$GF = 400 - 200 = 200$(米)。设$CD = a$米,则$IH = 300 + 200 - a = (500 - a)$米,所以$AB = 500 - a - 200 - 100 = (200 - a)$米,$EF = 500 - a - 300 = (200 - a)$米。由题意,得$AI = 100$米。所以$S_{1} = 100×(200 - a)$平方米,$S_{2} = 200×(200 - a)$平方米,所以$S_{1} = \frac{1}{2}S_{2}$。

11. 比较大小:$5$
>
$-3$(填“$>$”或“$<$”).答案:>
12. 已知$y与x$成反比例关系,当$x = 4$时,$y = 6$,则当$x = 3$时,$y = $
8
.答案:8
解析:
解:设反比例函数的解析式为$y = \frac{k}{x}$($k$为常数,$k \neq 0$)。
因为当$x = 4$时,$y = 6$,所以$6 = \frac{k}{4}$,解得$k = 4×6 = 24$。
则反比例函数的解析式为$y = \frac{24}{x}$。
当$x = 3$时,$y = \frac{24}{3} = 8$。
8
因为当$x = 4$时,$y = 6$,所以$6 = \frac{k}{4}$,解得$k = 4×6 = 24$。
则反比例函数的解析式为$y = \frac{24}{x}$。
当$x = 3$时,$y = \frac{24}{3} = 8$。
8
13. 若$-x^{a}y^{2}与5x^{4}y^{2}$的差是单项式,则常数$a$的值为
4
.答案:4
解析:
解:因为$-x^{a}y^{2}$与$5x^{4}y^{2}$的差是单项式,所以这两个单项式是同类项。
同类项要求相同字母的指数相同,对于$x$的指数,可得$a = 4$。
4
同类项要求相同字母的指数相同,对于$x$的指数,可得$a = 4$。
4
14. 如果$-2a^{2} + 3b - 8$的值为1,那么$4a^{2} - 6b - 8$的值为
−26
.答案:−26
解析:
解:由题意得,$-2a^{2} + 3b - 8 = 1$,则$-2a^{2} + 3b = 9$。
两边同时乘以$-2$,得$4a^{2} - 6b = -18$。
所以$4a^{2} - 6b - 8 = -18 - 8 = -26$。
$-26$
两边同时乘以$-2$,得$4a^{2} - 6b = -18$。
所以$4a^{2} - 6b - 8 = -18 - 8 = -26$。
$-26$
15. 已知关于$x的方程\frac{x}{2}+\frac{m}{3}= x - 4与方程2x + 5 = 3(x - 1)$的解相同,则$m = $
0
.答案:0
解析:
解:解方程$2x + 5 = 3(x - 1)$
$2x + 5 = 3x - 3$
$5 + 3 = 3x - 2x$
$x = 8$
将$x = 8$代入$\frac{x}{2}+\frac{m}{3}= x - 4$
$\frac{8}{2}+\frac{m}{3}= 8 - 4$
$4 + \frac{m}{3}= 4$
$\frac{m}{3}= 0$
$m = 0$
0
$2x + 5 = 3x - 3$
$5 + 3 = 3x - 2x$
$x = 8$
将$x = 8$代入$\frac{x}{2}+\frac{m}{3}= x - 4$
$\frac{8}{2}+\frac{m}{3}= 8 - 4$
$4 + \frac{m}{3}= 4$
$\frac{m}{3}= 0$
$m = 0$
0
16. 冬冬原计划骑车以每小时12千米的速度从家到博物馆,刚好在规定时间到达,但他因临时有事耽误了20分钟才出发,只好以每小时15千米的速度前进,结果在规定时间前4分钟到达,则冬冬家距博物馆
24
千米.答案:24
解析:
解:设冬冬家距博物馆$x$千米,规定时间为$t$小时。
根据原计划,$x = 12t$。
耽误20分钟(即$\frac{20}{60} = \frac{1}{3}$小时)出发,以15千米/小时的速度前进,结果提前4分钟(即$\frac{4}{60} = \frac{1}{15}$小时)到达,所用时间为$t - \frac{1}{3} - \frac{1}{15}$小时,可得$x = 15\left(t - \frac{1}{3} - \frac{1}{15}\right)$。
联立方程:$12t = 15\left(t - \frac{1}{3} - \frac{1}{15}\right)$
化简右边:$15\left(t - \frac{5}{15} - \frac{1}{15}\right) = 15\left(t - \frac{6}{15}\right) = 15t - 6$
则$12t = 15t - 6$
$3t = 6$
$t = 2$
所以$x = 12t = 12×2 = 24$
24
根据原计划,$x = 12t$。
耽误20分钟(即$\frac{20}{60} = \frac{1}{3}$小时)出发,以15千米/小时的速度前进,结果提前4分钟(即$\frac{4}{60} = \frac{1}{15}$小时)到达,所用时间为$t - \frac{1}{3} - \frac{1}{15}$小时,可得$x = 15\left(t - \frac{1}{3} - \frac{1}{15}\right)$。
联立方程:$12t = 15\left(t - \frac{1}{3} - \frac{1}{15}\right)$
化简右边:$15\left(t - \frac{5}{15} - \frac{1}{15}\right) = 15\left(t - \frac{6}{15}\right) = 15t - 6$
则$12t = 15t - 6$
$3t = 6$
$t = 2$
所以$x = 12t = 12×2 = 24$
24
17. 延长线段$AB到点C$,使$BC= \frac{1}{3}AB$,反向延长线段$AB到点D$,使$AD= \frac{1}{2}AC$,$E为AB$的中点,$F为CD$的中点. 若$AB = 12cm$,则线段$EF$的长为
2
$cm$.答案:2
解析:
解:
∵AB=12cm,
∴BC=1/3AB=4cm,AC=AB+BC=16cm,
AD=1/2AC=8cm,DB=AD+AB=20cm,DC=DB+BC=24cm,
∵E为AB中点,F为CD中点,
∴AE=1/2AB=6cm,DF=1/2DC=12cm,
∴DE=AD+AE=14cm,EF=DF-DE=12-14=-2(取绝对值)=2cm。
答案:2
∵AB=12cm,
∴BC=1/3AB=4cm,AC=AB+BC=16cm,
AD=1/2AC=8cm,DB=AD+AB=20cm,DC=DB+BC=24cm,
∵E为AB中点,F为CD中点,
∴AE=1/2AB=6cm,DF=1/2DC=12cm,
∴DE=AD+AE=14cm,EF=DF-DE=12-14=-2(取绝对值)=2cm。
答案:2
18. 传说“九宫图”是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”. 数学中的“九宫图”所体现的是一个$3×3$表格,每行、每列、每条斜对角线上的三个数之和都相等,也称为三阶幻方. 如图所示为一个满足上述条件的三阶幻方的一部分,则$m$表示的数是
12
.答案:12