1. 比较两个角大小的两种常用方法是
叠合法
和度量法
.答案:叠合法 度量法
2. 角的平分线:
(1) 概念:一般地,从一个角的顶点出发,把这个角分成两个
(2) 符号语言:如图,因为 $ OC $ 是 $ \angle AOB $ 的平分线,所以
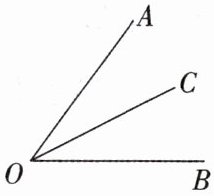
(1) 概念:一般地,从一个角的顶点出发,把这个角分成两个
相等
的角的射线
,叫作这个角的平分线.(2) 符号语言:如图,因为 $ OC $ 是 $ \angle AOB $ 的平分线,所以
$\angle AOC$
=$\angle BOC$
= $ \frac{1}{2}\angle AOB $ 或 $ \angle AOB = 2 $$\angle AOC$
= $ 2 $$\angle BOC$
.
答案:(1) 相等 射线 (2) $\angle AOC$ $\angle BOC$ $\angle AOC$ $\angle BOC$
1. 如图,把一副三角尺叠合在一起,则 $ \angle AOB $ 的度数为 (

A.$ 15^{\circ} $
B.$ 20^{\circ} $
C.$ 30^{\circ} $
D.$ 70^{\circ} $
A
) 
A.$ 15^{\circ} $
B.$ 20^{\circ} $
C.$ 30^{\circ} $
D.$ 70^{\circ} $
答案:A
解析:
解:一副三角尺的锐角分别为 30°、60°和 45°、45°。由图可知,$\angle AOB$ 是 45°角与 30°角的差,即 $45^{\circ} - 30^{\circ} = 15^{\circ}$。
答案:A
答案:A
2. 如图,$ \angle AOB = 68^{\circ} $,$ OC $ 平分 $ \angle AOD $,$ \angle COD = 15^{\circ} $,则 $ \angle BOD $ 的度数为 (

A.$ 28^{\circ} $
B.$ 38^{\circ} $
C.$ 48^{\circ} $
D.$ 53^{\circ} $
B
)
A.$ 28^{\circ} $
B.$ 38^{\circ} $
C.$ 48^{\circ} $
D.$ 53^{\circ} $
答案:B
解析:
解:∵OC平分∠AOD,∠COD=15°
∴∠AOD=2∠COD=2×15°=30°
∵∠AOB=68°
∴∠BOD=∠AOB - ∠AOD=68° - 30°=38°
答案:B
∴∠AOD=2∠COD=2×15°=30°
∵∠AOB=68°
∴∠BOD=∠AOB - ∠AOD=68° - 30°=38°
答案:B
3. 如图,射线 $ OA $ 表示的方位角是南偏东 $ 25^{\circ} $,射线 $ OB $ 与射线 $ OA $ 构成平角,那么射线 $ OB $ 所表示的方位角是
北偏西 $25^{\circ}$
.答案:北偏西 $25^{\circ}$
解析:
解:因为射线 $OA$ 表示南偏东 $25^{\circ}$,射线 $OB$ 与射线 $OA$ 构成平角,所以射线 $OB$ 与射线 $OA$ 方向相反。南偏东的相反方向是北偏西,角度不变,故射线 $OB$ 所表示的方位角是北偏西 $25^{\circ}$。
北偏西 $25^{\circ}$
北偏西 $25^{\circ}$
4. 如图,$ \angle AOB = 57^{\circ} $,$ \angle BOC = 20^{\circ}18' $,则 $ \angle AOC $ 的度数为
$36^{\circ}42'$
.答案:$36^{\circ}42'$
解析:
解:由图可知,点C在∠AOB内部,
∠AOC = ∠AOB - ∠BOC
= 57° - 20°18'
= 56°60' - 20°18'
= 36°42'
36°42'
∠AOC = ∠AOB - ∠BOC
= 57° - 20°18'
= 56°60' - 20°18'
= 36°42'
36°42'
5. 计算:
(1) $ 153^{\circ}29'42'' + 26^{\circ}40'32'' $;
(2) $ 62^{\circ}24'17'' × 4 $.
(1) $ 153^{\circ}29'42'' + 26^{\circ}40'32'' $;
(2) $ 62^{\circ}24'17'' × 4 $.
答案:(1) $153^{\circ}29'42'' + 26^{\circ}40'32''$
$=(153^{\circ}+26^{\circ})+(29'+40')+(42''+32'')$
$=179^{\circ}+69'+74''$
$=179^{\circ}+1^{\circ}9'+1'14''$
$=180^{\circ}10'14''$
(2) $62^{\circ}24'17''×4$
$=62^{\circ}×4 + 24'×4 + 17''×4$
$=248^{\circ}+96'+68''$
$=248^{\circ}+1^{\circ}36'+1'8''$
$=249^{\circ}37'8''$
$=(153^{\circ}+26^{\circ})+(29'+40')+(42''+32'')$
$=179^{\circ}+69'+74''$
$=179^{\circ}+1^{\circ}9'+1'14''$
$=180^{\circ}10'14''$
(2) $62^{\circ}24'17''×4$
$=62^{\circ}×4 + 24'×4 + 17''×4$
$=248^{\circ}+96'+68''$
$=248^{\circ}+1^{\circ}36'+1'8''$
$=249^{\circ}37'8''$
解析:
(1) $153^{\circ}29'42'' + 26^{\circ}40'32''$
$=(153^{\circ}+26^{\circ})+(29'+40')+(42''+32'')$
$=179^{\circ}+69'+74''$
$=179^{\circ}+1^{\circ}9'+1'14''$
$=180^{\circ}10'14''$
(2) $62^{\circ}24'17''×4$
$=62^{\circ}×4 + 24'×4 + 17''×4$
$=248^{\circ}+96'+68''$
$=248^{\circ}+1^{\circ}36'+1'8''$
$=249^{\circ}37'8''$
$=(153^{\circ}+26^{\circ})+(29'+40')+(42''+32'')$
$=179^{\circ}+69'+74''$
$=179^{\circ}+1^{\circ}9'+1'14''$
$=180^{\circ}10'14''$
(2) $62^{\circ}24'17''×4$
$=62^{\circ}×4 + 24'×4 + 17''×4$
$=248^{\circ}+96'+68''$
$=248^{\circ}+1^{\circ}36'+1'8''$
$=249^{\circ}37'8''$
6. 如图,$ OC $ 是 $ \angle AOB $ 的平分线,$ \angle COD = 20^{\circ} $.
(1) 若 $ \angle AOD = 30^{\circ} $,求 $ \angle AOB $ 的度数;
(2) 若 $ \angle BOD = 2\angle AOD $,求 $ \angle AOB $ 的度数.

(1) 若 $ \angle AOD = 30^{\circ} $,求 $ \angle AOB $ 的度数;
(2) 若 $ \angle BOD = 2\angle AOD $,求 $ \angle AOB $ 的度数.

答案:(1) 因为 $\angle COD = 20^{\circ}$,$\angle AOD = 30^{\circ}$,所以 $\angle AOC = \angle COD + \angle AOD = 20^{\circ} + 30^{\circ} = 50^{\circ}$。因为 $OC$ 是 $\angle AOB$ 的平分线,所以 $\angle AOB = 2\angle AOC = 100^{\circ}$ (2) 设 $\angle AOD = x$,则 $\angle BOD = 2x$,所以 $\angle AOB = \angle AOD + \angle BOD = 3x$。因为 $OC$ 是 $\angle AOB$ 的平分线,所以 $\angle AOC = \frac{1}{2}\angle AOB = \frac{3}{2}x$。因为 $\angle COD = 20^{\circ}$,所以 $\frac{3}{2}x - x = 20^{\circ}$,解得 $x = 40^{\circ}$。所以 $\angle AOB = 3x = 120^{\circ}$