12. 若一个常见几何体模型共有8条棱,则该几何体的名称是
四棱锥
.答案：四棱锥 [解析]这个常见几何体共有8条棱，所以这个几何体是四棱锥.
13. 用一个平面去截一个几何体,若截面(截出的面)的形状是四边形,则这个几何体可以是：①三棱柱；②三棱锥；③长方体；④圆柱.其中所有正确结论的序号是
①②③④
.答案：①②③④
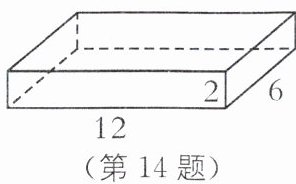
14. 如图,有两个相同的长方体纸盒,它们的长、宽、高分别是12 cm,6 cm,2 cm,现要用这两个纸盒搭成一个大长方体,搭成的大长方体的表面积最小为$ cm^2.$
答案：
288 [解析]图
(1)中，长方体的高为4cm，则表面积=2×(12×6+12×4+4×6)=288(cm²);图
(2)中，长为24cm，则表面积=2×(24×6+24×2+6×2)=408(cm²);图
(3)中，宽为12cm，则表面积=2×(12×12+12×2+12×2)=384(cm²).
∴图
(1)的表面积最小，最小表面积为288cm².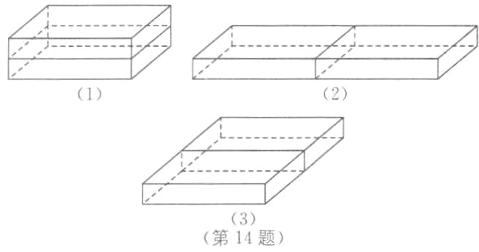
思路引导 两个长方体搭成一个长方体，只要重合的一面越大，大长方体的表面积越小，只需计算图
(1).
288 [解析]图
(1)中，长方体的高为4cm，则表面积=2×(12×6+12×4+4×6)=288(cm²);图
(2)中，长为24cm，则表面积=2×(24×6+24×2+6×2)=408(cm²);图
(3)中，宽为12cm，则表面积=2×(12×12+12×2+12×2)=384(cm²).
∴图
(1)的表面积最小，最小表面积为288cm².
思路引导 两个长方体搭成一个长方体，只要重合的一面越大，大长方体的表面积越小，只需计算图(1).
15. 如图是小明同学在数学实践课上,所设计的正方体盒子的平面展开图.每个面上都有一个汉字,请你判断,正方体盒子上与“善”字相对的面上的字是
文
.答案：文
16. 如图是一个正方体的表面展开图,每个面上都标有字母.其中与字母A处于正方体相对面上的是字母
F
.答案：F
17. 如图,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之积为12,则x－y＝
3
.答案：3
解析：
在正方体的平面展开图中，相对面之间一定相隔一个正方形。
由图可知，“2”与“x”是相对面，“4”与“y”是相对面。
因为相对面上两个数之积为12，所以：
$2x = 12$，解得$x = 6$；
$4y = 12$，解得$y = 3$。
则$x - y = 6 - 3 = 3$。
3
由图可知，“2”与“x”是相对面，“4”与“y”是相对面。
因为相对面上两个数之积为12，所以：
$2x = 12$，解得$x = 6$；
$4y = 12$，解得$y = 3$。
则$x - y = 6 - 3 = 3$。
3
18. 如图(1)是边长为1的六个小正方形组成的图形,它可以围成如图(2)的正方体,则图(1)中小正方形顶点A,B在围成的正方体上的距离是
1
.答案：1
19. 如图,上面的每个平面图形经过旋转得到下面的一个几何体,用线连接起来.
答案：
如图所示：
如图所示：
20.(2025·山东淄博期末)小明在学习了《展开与折叠》这一课后,掌握了长方体盒子的制作方法.如图是他制作的一个半成品的平面图.
(1)在图中补充一个长方形,使该平面图能折叠成一个长方体盒子；
(2)已知小明制作长方体的盒子长是宽的2倍,宽是高的2倍,且长方体所有棱长的和为56 cm,求这个长方体盒子的体积.
(1)在图中补充一个长方形,使该平面图能折叠成一个长方体盒子；
(2)已知小明制作长方体的盒子长是宽的2倍,宽是高的2倍,且长方体所有棱长的和为56 cm,求这个长方体盒子的体积.
答案：
(1)如图所示(答案不唯一).
(2)设长方体盒子的高为a cm，则宽为2a cm，长为4a cm，根据题意，得4(a+2a+4a)=56，解得a=2，
∴这个长方体盒子的高为2cm，宽为4cm，长为8cm，
∴这个长方体盒子的体积为2×4×8=64(cm³).
(1)如图所示(答案不唯一).
(2)设长方体盒子的高为a cm，则宽为2a cm，长为4a cm，根据题意，得4(a+2a+4a)=56，解得a=2，
∴这个长方体盒子的高为2cm，宽为4cm，长为8cm，
∴这个长方体盒子的体积为2×4×8=64(cm³).
21.(2024·宿迁沭阳月考)如图,用经过A,B,C三点的平面截去正方体的一角,剩下部分是一个新的多面体,若这个多面体的面数为m,棱数为n,求m＋n的值.
答案：
∵正方体有6个面，被截去了一个角，增加了1个面，
∴新的多面体有7个面，故m=7.
∵正方体有12条棱，被截去了3条棱，截面为三角形，
∴增加了3条棱，故棱数不变，即n=12，
∴m+n=7+12=19.
∵正方体有6个面，被截去了一个角，增加了1个面，
∴新的多面体有7个面，故m=7.
∵正方体有12条棱，被截去了3条棱，截面为三角形，
∴增加了3条棱，故棱数不变，即n=12，
∴m+n=7+12=19.