7. (2025·南通海安期末)中国古代数学著作《增删算法统宗》中记载的“绳索量竿”问题,大意是:现有一根竿子和一条绳索,用绳索去量竿子,绳索比竿子长5尺;若将绳索对折去量竿子,绳索就比竿子短5尺,问绳索、竿子各有多长?甲、乙两人所列方程如下,下列选项判断正确的是(
甲:设竿子长为x尺,根据题意可列方程为$x-\frac{x+5}{2}= 5$;
乙:设绳索长为x尺,根据题意可列方程为$(x-5)-\frac{x}{2}= 5$.
A.甲对乙错
B.甲错乙对
C.甲、乙都对
D.甲、乙都错
C
).甲:设竿子长为x尺,根据题意可列方程为$x-\frac{x+5}{2}= 5$;
乙:设绳索长为x尺,根据题意可列方程为$(x-5)-\frac{x}{2}= 5$.
A.甲对乙错
B.甲错乙对
C.甲、乙都对
D.甲、乙都错
答案:C [解析]甲:设竿子长为x尺,根据“若将绳索对折去量竿子,绳索就比竿子短5尺”可列方程为x-$\frac{x+5}{2}$=5;乙:设绳索长为x尺,根据“若将绳索对折去量竿子,绳索就比竿子短5尺”可列方程为(x-5)-$\frac{x}{2}$=5,
∴甲、乙都对.故选C.
∴甲、乙都对.故选C.
8. (2025·连云港东海期末)程大位是我国珠算发明家,他完成的杰作《直指算法统宗》是东方古代数学名著,在书中记载了一道趣题:一百个馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?如果设大和尚有x人,根据题意可列方程为(
A.$3x= 100-\frac{1}{3}x$
B.$\frac{1}{3}x+100-3x= 100$
C.$3x+\frac{1}{3}(100-x)= 100$
D.$\frac{1}{3}x+3(100-x)= 100$
C
).A.$3x= 100-\frac{1}{3}x$
B.$\frac{1}{3}x+100-3x= 100$
C.$3x+\frac{1}{3}(100-x)= 100$
D.$\frac{1}{3}x+3(100-x)= 100$
答案:C
解析:
设大和尚有$x$人,则小和尚有$(100 - x)$人。
大和尚分得馒头数为$3x$个,小和尚分得馒头数为$\frac{1}{3}(100 - x)$个。
根据馒头总数为100个,可列方程:$3x+\frac{1}{3}(100 - x)=100$。
C
大和尚分得馒头数为$3x$个,小和尚分得馒头数为$\frac{1}{3}(100 - x)$个。
根据馒头总数为100个,可列方程:$3x+\frac{1}{3}(100 - x)=100$。
C
9. 某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更划算?请写出你做出这种决策的理由.
(1)该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更划算?请写出你做出这种决策的理由.
答案:
(1)设客房有x间.根据题意,得7x+7=9x-9,解得x=8,所以房客为7×8+7=63(人).故该店有客房8间,房客63人.
(2)如果每4人一个房间,需要63÷4=15$\frac{3}{4}$≈16间客房,总费用为16×20=320(钱).若定18间,则总费用为18×20×0.8=288(钱)<320钱.故他们再次入住定18间房时更划算.
归纳总结 本题考查了一元一次方程的应用,熟练掌握一元一次方程的解题方法是解题的关键.
(1)设客房有x间.根据题意,得7x+7=9x-9,解得x=8,所以房客为7×8+7=63(人).故该店有客房8间,房客63人.
(2)如果每4人一个房间,需要63÷4=15$\frac{3}{4}$≈16间客房,总费用为16×20=320(钱).若定18间,则总费用为18×20×0.8=288(钱)<320钱.故他们再次入住定18间房时更划算.
归纳总结 本题考查了一元一次方程的应用,熟练掌握一元一次方程的解题方法是解题的关键.
10. (2025·徐州三十六中期末)如图,一束平行光线照射平面镜后反射,若入射光线与平面镜夹角∠1= 50°,则反射光线与平面镜夹角∠4的度数为
50°
.答案:50°
11. (2025·连云港月考)我们知道乌鸦喝水的故事.现在来做一个道理相同的游戏.如图,在圆柱形玻璃桶里已有定量的水,将大小相同的围棋棋子一个个慢慢投入其中.显然,在有水溢出之前,每投入一个棋子,桶里水位的高度都会有变化.根据如图信息,解答下列各题: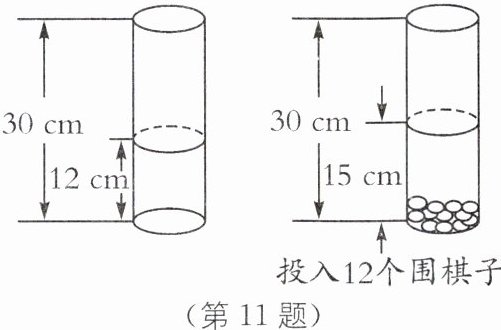
(1)投入第1个围棋子后,水位上升了
(2)设投入了n个围棋子,没有水溢出.用n表示此时桶里水的高度.
(3)小亮认为投入72个围棋子,正好可使水位达到桶的高度.你同意他的观点吗?说说理由.

(1)投入第1个围棋子后,水位上升了
0.25
cm,此时桶里的水位高度达到了12.25
cm.(2)设投入了n个围棋子,没有水溢出.用n表示此时桶里水的高度.
桶里水的高度为(0.25n+12)cm.
(3)小亮认为投入72个围棋子,正好可使水位达到桶的高度.你同意他的观点吗?说说理由.
同意.理由如下:∵当n=72时,0.25n+12=30,∴正好可使水位达到桶的高度.
答案:
(1)0.25 12.25 [解析]无棋子时,水位为12cm,投入12个围棋子时,水位增长了3cm,所以每增加一个棋子,水位上升3÷12=0.25(cm).故投入第1个围棋子后,水位上升了0.25cm,此时桶里的水位高度达到了12.25cm.
(2)由
(1)知,每增加一个围棋子,水位上升0.25cm.故桶里水的高度为(0.25n+12)cm.
(3)同意.理由如下:
∵当n=72时,0.25n+12=30,
∴正好可使水位达到桶的高度.
(1)0.25 12.25 [解析]无棋子时,水位为12cm,投入12个围棋子时,水位增长了3cm,所以每增加一个棋子,水位上升3÷12=0.25(cm).故投入第1个围棋子后,水位上升了0.25cm,此时桶里的水位高度达到了12.25cm.
(2)由
(1)知,每增加一个围棋子,水位上升0.25cm.故桶里水的高度为(0.25n+12)cm.
(3)同意.理由如下:
∵当n=72时,0.25n+12=30,
∴正好可使水位达到桶的高度.