1. 中考新考法 证明代数结论 (2025·浙江绍兴越城区期末)
日常生活中,我们常常将“八点五十五分”说成“九点差五分”,有时这样表达更清楚. 这就启发我们设计了一种新的加减记数法. 例如:9 可写成$1\overline{1}$,$1\overline{1}= 10-1$;198 可写成$20\overline{2}$,$20\overline{2}= 200-2$;7683 可写成$\overline{1232}3$,$\overline{1232}3= 10000-2320+3$. 总之,数字上画一杠表示减去“它”,按这个方法计算:$5\overline{23}\overline{1}-3\overline{24}1= $
日常生活中,我们常常将“八点五十五分”说成“九点差五分”,有时这样表达更清楚. 这就启发我们设计了一种新的加减记数法. 例如:9 可写成$1\overline{1}$,$1\overline{1}= 10-1$;198 可写成$20\overline{2}$,$20\overline{2}= 200-2$;7683 可写成$\overline{1232}3$,$\overline{1232}3= 10000-2320+3$. 总之,数字上画一杠表示减去“它”,按这个方法计算:$5\overline{23}\overline{1}-3\overline{24}1= $
2068
.答案:2 068 [解析]523ˉ¹-324ˉ¹=(5 000-200)+(30-1)-[3 000-240+1]=4 800+29-2 761=4 829-2 761=2 068. 归纳总结 本题主要考查有理数的混合运算,解答的关键是理解清楚所给的记数方式.
2. 计算:
(1)$-5-(-3)+(-4)-[-(-2)]$;
(2)$\frac{2}{3}+(\frac{5}{6}+2.8+\frac{1}{3})-(2\frac{4}{5}+\frac{5}{6})$;
(3)$-(-\frac{3}{2})+(-\frac{5}{6})+[\frac{11}{4}-(-\frac{3}{8})-(+\frac{14}{3})]$.
(1)$-5-(-3)+(-4)-[-(-2)]$;
(2)$\frac{2}{3}+(\frac{5}{6}+2.8+\frac{1}{3})-(2\frac{4}{5}+\frac{5}{6})$;
(3)$-(-\frac{3}{2})+(-\frac{5}{6})+[\frac{11}{4}-(-\frac{3}{8})-(+\frac{14}{3})]$.
答案:
(1)原式=-5+3-4-2=-8.
(2)原式=$\frac{2}{3}+\frac{5}{6}+2.8+\frac{1}{3}-2\frac{4}{5}-\frac{5}{6}=1$.
(3)原式=$\frac{3}{2}-\frac{5}{6}+\frac{11}{4}+\frac{3}{8}-\frac{14}{3}$
=$\frac{36}{24}-\frac{20}{24}+\frac{66}{24}+\frac{9}{24}-\frac{112}{24}$
=$\frac{36-20+66+9-112}{24}=-\frac{7}{8}$.
(1)原式=-5+3-4-2=-8.
(2)原式=$\frac{2}{3}+\frac{5}{6}+2.8+\frac{1}{3}-2\frac{4}{5}-\frac{5}{6}=1$.
(3)原式=$\frac{3}{2}-\frac{5}{6}+\frac{11}{4}+\frac{3}{8}-\frac{14}{3}$
=$\frac{36}{24}-\frac{20}{24}+\frac{66}{24}+\frac{9}{24}-\frac{112}{24}$
=$\frac{36-20+66+9-112}{24}=-\frac{7}{8}$.
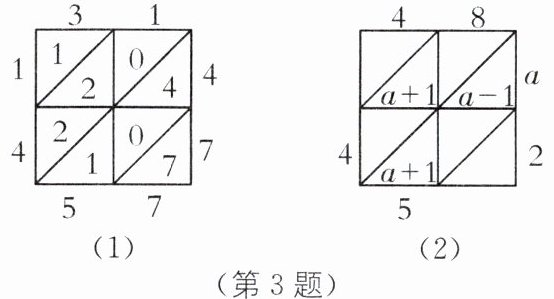
3. 传统文化 “铺地锦” 我国明朝数学家程大位所著的《算法统宗》中介绍了一种计算乘法的方法,称为“铺地锦”. 例如,如图(1)所示,计算$31×47$,首先把乘数 31 和 47 分别写在方格的上面和右面,然后以 31 的每位数字分别乘 47 的每位数字,将结果计入对应的格子中(如$3×4= 12$的 12 写在 3 下面的方格里,十位 1 写在斜线的上面,个位 2 写在斜线的下面),再把同一斜线上的数相加,结果写在斜线末端,最后把得数依次写下来是 1457,即$31×47= 1457$. 如图(2),用“铺地锦”的方法表示两个两位数相乘,则a的值是(
A.2
B.3
C.5
D.7
D
).
A.2
B.3
C.5
D.7
答案:D
解析:
由题意知,上方乘数为48,右方乘数为$10a + 2$。
左上角格子:$4× a = a + 1$(十位)和下方数字(个位),即$4a = 10(a + 1) + 个位数字$,因$4a$为两位数,设个位数字为$b$,则$4a = 10(a + 1) + b$,但结合右上角格子$8× a = a - 1$(十位)和个位数字,$8a = 10(a - 1) + c$($c$为个位),且同一斜线相加:
右下角斜线:$8× 2$的个位数字为结果个位,$8× 2 = 16$,个位为6。
中间斜线:$4× 2$的个位数字$8$、$8× a$的个位数字$c$、$4× a$的个位数字$b$相加得5(十位),即$8 + c + b = 15$(向百位进1)。
左上角斜线:$4× a$的十位$a + 1$、$8× a$的十位$a - 1$相加加进位1得结果百位以上,即$(a + 1) + (a - 1) + 1 = 4 + a$(因$48×(10a + 2)$的千位为4),解得$2a + 1 = 4 + a$,$a = 3$。
验证:$a = 3$时,右方乘数为32,$48×32 = 1536$,铺地锦格子符合:$4×3 = 12$($a + 1 = 4$错误,应为$a + 1 = 4$是十位1,个位2;$8×3 = 24$($a - 1 = 2$十位2,个位4),中间斜线$8 + 4 + 2 = 14$,写4进1,左上角$1 + 2 + 1 = 4$,结果1536正确。
D
左上角格子:$4× a = a + 1$(十位)和下方数字(个位),即$4a = 10(a + 1) + 个位数字$,因$4a$为两位数,设个位数字为$b$,则$4a = 10(a + 1) + b$,但结合右上角格子$8× a = a - 1$(十位)和个位数字,$8a = 10(a - 1) + c$($c$为个位),且同一斜线相加:
右下角斜线:$8× 2$的个位数字为结果个位,$8× 2 = 16$,个位为6。
中间斜线:$4× 2$的个位数字$8$、$8× a$的个位数字$c$、$4× a$的个位数字$b$相加得5(十位),即$8 + c + b = 15$(向百位进1)。
左上角斜线:$4× a$的十位$a + 1$、$8× a$的十位$a - 1$相加加进位1得结果百位以上,即$(a + 1) + (a - 1) + 1 = 4 + a$(因$48×(10a + 2)$的千位为4),解得$2a + 1 = 4 + a$,$a = 3$。
验证:$a = 3$时,右方乘数为32,$48×32 = 1536$,铺地锦格子符合:$4×3 = 12$($a + 1 = 4$错误,应为$a + 1 = 4$是十位1,个位2;$8×3 = 24$($a - 1 = 2$十位2,个位4),中间斜线$8 + 4 + 2 = 14$,写4进1,左上角$1 + 2 + 1 = 4$,结果1536正确。
D
4. 计算:
(1)$[2\frac{1}{2}-(-1\frac{1}{2})]÷(-\frac{1}{4})×(-\frac{1}{8})$;
(2)$18÷\left\{1\frac{5}{12}-\left[2\frac{4}{5}÷(-3\frac{9}{25})-0.75\right]\right\}$.
(1)$[2\frac{1}{2}-(-1\frac{1}{2})]÷(-\frac{1}{4})×(-\frac{1}{8})$;
(2)$18÷\left\{1\frac{5}{12}-\left[2\frac{4}{5}÷(-3\frac{9}{25})-0.75\right]\right\}$.
答案:
(1)原式=4×(-4)×$(-\frac{1}{8})=2$.
(2)原式=18÷$(1\frac{5}{12}+2\frac{4}{5}÷3\frac{9}{25}+\frac{3}{4})$
=18÷$(1\frac{5}{12}+\frac{5}{6}+\frac{3}{4})=18÷3=6$.
(1)原式=4×(-4)×$(-\frac{1}{8})=2$.
(2)原式=18÷$(1\frac{5}{12}+2\frac{4}{5}÷3\frac{9}{25}+\frac{3}{4})$
=18÷$(1\frac{5}{12}+\frac{5}{6}+\frac{3}{4})=18÷3=6$.