7. 中考新考法 满足条件的结论开放 (2024·包头中考改编)在平面直角坐标系中,若一次函数的图象经过第一、三象限,请写出一个符合该条件的正比例函数的表达式______.
y=x(答案不唯一)
答案:$y=x$(答案不唯一) [解析]令正比例函数的表达式为$y=kx(k≠0)$,因为正比例函数的图象经过第一、三象限,所以$k>0$,则正比例函数的表达式可以是$y=x$.
8. (2025·扬州广陵区期末)如图,平面直角坐标系中,$OB= OC= OA$,$B(0,1)$,$A$,$C$ 分别在 $x$ 轴的正、负半轴上. 过点 $C$ 的直线绕点 $C$ 旋转,交 $y$ 轴于点 $D$,交线段 $AB$ 于点 $E$.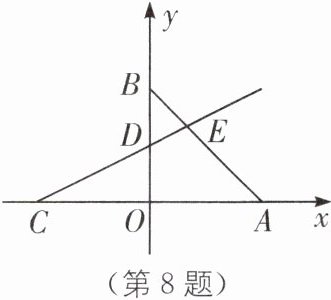
(1)直接写出 $A$,$C$ 的坐标;
(2)写出直线 $AB$ 的表达式;
(3)若 $\triangle OCD$ 与 $\triangle BDE$ 的面积相等,求点 $E$ 的坐标.

(1)直接写出 $A$,$C$ 的坐标;
(2)写出直线 $AB$ 的表达式;
(3)若 $\triangle OCD$ 与 $\triangle BDE$ 的面积相等,求点 $E$ 的坐标.
答案:
(1)
∵$OB=OC=OA$,$B(0,1)$,
∴$OC=OA=1$.
∵$A$,$C$分别在x轴的正、负半轴上,
∴$A(1,0)$,$C(-1,0)$.
(2)设直线AB的表达式为$y=kx+b$,把$A(1,0)$,$B(0,1)$代入,得$\begin{cases}k + b = 0\\b = 1\end{cases}$,解得$\begin{cases}k = -1\\b = 1\end{cases}$,
∴直线AB的表达式为$y=-x+1$.
(3)设$E(m,-m+1)$,
∵$S_{\triangle OCD}=S_{\triangle BDE}$,
∴$S_{\triangle ECA}=S_{\triangle BOA}$,
∴$\frac{1}{2}AC\cdot y_{E}=\frac{1}{2}OA\cdot OB$,
∴$\frac{1}{2}×(OA + OC)\cdot (-m + 1)=\frac{1}{2}×1×1$,解得$m=\frac{1}{2}$,
∴$-m + 1=-\frac{1}{2}+1=\frac{1}{2}$,
∴点E的坐标为$(\frac{1}{2},\frac{1}{2})$.
(1)
∵$OB=OC=OA$,$B(0,1)$,
∴$OC=OA=1$.
∵$A$,$C$分别在x轴的正、负半轴上,
∴$A(1,0)$,$C(-1,0)$.
(2)设直线AB的表达式为$y=kx+b$,把$A(1,0)$,$B(0,1)$代入,得$\begin{cases}k + b = 0\\b = 1\end{cases}$,解得$\begin{cases}k = -1\\b = 1\end{cases}$,
∴直线AB的表达式为$y=-x+1$.
(3)设$E(m,-m+1)$,
∵$S_{\triangle OCD}=S_{\triangle BDE}$,
∴$S_{\triangle ECA}=S_{\triangle BOA}$,
∴$\frac{1}{2}AC\cdot y_{E}=\frac{1}{2}OA\cdot OB$,
∴$\frac{1}{2}×(OA + OC)\cdot (-m + 1)=\frac{1}{2}×1×1$,解得$m=\frac{1}{2}$,
∴$-m + 1=-\frac{1}{2}+1=\frac{1}{2}$,
∴点E的坐标为$(\frac{1}{2},\frac{1}{2})$.
9. 分段收费问题 小明家所在地的供电公司实行“峰谷电价”,峰时($8:00~21:00$)电价为 0.5 元/千瓦时,谷时($21:00~8:00$)电价为 0.3 元/千瓦时. 为了解空调制暖的耗能情况,小明记录了家里某天 0 时~24 时内空调制暖的用电量,其用电量 $y$(千瓦时)与时间 $x$(h)的函数关系如图所示.
(1)小明家白天不开空调的时间共______h;
(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为 $w$ 元,请画出该天 0 时~24 时内 $w$ 与 $x$ 的函数图象.(标注必要数据)

(1)小明家白天不开空调的时间共______h;
(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为 $w$ 元,请画出该天 0 时~24 时内 $w$ 与 $x$ 的函数图象.(标注必要数据)
答案:
(1)10 [解析]小明家白天不开空调的时间为$18 - 8 = 10$(h).
(2)平均每小时用电量为3千瓦时,峰时所用电费为$(21 - 18)×3×0.5 = 4.5$(元),谷时所用电费为$(24 - 21 + 8)×3×0.3 = 9.9$(元),
∴小明家该天空调制暖所用电费为$4.5 + 9.9 = 14.4$(元).
(3)根据题意,可得该天0时~24时内w与x的函数图象如图所示: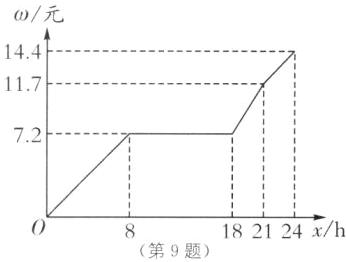
(1)10 [解析]小明家白天不开空调的时间为$18 - 8 = 10$(h).
(2)平均每小时用电量为3千瓦时,峰时所用电费为$(21 - 18)×3×0.5 = 4.5$(元),谷时所用电费为$(24 - 21 + 8)×3×0.3 = 9.9$(元),
∴小明家该天空调制暖所用电费为$4.5 + 9.9 = 14.4$(元).
(3)根据题意,可得该天0时~24时内w与x的函数图象如图所示:

其中正确结论的个数是(
C
).答案:C [解析]
(1)体育场离该同学家2.5km.故
(1)是正确的;
(2)该同学在体育场锻炼的时间为$30 - 15 = 15$(min).故
(2)是正确的;
(3)该同学跑步的平均速度:步行平均速度=$(65 - 30)÷15 > 2$.故
(3)是错误的;
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,则$a÷(103 - 88)=1.5×\frac{2.5}{15}$,解得$a = 3.75$.故
(4)是正确的.故选C.
(1)体育场离该同学家2.5km.故
(1)是正确的;
(2)该同学在体育场锻炼的时间为$30 - 15 = 15$(min).故
(2)是正确的;
(3)该同学跑步的平均速度:步行平均速度=$(65 - 30)÷15 > 2$.故
(3)是错误的;
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,则$a÷(103 - 88)=1.5×\frac{2.5}{15}$,解得$a = 3.75$.故
(4)是正确的.故选C.