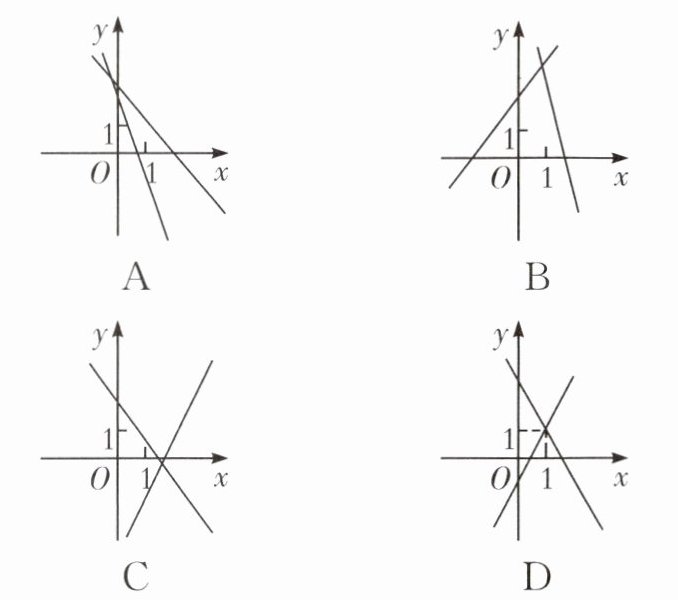
1.(2025·宿迁沭阳期末)在同一平面直角坐标系中,一次函数$y= ax+a^2与y= a^2x+a$的图象可能是(
D
).
答案:D [解析]
∵y=ax+a²与y=a²x+a,
∴x=1时,两函数的值都是a²+a,
∴两直线的交点的横坐标为1.若a>0,则一次函数y=ax+a²与y=a²x+a都是增函数,且都交y轴的正半轴,图象都经过第一、二、三象限;若a<0,则一次函数y=ax+a²经过第一、二、四象限,y=a²x+a经过第一、三、四象限,且两直线的交点的横坐标为1. 故选 D.归纳总结 本题考查一次函数的图象,解题的关键是正确理解k与b的值对直线位置的影响.
∵y=ax+a²与y=a²x+a,
∴x=1时,两函数的值都是a²+a,
∴两直线的交点的横坐标为1.若a>0,则一次函数y=ax+a²与y=a²x+a都是增函数,且都交y轴的正半轴,图象都经过第一、二、三象限;若a<0,则一次函数y=ax+a²经过第一、二、四象限,y=a²x+a经过第一、三、四象限,且两直线的交点的横坐标为1. 故选 D.归纳总结 本题考查一次函数的图象,解题的关键是正确理解k与b的值对直线位置的影响.
一次函数$y= 2x-3+b$中,y 随着 x 的增大而
增大
,当$b=$3
时,函数图象经过原点.答案:增大 3
3.(教材 P159 习题 T6·变式)把函数$y= \frac{x}{3}$的图象向
下
平移2
个单位长度,得到函数$y= \frac{x-6}{3}$的图象.答案:下 2(或右 6)
4.(2025·扬州江都区期末)已知 y 与$2x-3$成正比例,且当$x= 3$时,$y= 6$.
(1)求 y 与 x 的函数关系式;
(2)若$y<10$,求 x 的取值范围;
(3)这个函数的图象与 x 轴相交于点 A,与 y 轴相交于点 B,求$\triangle AOB$的面积.
(1)求 y 与 x 的函数关系式;
(2)若$y<10$,求 x 的取值范围;
(3)这个函数的图象与 x 轴相交于点 A,与 y 轴相交于点 B,求$\triangle AOB$的面积.
答案:
(1)
∵y与2x-3成正比例,
∴设y=k(2x-3),把x=3,y=6代入y=k(2x-3)中,得6=k(6-3),解得k=2,
∴y=2(2x-3)=4x-6.
(2)
∵y<10,
∴4x-6<10,解得x<4.
(3)当x=0时,y=4×0-6=0-6=-6,
∴点B的坐标为(0,-6),
∴OB=6.当y=0时,0=4x-6,解得x=3/2,
∴点A的坐标为(3/2,0),
∴OA=3/2,
∴△AOB的面积=1/2 OA·OB=1/2×3/2×6=9/2.
(1)
∵y与2x-3成正比例,
∴设y=k(2x-3),把x=3,y=6代入y=k(2x-3)中,得6=k(6-3),解得k=2,
∴y=2(2x-3)=4x-6.
(2)
∵y<10,
∴4x-6<10,解得x<4.
(3)当x=0时,y=4×0-6=0-6=-6,
∴点B的坐标为(0,-6),
∴OB=6.当y=0时,0=4x-6,解得x=3/2,
∴点A的坐标为(3/2,0),
∴OA=3/2,
∴△AOB的面积=1/2 OA·OB=1/2×3/2×6=9/2.
5.(2023·淄博中考)下列函数图象中,能反映 y 的值始终随 x 值的增大而增大的是(
C
).答案:C [解析]A. 函数具有对称性,在对称轴的左侧,y的值随x值的增大而增大,在对称轴的右侧,y的值随x值的增大而减小,该选项不符合题意;B. 图象分别在第一、三象限内,在各个象限内,y的值随x值增大而减小,该选项不符合题意;C. 图象中,函数y的值随x值的增大而增大,该选项符合题意;D. 图象在y轴左侧是函数y的值随x值的增大而减小,该选项不符合题意. 故选 C.
6.(2024·通辽中考)如图,在同一平面直角坐标系中,一次函数$y= k_1x+b_1与y= k_2x+b_2$(其中$k_1k_2≠0$,$k_1$,$k_2$,$b_1$,$b_2$为常数)的图象分别为直线$l_1$,$l_2$.下列结论正确的是(
]

A
).]

答案:A [解析]由图象,可得b₁=2,b₂=-1(或b₁=-1,b₂=2),k₁>0,k₂>0,
∴b₁+b₂>0,故选项 A 正确,符合题意;b₁b₂<0,故选项 B 错误,不符合题意;k₁+k₂>0,故选项 C 错误,不符合题意;k₁k₂>0,故选项 D 错误,不符合题意. 故选 A.
∴b₁+b₂>0,故选项 A 正确,符合题意;b₁b₂<0,故选项 B 错误,不符合题意;k₁+k₂>0,故选项 C 错误,不符合题意;k₁k₂>0,故选项 D 错误,不符合题意. 故选 A.
7.(2023·陕西中考)在同一平面直角坐标系中,函数$y= ax和y= x+a$(a 为常数,$a<0$)的图象可能是(

D
).
答案:D [解析]
∵a<0,
∴函数y=ax的图象是经过原点的直线,经过第二、四象限,函数y=x+a的图象是经过第一、三、四象限的直线. 故选 D.归纳总结 本题考查了正比例函数的图象、一次函数的图象,解答本题的关键是明确题意,利用正比例函数和一次函数的性质解答.
∵a<0,
∴函数y=ax的图象是经过原点的直线,经过第二、四象限,函数y=x+a的图象是经过第一、三、四象限的直线. 故选 D.归纳总结 本题考查了正比例函数的图象、一次函数的图象,解答本题的关键是明确题意,利用正比例函数和一次函数的性质解答.