8.(湖北黄冈中学自主招生)已知过点$(2,3)$的直线$y= ax+b(a≠0)$不经过第四象限,设$s= a-2b$,则$s$的取值范围是(
A.$\frac{3}{2}≤s<6$
B.$-3<s≤3$
C.$-6<s≤\frac{3}{2}$
D.$\frac{3}{2}≤s≤5$
C
).A.$\frac{3}{2}≤s<6$
B.$-3<s≤3$
C.$-6<s≤\frac{3}{2}$
D.$\frac{3}{2}≤s≤5$
答案:C [解析]
∵过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,
∴a>0,b≥0,将(2,3)代入直线y=ax+b,得3=2a+b,
∴b=3-2a,
∴{a>0,3-2a≥0,解得0<a≤3/2.
∵s=a-2b=a-2×(3-2a)=5a-6,当a=0时,s=-6;当a=3/2时,s=3/2.故-6<s≤3/2. 故选 C.
∵过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,
∴a>0,b≥0,将(2,3)代入直线y=ax+b,得3=2a+b,
∴b=3-2a,
∴{a>0,3-2a≥0,解得0<a≤3/2.
∵s=a-2b=a-2×(3-2a)=5a-6,当a=0时,s=-6;当a=3/2时,s=3/2.故-6<s≤3/2. 故选 C.
9.(湖北武汉外国语学校自主招生)已知实数 a,b,c 满足$a<b<c$,并且$k= \frac{1}{a-b}+\frac{1}{b-c}+\frac{1}{c-a}$,则直线$y= kx+k$一定经过(
A.第一、三、四象限
B.第一、二、四象限
C.第一、二、三象限
D.第二、三、四象限
D
).A.第一、三、四象限
B.第一、二、四象限
C.第一、二、三象限
D.第二、三、四象限
答案:D [解析]
∵a<b<c,
∴c-a>b-a>0,
∴1/(c-a)<1/(b-a).
∵k=1/(a-b)+1/(b-c)+1/(c-a),
∴k=1/(a-b)+1/(b-c)+1/(c-a)<1/(a-b)+1/(b-c)+1/(b-a)=1/(b-c)<0,
∴直线y=kx+k一定经过第二、三、四象限. 故选 D.
∵a<b<c,
∴c-a>b-a>0,
∴1/(c-a)<1/(b-a).
∵k=1/(a-b)+1/(b-c)+1/(c-a),
∴k=1/(a-b)+1/(b-c)+1/(c-a)<1/(a-b)+1/(b-c)+1/(b-a)=1/(b-c)<0,
∴直线y=kx+k一定经过第二、三、四象限. 故选 D.
10.(2024·扬州邗江区期末)点$A(1,m)$,$B(\frac{3}{2},n)在一次函数y= 3x+1$的图象上,则 m
<
n(用“>”“<”或“=”填空).答案:< [解析]
∵k=3>0,
∴y随x的增大而增大.又点A(1,m),B(3/2,n)在一次函数y=3x+1的图象上,且1<3/2,
∴m<n.
∵k=3>0,
∴y随x的增大而增大.又点A(1,m),B(3/2,n)在一次函数y=3x+1的图象上,且1<3/2,
∴m<n.
11. 已知一次函数$y= (2m+4)x+(3-n)$.
(1)当 m,n 是何值时,y 随 x 的增大而增大?
(2)当 m,n 是何值时,函数图象与 y 轴的交点在 x 轴的下方?
(3)当 m,n 是何值时,函数图象经过原点?
(4)当$m= -1$,$n= 2$时,求此函数的图象与两坐标轴的交点坐标.
(5)若函数的图象经过第一、二、三象限,求 m,n 的取值范围.
(1)当 m,n 是何值时,y 随 x 的增大而增大?
(2)当 m,n 是何值时,函数图象与 y 轴的交点在 x 轴的下方?
(3)当 m,n 是何值时,函数图象经过原点?
(4)当$m= -1$,$n= 2$时,求此函数的图象与两坐标轴的交点坐标.
(5)若函数的图象经过第一、二、三象限,求 m,n 的取值范围.
答案:
(1)当m>-2,n为任意实数时,y随x的增大而增大;
(2)当n>3,m≠-2时,函数图象与y轴的交点在x轴的下方;
(3)当m≠-2,n=3时,函数图象经过原点;
(4)此函数的图象与x轴的交点坐标为(-1/2,0),与y轴的交点坐标为(0,1);
(5)m>-2,n<3
(1)当m>-2,n为任意实数时,y随x的增大而增大;
(2)当n>3,m≠-2时,函数图象与y轴的交点在x轴的下方;
(3)当m≠-2,n=3时,函数图象经过原点;
(4)此函数的图象与x轴的交点坐标为(-1/2,0),与y轴的交点坐标为(0,1);
(5)m>-2,n<3
12. 已知一次函数$y= mx-(m-2)$.
(1)若图象过点$(0,3)$,则 m 的值是多少?
(2)若它的图象经过第一、二、四象限,则 m 的取值范围是多少?
(3)若直线不经过第四象限,则 m 的取值范围是多少?
精题详解
(1)若图象过点$(0,3)$,则 m 的值是多少?
(2)若它的图象经过第一、二、四象限,则 m 的取值范围是多少?
(3)若直线不经过第四象限,则 m 的取值范围是多少?
精题详解
答案:
(1)
∵一次函数y=mx-(m-2)的图象过点(0,3),
∴3=-(m-2),解得m=-1.
(2)
∵一次函数y=mx-(m-2)的图象经过第一、二、四象限,
∴{m<0,-(m-2)>0,解得m<0,即m的取值范围是m<0.
(3)
∵一次函数y=mx-(m-2)的图象不经过第四象限,
∴{m>0,-(m-2)≥0,解得0<m≤2,即m的取值范围是0<m≤2
(1)
∵一次函数y=mx-(m-2)的图象过点(0,3),
∴3=-(m-2),解得m=-1.
(2)
∵一次函数y=mx-(m-2)的图象经过第一、二、四象限,
∴{m<0,-(m-2)>0,解得m<0,即m的取值范围是m<0.
(3)
∵一次函数y=mx-(m-2)的图象不经过第四象限,
∴{m>0,-(m-2)≥0,解得0<m≤2,即m的取值范围是0<m≤2
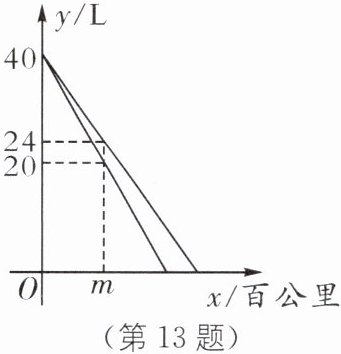
13.(2024·镇江中考)甲、乙两车出发前油箱里都有 40 L 油,油箱剩余油量 y(单位:L)关于行驶路程 x(单位:百公里)的函数图象分别如图所示,已知甲车每百公里平均耗油量比乙车每百公里平均耗油量少 2 L,则下列关系正确的是(
A.$\frac{16}{m}-\frac{20}{m}= 2$
B.$\frac{20}{m}-\frac{16}{m}= 2$
C.$\frac{m}{16}-\frac{m}{20}= 2$
D.$\frac{m}{20}-\frac{m}{16}= 2$
B
).
A.$\frac{16}{m}-\frac{20}{m}= 2$
B.$\frac{20}{m}-\frac{16}{m}= 2$
C.$\frac{m}{16}-\frac{m}{20}= 2$
D.$\frac{m}{20}-\frac{m}{16}= 2$
答案:B [解析]由图象知,甲、乙两车行驶m百公里时,甲车耗油40-24=16(L),乙车耗油40-20=20(L),由题意,得20/m-16/m=2. 故选 B.