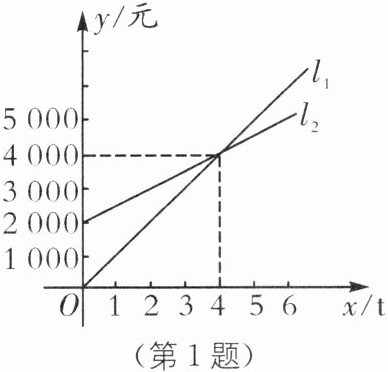
1. 如图,$l_{1}$反映了某公司的销售收入(单位:元)与销售量(单位:t)的关系,$l_{2}$反映了该公司产品的销售成本(单位:元)与销售量(单位:t)的关系,当该公司盈利(收入大于成本)时,销售量应满足的范围是(
A.小于3 t
B.小于4 t
C.大于3 t
D.大于4 t
D
).
A.小于3 t
B.小于4 t
C.大于3 t
D.大于4 t
答案:D
解析:
由图可知,当销售量为$4t$时,销售收入与销售成本相等。当销售量大于$4t$时,$l_{1}$在$l_{2}$上方,即收入大于成本。
D
D
2. 商场有成本为8元的钢笔若干支,据统计钢笔的销售金额y(元)与销售量x(支)的函数关系图象如图所示,则降价后每支钢笔的利润率为(

A.25%
B.33.3%
C.37.5%
D.50%
A
).
A.25%
B.33.3%
C.37.5%
D.50%
答案:A [解析]降价后每支钢笔的价格为(1000-600)÷(80-40)=10(元),降价后每支钢笔的利润率为(10-8)÷8×100%=25%.故选A.
3. 实验班原创 如图(1),在长方形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,$\triangle MNR$的面积为y,若y关于x的函数图象如图(2)所示,则下列说法不正确的是(

A.当$x= 2$时,$y= 5$
B.长方形MNPQ的面积是20
C.当$x= 6$时,$y= 10$
D.当$y= \frac{15}{2}$时,$x= 10$
D
).
A.当$x= 2$时,$y= 5$
B.长方形MNPQ的面积是20
C.当$x= 6$时,$y= 10$
D.当$y= \frac{15}{2}$时,$x= 10$
答案:D [解析]由题图
(2)可知PN=MQ=4,PQ=MN=5.
A. 当x=2时,y= $\frac{1}{2}$×MN×RN= $\frac{1}{2}$×5×2=5,故A正确,与要求不符;B. 长方形MNPQ的面积=MN·PN=5×4=20,故B正确,与要求不符;C. 当x=6时,点R在QP上,y= $\frac{1}{2}$×MN×PN=10,故C正确,与要求不符;D. 当y= $\frac{15}{2}$时,x=3或x=10,故D错误,与要求相符.故选D.
(2)可知PN=MQ=4,PQ=MN=5.
A. 当x=2时,y= $\frac{1}{2}$×MN×RN= $\frac{1}{2}$×5×2=5,故A正确,与要求不符;B. 长方形MNPQ的面积=MN·PN=5×4=20,故B正确,与要求不符;C. 当x=6时,点R在QP上,y= $\frac{1}{2}$×MN×PN=10,故C正确,与要求不符;D. 当y= $\frac{15}{2}$时,x=3或x=10,故D错误,与要求相符.故选D.
4. (湖北武汉华中师大附中自主招生)如图(1),点G是BC上靠近点C的三等分点,点H在AF上,动点P以每秒1 cm的速度沿图(1)的边线运动,运动路径为G-C-D-E-F-H,相应的$\triangle ABP的面积y(cm^{2})关于运动时间t(s)$的函数图象如图(2),若$AB= 4\ cm$,则下列四个结论中正确的有(
A.1个
B.2个
C.3个
D.4个
D
).A.1个
B.2个
C.3个
D.4个
答案:D [解析]根据函数图象可知,当点P在G点时,y= $\frac{1}{2}$AB·BG=12.
∵AB=4cm,
∴BG=6cm.
又从0到3s,y随t的增大而增大,
∴经过了3s,点P运动了3cm,
∴CG=3cm,
∴BC=BG+CG=6+3=9(cm).故①正确;
当t=6时,点P在点D处,
∴y= $\frac{1}{2}$AB·BC= $\frac{1}{2}$×4×9=18,
∴题图
(2)中的M点表示第6s时y的值为18cm².故②正确;
当点P从点C运动到点D时,△ABP的面积不变,
由题图
(2)知,点P从点C运动到点D需要3s,
∴CD=3×1=3(cm).故③正确;
由题图
(2)知,当6≤t≤11时,点P在DE上运动,
∴DE=1×5=5(cm),
∴AF=BC+DE=9+5=14(cm).
∵FH=(19-12)×1=7(cm),
∴AH=AF-FH=14-7=7(cm),
∴题图
(2)中的N点表示第19s时,点P到达H点,
∴△ABP的面积y= $\frac{1}{2}$AB·AH= $\frac{1}{2}$×4×7=14(cm²).
故④正确.故选D.
∵AB=4cm,
∴BG=6cm.
又从0到3s,y随t的增大而增大,
∴经过了3s,点P运动了3cm,
∴CG=3cm,
∴BC=BG+CG=6+3=9(cm).故①正确;
当t=6时,点P在点D处,
∴y= $\frac{1}{2}$AB·BC= $\frac{1}{2}$×4×9=18,
∴题图
(2)中的M点表示第6s时y的值为18cm².故②正确;
当点P从点C运动到点D时,△ABP的面积不变,
由题图
(2)知,点P从点C运动到点D需要3s,
∴CD=3×1=3(cm).故③正确;
由题图
(2)知,当6≤t≤11时,点P在DE上运动,
∴DE=1×5=5(cm),
∴AF=BC+DE=9+5=14(cm).
∵FH=(19-12)×1=7(cm),
∴AH=AF-FH=14-7=7(cm),
∴题图
(2)中的N点表示第19s时,点P到达H点,
∴△ABP的面积y= $\frac{1}{2}$AB·AH= $\frac{1}{2}$×4×7=14(cm²).
故④正确.故选D.
5. (湖南衡阳自主招生)甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度$y(m)与挖掘时间x(h)$之间的关系如图所示,根据图象所提供的信息,其中不正确的是(

A.甲队挖掘30 m时,用了3 h
B.挖掘5 h时甲队比乙队多挖了5 m
C.乙队的挖掘速度总是小于甲队
D.开挖后甲、乙两队所挖河渠长度相等时,$x= 4$
C
).
A.甲队挖掘30 m时,用了3 h
B.挖掘5 h时甲队比乙队多挖了5 m
C.乙队的挖掘速度总是小于甲队
D.开挖后甲、乙两队所挖河渠长度相等时,$x= 4$
答案:C [解析]由图象,得甲队的速度为60÷6=10(m/h),故甲队挖掘30m,用时30÷10=3(h),故A正确;当x>2时,乙队的速度为(50-30)÷(6-2)=5(m/h),故挖掘5h时甲队比乙队多挖了10×5-[30+(5-2)×5]=5(m),故B正确;前2h乙队挖得快,在2~6h之间,甲队挖得快,故C错误;当2<x<6时,令[30+5(x-2)]-10x=0,得x=4,故D正确.故选C.