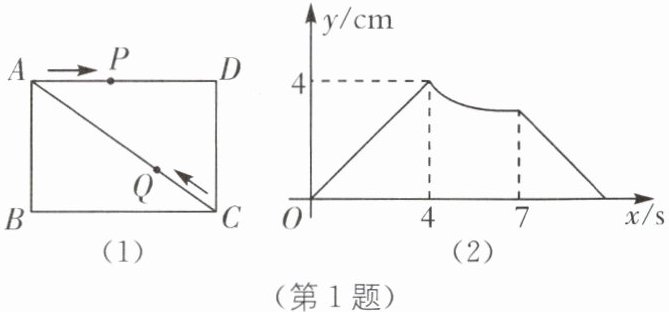
1.(河南自主招生)如图(1),在长方形ABCD中,动点P从点A出发沿A→D→C方向运动到点C停止,动点Q从点C出发沿C→A方向运动到点A停止,若点P,Q同时出发,点P的速度为2 cm/s,点Q的速度为1 cm/s,设运动时间为x s,AP - CQ = y cm,y与x的函数关系图象如图(2)所示,则AC的长为(
A.8 cm
B.9 cm
C.10 cm
D.14 cm
C
).
A.8 cm
B.9 cm
C.10 cm
D.14 cm
答案:C [解析]根据题意,结合函数图象可知,当0≤x<4时,点P在AD上运动;当x=4时,点P运动到点D,即AD=2×4=8(cm);当4<x<7时,点P在DC上运动;当x=7时,点P运动到点C,即CD=2×7 - 8=6(cm).在Rt△ADC中,AD=8cm,CD=6cm,则AC=10cm.故选C.
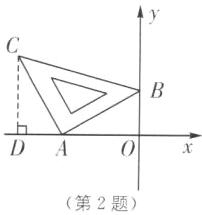
2.如图,将含45°角的直角三角尺放置在平面直角坐标系中,其中点A(-2,0),B(0,1),则直线BC的函数表达式为______.


答案:
y=−$\frac{1}{3}$x + 1 [解析]如图,过点C作CD⊥x轴于点D.
∵∠CAB=90°,
∴∠DAC + ∠BAO = ∠BAO + ∠ABO = 90°,
∴∠DAC = ∠ABO.
在△AOB和△CDA中,$\begin{cases}∠AOB = ∠CDA\\∠ABO = ∠CAD\\AB = CA\end{cases}$
∴△AOB≌△CDA(AAS).
∵A(−2,0),B(0,1),
∴AD = BO = 1,CD = AO = 2,
∴OD = OA + AD = 3,
∴C(−3,2).
设直线BC的函数表达式为y = kx + b,
∴$\begin{cases}-3k + b = 2\\b = 1\end{cases}$解得$\begin{cases}k = -\frac{1}{3}\\b = 1\end{cases}$
∴直线BC的函数表达式为y = −$\frac{1}{3}$x + 1.
归纳总结:本题主要考查待定系数法及全等三角形的判定和性质,构造全等三角形求得点C的坐标是解题的关键.
y=−$\frac{1}{3}$x + 1 [解析]如图,过点C作CD⊥x轴于点D.
∵∠CAB=90°,
∴∠DAC + ∠BAO = ∠BAO + ∠ABO = 90°,
∴∠DAC = ∠ABO.
在△AOB和△CDA中,$\begin{cases}∠AOB = ∠CDA\\∠ABO = ∠CAD\\AB = CA\end{cases}$
∴△AOB≌△CDA(AAS).
∵A(−2,0),B(0,1),
∴AD = BO = 1,CD = AO = 2,
∴OD = OA + AD = 3,
∴C(−3,2).
设直线BC的函数表达式为y = kx + b,
∴$\begin{cases}-3k + b = 2\\b = 1\end{cases}$解得$\begin{cases}k = -\frac{1}{3}\\b = 1\end{cases}$
∴直线BC的函数表达式为y = −$\frac{1}{3}$x + 1.
归纳总结:本题主要考查待定系数法及全等三角形的判定和性质,构造全等三角形求得点C的坐标是解题的关键.

3.如图,正方形ABCD的边长为4,动点E从点A出发,以每秒2个单位的速度沿A→D→A运动,动点G从点A出发,以每秒1个单位的速度沿A→B运动,当有一个点到达终点时,另一点随之也停止运动.过点G作FG⊥AB交AC于点F.设运动时间为t(单位:秒).以FG为一直角边向右作等腰直角三角形FGH,△FGH与正方形ABCD重叠部分的面积为S.

(1)当t = 1.5时,S = ______;当t = 3时,S = ______.
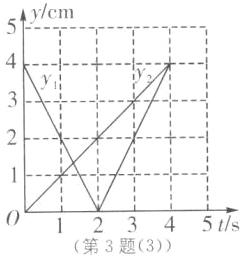
(2)在如图所示的网格坐标系中,设$DE = y_1,AG = y_2,$画出$y_1$与$y_2$关于t的函数图象.

(1)当t = 1.5时,S = ______;当t = 3时,S = ______.
(2)在如图所示的网格坐标系中,设$DE = y_1,AG = y_2,$画出$y_1$与$y_2$关于t的函数图象.
答案:
(1)$\frac{9}{8}$ $\frac{5}{2}$ [解析]
∵四边形ABCD是边长为4的正方形,
∴AB = AD = 4,∠CAB = 45°.
∵△FGH是等腰直角三角形,
∴∠FGH = 90°,FG = GH,∠GFH = ∠GHF = 45°,则AG = FG = GH = t.当t = 1.5时,如图
(1),重叠部分面积S = S△FGH = $\frac{1}{2}$FG·GH = $\frac{9}{8}$;

当t = 3时,如图
(2),
∵AG = FG = GH = 3,AB = 4,
∴GB = AB - AG = 1,BH = GH - GB = 2.
∵∠PBH = 90°,∠H = 45°,
∴BH = BP = 2,
则重叠部分面积S = S梯形PBGF = $\frac{1}{2}$(PB + FG)·GB = $\frac{1}{2}$×(2 + 3)×1 = $\frac{5}{2}$.
(2)由题意知,点E的运动路程为2t,
如图
(1),点E从A到D,即0≤t≤2时,DE = AD - AE = 4 - 2t,即y1 = 4 - 2t;
如图
(2),点E从点D返回点A,即2<t≤4时,DE = 2t - 4,即y1 = 2t - 4,
∴y1 = $\begin{cases}4 - 2t(0≤t≤2)\\2t - 4(2<t≤4)\end{cases}$;y2 = t(0≤t≤4).
∴y1,y2关于t的函数图象如图
(3)所示:
(1)$\frac{9}{8}$ $\frac{5}{2}$ [解析]
∵四边形ABCD是边长为4的正方形,
∴AB = AD = 4,∠CAB = 45°.
∵△FGH是等腰直角三角形,
∴∠FGH = 90°,FG = GH,∠GFH = ∠GHF = 45°,则AG = FG = GH = t.当t = 1.5时,如图
(1),重叠部分面积S = S△FGH = $\frac{1}{2}$FG·GH = $\frac{9}{8}$;

当t = 3时,如图
(2),
∵AG = FG = GH = 3,AB = 4,
∴GB = AB - AG = 1,BH = GH - GB = 2.
∵∠PBH = 90°,∠H = 45°,
∴BH = BP = 2,
则重叠部分面积S = S梯形PBGF = $\frac{1}{2}$(PB + FG)·GB = $\frac{1}{2}$×(2 + 3)×1 = $\frac{5}{2}$.
(2)由题意知,点E的运动路程为2t,
如图
(1),点E从A到D,即0≤t≤2时,DE = AD - AE = 4 - 2t,即y1 = 4 - 2t;
如图
(2),点E从点D返回点A,即2<t≤4时,DE = 2t - 4,即y1 = 2t - 4,
∴y1 = $\begin{cases}4 - 2t(0≤t≤2)\\2t - 4(2<t≤4)\end{cases}$;y2 = t(0≤t≤4).
∴y1,y2关于t的函数图象如图
(3)所示:

4.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB = 90°,BC = 10,点A,B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y = x - 5上时,线段BC扫过的面积为(
A.80
B.88
C.96
D.100
B
).A.80
B.88
C.96
D.100
答案:B [解析]
∵点A,B的坐标分别为(2,0),(8,0),
∴AB = 6.
∵∠CAB = 90°,BC = 10,
∴CA = 8.
∴点C的纵坐标为8.
∵将△ABC沿x轴向右平移,当点C落在直线y = x - 5上时,将y = 8代入,解得x = 13,即点C向右平移了13 - 2 = 11(个)单位长度,
∴线段BC扫过的面积为11×8 = 88.故选B.
∵点A,B的坐标分别为(2,0),(8,0),
∴AB = 6.
∵∠CAB = 90°,BC = 10,
∴CA = 8.
∴点C的纵坐标为8.
∵将△ABC沿x轴向右平移,当点C落在直线y = x - 5上时,将y = 8代入,解得x = 13,即点C向右平移了13 - 2 = 11(个)单位长度,
∴线段BC扫过的面积为11×8 = 88.故选B.
5.数形结合思想 如图,在平面直角坐标系中,直线AB与x轴交于点A(8,0),与y轴交于点B(0,8),点D为OA延长线上一动点,以BD为直角边在其上方作等腰直角三角形BDE,连接EA.
(1)求证:∠EAD = ∠OAB;
(2)求直线EA与y轴交点F的坐标.

(1)求证:∠EAD = ∠OAB;
(2)求直线EA与y轴交点F的坐标.

答案:
(1)如图
(1),过点E作EG⊥x轴于点G.
∵△BDE是等腰直角三角形,
∴∠EGD = ∠DOB = ∠EDB = 90°,ED = DB,
∴∠1 + ∠2 = 90°,∠2 + ∠3 = 90°,
∴∠1 = ∠3.
在△EGD和△DOB中,$\begin{cases}∠EGD = ∠DOB\\∠1 = ∠3\\ED = DB\end{cases}$
∴△EGD≌△DOB(AAS),
∴EG = DO,GD = OB.
∵A(8,0),B(0,8),
∴OB = OA = 8,
∴∠OAB = 45°,GD = OA,
∴DO = DA + OA = DA + DG = AG,
∴EG = AG,
∴∠EAG = ∠GEA = 45°,
∴∠EAD = ∠OAB.

(2)如图
(2),延长EA交y轴于点F.
∵∠EAD = 45°,
∴∠OAF = 45°,
∴OA = OF = 8,
∴点F的坐标为(0,−8).
归纳总结:本题是一次函数综合题,主要考查了一次函数的性质、全等三角形的判定和性质、等腰直角三角形的性质,解本题的关键是作辅助线构造全等三角形.
(1)如图
(1),过点E作EG⊥x轴于点G.
∵△BDE是等腰直角三角形,
∴∠EGD = ∠DOB = ∠EDB = 90°,ED = DB,
∴∠1 + ∠2 = 90°,∠2 + ∠3 = 90°,
∴∠1 = ∠3.
在△EGD和△DOB中,$\begin{cases}∠EGD = ∠DOB\\∠1 = ∠3\\ED = DB\end{cases}$
∴△EGD≌△DOB(AAS),
∴EG = DO,GD = OB.
∵A(8,0),B(0,8),
∴OB = OA = 8,
∴∠OAB = 45°,GD = OA,
∴DO = DA + OA = DA + DG = AG,
∴EG = AG,
∴∠EAG = ∠GEA = 45°,
∴∠EAD = ∠OAB.

(2)如图
(2),延长EA交y轴于点F.
∵∠EAD = 45°,
∴∠OAF = 45°,
∴OA = OF = 8,
∴点F的坐标为(0,−8).
归纳总结:本题是一次函数综合题,主要考查了一次函数的性质、全等三角形的判定和性质、等腰直角三角形的性质,解本题的关键是作辅助线构造全等三角形.