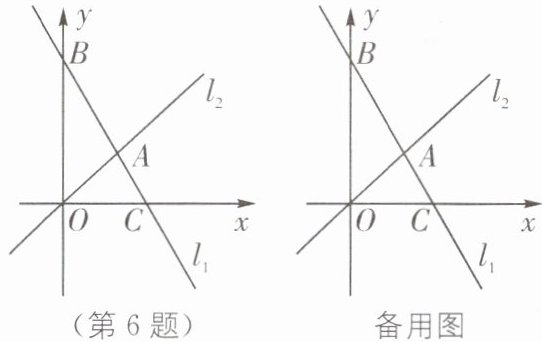
6.如图,在平面直角坐标系中,直线$l_1:y = kx + b(k ≠ 0)与直线l_2:y = x$交于点A(2,a),与y轴交于点B(0,6),与x轴交于点C.
(1)求直线$l_1$的函数表达式;
(2)在平面直角坐标系中有一点P(5,m),使得$S_{△AOP} = S_{△AOC}$,请求出点P的坐标;
(3)点M为直线$l_1$上的动点,过点M作y轴的平行线,交$l_2$于点N,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点M的坐标.
(1)求直线$l_1$的函数表达式;
(2)在平面直角坐标系中有一点P(5,m),使得$S_{△AOP} = S_{△AOC}$,请求出点P的坐标;
(3)点M为直线$l_1$上的动点,过点M作y轴的平行线,交$l_2$于点N,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点M的坐标.

答案:
(1)
∵点A(2,a)在直线l2:y = x上,
∴a = 2,即A(2,2).
∵直线l1:y = kx + b(k≠0)过点A(2,2),点B(0,6),
∴$\begin{cases}2k + b = 2\\b = 6\end{cases}$解得$\begin{cases}k = -2\\b = 6\end{cases}$
∴直线l1的函数表达式为y = −2x + 6.
(2)
∵S△AOP = S△AOC,
∴当以AO为底边时,两三角形等高,
∴设过点P且与直线AO平行的直线l3为y = x + d.
y = 0时,0 = −2x + 6,
∴点C坐标为(3,0).
①当直线l3过点C(3,0)时,得l3为y = x - 3,
当x = 5时,m = 5 - 3 = 2,
∴点P的坐标为(5,2);
②点C(3,0)关于直线OA的对称点为(0,3),
当直线l3过点(0,3)时,得l3为y = x + 3,
当x = 5时,m = 5 + 3 = 8,
∴点P的坐标为(5,8).
综上所述,点P的坐标为(5,2)或(5,8).
(3)设M(t,−2t + 6),则N(t,t),
∴MN = |−2t + 6 - t| = |3t - 6|,
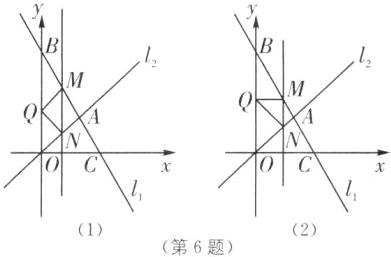
①如图
(1),若∠MQN = 90°,MQ = NQ,
则MN = 2|xM| = 2|t|,
∴|3t - 6| = 2|t|,
∴t = $\frac{6}{5}$或t = 6,
∴M($\frac{6}{5}$,$\frac{18}{5}$)或(6,−6);
②如图
(2),若∠QMN = 90°或∠QNM = 90°(此种情况图略),则MN = |xM| = |t|,
∴|3t - 6| = |t|,
∴t = $\frac{3}{2}$或t = 3,
∴M($\frac{3}{2}$,3)或(3,0).
综上所述,点M的坐标为($\frac{6}{5}$,$\frac{18}{5}$)或(6,−6)或($\frac{3}{2}$,3)或(3,0).
(1)
∵点A(2,a)在直线l2:y = x上,
∴a = 2,即A(2,2).
∵直线l1:y = kx + b(k≠0)过点A(2,2),点B(0,6),
∴$\begin{cases}2k + b = 2\\b = 6\end{cases}$解得$\begin{cases}k = -2\\b = 6\end{cases}$
∴直线l1的函数表达式为y = −2x + 6.
(2)
∵S△AOP = S△AOC,
∴当以AO为底边时,两三角形等高,
∴设过点P且与直线AO平行的直线l3为y = x + d.
y = 0时,0 = −2x + 6,
∴点C坐标为(3,0).
①当直线l3过点C(3,0)时,得l3为y = x - 3,
当x = 5时,m = 5 - 3 = 2,
∴点P的坐标为(5,2);
②点C(3,0)关于直线OA的对称点为(0,3),
当直线l3过点(0,3)时,得l3为y = x + 3,
当x = 5时,m = 5 + 3 = 8,
∴点P的坐标为(5,8).
综上所述,点P的坐标为(5,2)或(5,8).
(3)设M(t,−2t + 6),则N(t,t),
∴MN = |−2t + 6 - t| = |3t - 6|,
①如图
(1),若∠MQN = 90°,MQ = NQ,
则MN = 2|xM| = 2|t|,
∴|3t - 6| = 2|t|,
∴t = $\frac{6}{5}$或t = 6,
∴M($\frac{6}{5}$,$\frac{18}{5}$)或(6,−6);
②如图
(2),若∠QMN = 90°或∠QNM = 90°(此种情况图略),则MN = |xM| = |t|,
∴|3t - 6| = |t|,
∴t = $\frac{3}{2}$或t = 3,
∴M($\frac{3}{2}$,3)或(3,0).
综上所述,点M的坐标为($\frac{6}{5}$,$\frac{18}{5}$)或(6,−6)或($\frac{3}{2}$,3)或(3,0).

7.如图,在平面直角坐标系xOy中,直线$y = -\frac{4}{3}x + 4$与x轴、y轴分别交于点A,B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴的正半轴上的点C处.
(1)求AB的长.
(2)求点C和点D的坐标.
(3)在y轴上是否存在一点P,使得$S_{△PAB} = \frac{1}{2}S_{△OCD}$?若存在,直接写出点P的坐标;若不存在,请说明理由.

(1)求AB的长.
(2)求点C和点D的坐标.
(3)在y轴上是否存在一点P,使得$S_{△PAB} = \frac{1}{2}S_{△OCD}$?若存在,直接写出点P的坐标;若不存在,请说明理由.

答案:
(1)在y = −$\frac{4}{3}$x + 4中,令x = 0,得y = 4,
∴B(0,4),即OB = 4.
令y = 0,得0 = −$\frac{4}{3}$x + 4,解得x = 3,
∴A(3,0),即OA = 3.
在Rt△OAB中,AB = $\sqrt{OA^{2}+OB^{2}}$ = 5.
(2)由
(1)知,AB = 5,则由折叠可知,AC = AB = 5,
∴OC = OA + AC = 3 + 5 = 8,
∴C(8,0).
设OD = m,则CD = DB = m + 4.
在Rt△OCD中,DC² = OD² + OC²,
即(m + 4)² = m² + 8²,解得m = 6,
∴D(0,−6).
(3)存在,点P坐标为(0,12)或(0,−4).理由如下:
∵S△PAB = $\frac{1}{2}$S△OCD,
∴S△PAB = $\frac{1}{2}$×$\frac{1}{2}$×6×8 = 12.
∵点P在y轴上,
∴$\frac{1}{2}$BP·OA = 12,
即$\frac{1}{2}$×3BP = 12,解得BP = 8.
∴点P的坐标为(0,12)或(0,−4).
(1)在y = −$\frac{4}{3}$x + 4中,令x = 0,得y = 4,
∴B(0,4),即OB = 4.
令y = 0,得0 = −$\frac{4}{3}$x + 4,解得x = 3,
∴A(3,0),即OA = 3.
在Rt△OAB中,AB = $\sqrt{OA^{2}+OB^{2}}$ = 5.
(2)由
(1)知,AB = 5,则由折叠可知,AC = AB = 5,
∴OC = OA + AC = 3 + 5 = 8,
∴C(8,0).
设OD = m,则CD = DB = m + 4.
在Rt△OCD中,DC² = OD² + OC²,
即(m + 4)² = m² + 8²,解得m = 6,
∴D(0,−6).
(3)存在,点P坐标为(0,12)或(0,−4).理由如下:
∵S△PAB = $\frac{1}{2}$S△OCD,
∴S△PAB = $\frac{1}{2}$×$\frac{1}{2}$×6×8 = 12.
∵点P在y轴上,
∴$\frac{1}{2}$BP·OA = 12,
即$\frac{1}{2}$×3BP = 12,解得BP = 8.
∴点P的坐标为(0,12)或(0,−4).
8.如图,直线$l_1的表达式为y = \frac{4}{3}x + 4$,与x轴、y轴分别交于点A,B;直线$l_2$与x轴交于点C(2,0),与y轴交于点$D(0,\frac{3}{2})$,两直线交于点$P(-\frac{6}{5},\frac{12}{5})$.
(1)求点A,B的坐标及直线$l_2$的函数表达式;
(2)求证:△AOB≌△APC;
(3)若将直线$l_2$向右平移m个单位,与x轴、y轴分别交于点$C',D'$,使得以点A,B,C',D'为顶点的图形是轴对称图形,求m的值.

(1)求点A,B的坐标及直线$l_2$的函数表达式;
(2)求证:△AOB≌△APC;
(3)若将直线$l_2$向右平移m个单位,与x轴、y轴分别交于点$C',D'$,使得以点A,B,C',D'为顶点的图形是轴对称图形,求m的值.

答案:
(1)当x = 0时,y = $\frac{4}{3}$x + 4 = 4,
∴点B的坐标为(0,4).
当y = 0时,有$\frac{4}{3}$x + 4 = 0,解得x = −3,
∴点A的坐标为(−3,0).
设直线l2的表达式为y = kx + b(k≠0),
将C(2,0),D(0,$\frac{3}{2}$)代入y = kx + b,
得$\begin{cases}2k + b = 0\\b = \frac{3}{2}\end{cases}$解得$\begin{cases}k = -\frac{3}{4}\\b = \frac{3}{2}\end{cases}$
∴直线l2的表达式为y = −$\frac{3}{4}$x + $\frac{3}{2}$.
(2)
∵A(−3,0),C(2,0),B(0,4),P(−$\frac{6}{5}$,$\frac{12}{5}$),
∴AO = 3,AC = 5,AB = $\sqrt{3^{2}+4^{2}}$ = 5,
AP = $\sqrt{[-\frac{6}{5}-(-3)]^{2}+(\frac{12}{5}-0)^{2}}$ = 3,
∴AO = AP,AB = AC.
在△AOB和△APC中,$\begin{cases}AO = AP\\∠BAO = ∠CAP\\AB = AC\end{cases}$
∴△AOB≌△APC(SAS).
(3)①如图
(1),当点B在点D'下方时,连接BC'.
∵平移后直线C'D'的表达式为y = −$\frac{3}{4}$(x - m) + $\frac{3}{2}$ = −$\frac{3}{4}$x + $\frac{3}{4}$m + $\frac{3}{2}$,
∴点C'的坐标为(m + 2,0),点D'的坐标为(0,$\frac{3}{4}$m + $\frac{3}{2}$).
由题意,可得以点A,B,C',D'为顶点的图形是轴对称图形,当△ABC'≌△D'BC'时,有AB = D'B,AC' = D'C'.
∵A(−3,0),B(0,4),
∴D'B = $\frac{3}{4}$m + $\frac{3}{2}$ - 4 = $\frac{3}{4}$m - $\frac{5}{2}$,
AC' = m + 2 - (-3) = m + 5,
D'C' = $\sqrt{(m + 2)^{2}+(\frac{3}{4}m + \frac{3}{2})^{2}}$ = $\frac{5}{4}$(m + 2).
∴$\begin{cases}\frac{3}{4}m - \frac{5}{2} = 5\\m + 5 = \frac{5}{4}(m + 2)\end{cases}$解得m = 10.

②如图
(2),当点B在点D'上方时,连接BC',AD'.
若△AC'D'≌△BC'D',则AC' = BC',
由①可得BC' = $\sqrt{(m + 2)^{2}+4^{2}}$,AC' = m + 5,
∴m + 5 = $\sqrt{(m + 2)^{2}+4^{2}}$,
解得m = −$\frac{5}{6}$(不合题意,舍去);
若△ABD'≌△C'BD',则AB = C'B,
∴OA = OC',即3 = m + 2,解得m = 1.
故以点A,B,C',D'为顶点的图形是轴对称图形时,m的值为10或1.
(1)当x = 0时,y = $\frac{4}{3}$x + 4 = 4,
∴点B的坐标为(0,4).
当y = 0时,有$\frac{4}{3}$x + 4 = 0,解得x = −3,
∴点A的坐标为(−3,0).
设直线l2的表达式为y = kx + b(k≠0),
将C(2,0),D(0,$\frac{3}{2}$)代入y = kx + b,
得$\begin{cases}2k + b = 0\\b = \frac{3}{2}\end{cases}$解得$\begin{cases}k = -\frac{3}{4}\\b = \frac{3}{2}\end{cases}$
∴直线l2的表达式为y = −$\frac{3}{4}$x + $\frac{3}{2}$.
(2)
∵A(−3,0),C(2,0),B(0,4),P(−$\frac{6}{5}$,$\frac{12}{5}$),
∴AO = 3,AC = 5,AB = $\sqrt{3^{2}+4^{2}}$ = 5,
AP = $\sqrt{[-\frac{6}{5}-(-3)]^{2}+(\frac{12}{5}-0)^{2}}$ = 3,
∴AO = AP,AB = AC.
在△AOB和△APC中,$\begin{cases}AO = AP\\∠BAO = ∠CAP\\AB = AC\end{cases}$
∴△AOB≌△APC(SAS).
(3)①如图
(1),当点B在点D'下方时,连接BC'.
∵平移后直线C'D'的表达式为y = −$\frac{3}{4}$(x - m) + $\frac{3}{2}$ = −$\frac{3}{4}$x + $\frac{3}{4}$m + $\frac{3}{2}$,
∴点C'的坐标为(m + 2,0),点D'的坐标为(0,$\frac{3}{4}$m + $\frac{3}{2}$).
由题意,可得以点A,B,C',D'为顶点的图形是轴对称图形,当△ABC'≌△D'BC'时,有AB = D'B,AC' = D'C'.
∵A(−3,0),B(0,4),
∴D'B = $\frac{3}{4}$m + $\frac{3}{2}$ - 4 = $\frac{3}{4}$m - $\frac{5}{2}$,
AC' = m + 2 - (-3) = m + 5,
D'C' = $\sqrt{(m + 2)^{2}+(\frac{3}{4}m + \frac{3}{2})^{2}}$ = $\frac{5}{4}$(m + 2).
∴$\begin{cases}\frac{3}{4}m - \frac{5}{2} = 5\\m + 5 = \frac{5}{4}(m + 2)\end{cases}$解得m = 10.

②如图
(2),当点B在点D'上方时,连接BC',AD'.
若△AC'D'≌△BC'D',则AC' = BC',
由①可得BC' = $\sqrt{(m + 2)^{2}+4^{2}}$,AC' = m + 5,
∴m + 5 = $\sqrt{(m + 2)^{2}+4^{2}}$,
解得m = −$\frac{5}{6}$(不合题意,舍去);
若△ABD'≌△C'BD',则AB = C'B,
∴OA = OC',即3 = m + 2,解得m = 1.
故以点A,B,C',D'为顶点的图形是轴对称图形时,m的值为10或1.