6. (2024·济南中考)某公司生产了 A,B 两款新能源电动汽车. 如图,$ l_1 $,$ l_2 $ 分别表示 A 款,B 款新能源电动汽车充满电后电池的剩余电量 $ y $(kW·h)与汽车行驶路程 $ x $(km)的关系. 当两款新能源电动汽车的行驶路程都是 300 km 时,A 款新能源电动汽车电池的剩余电量比 B 款新能源电动汽车电池的剩余电量多
12
kW·h.答案:12 解析 A款新能源电动汽车每千米的耗电量为(80-48)÷200=0.16(kW·h),B款新能源电动汽车每千米的耗电量为(80-40)÷200=0.2(kW·h),
∴l₁图象的函数关系式为y₁=80-0.16x,l₂图象的函数关系式为y₂=80-0.2x,
当x=300时,y₁=80-0.16×300=32,y₂=80-0.2×300=20,32-20=12(kW·h),
∴当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多12kW·h.
∴l₁图象的函数关系式为y₁=80-0.16x,l₂图象的函数关系式为y₂=80-0.2x,
当x=300时,y₁=80-0.16×300=32,y₂=80-0.2×300=20,32-20=12(kW·h),
∴当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多12kW·h.
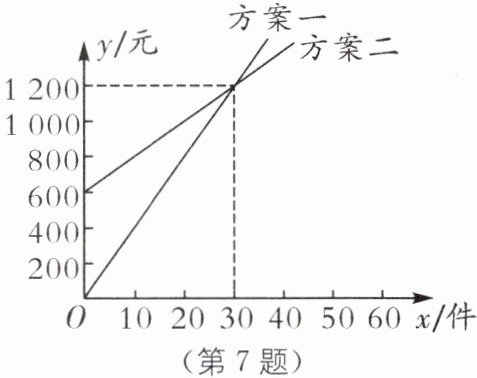
7. 新情境 选择方案 (2023·丽水中考)我市“共富工坊”问海借力,某公司产品销售量得到大幅提升. 为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同. 看图解答下列问题:
(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2)求方案二 $ y $ 关于 $ x $ 的函数表达式;
(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.
(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2)求方案二 $ y $ 关于 $ x $ 的函数表达式;
(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.

答案:
(1)观察图象,得方案一与方案二相交于点(30,1200),
∴员工生产30件产品时,两种方案付给的报酬一样多.
(2)设方案二的函数表达式为y=kx+b,
将点(0,600),点(30,1200)代入表达式,
得{30k+b=1200, b=600,解得{k=20, b=600.
故方案二y关于x的函数表达式为y=20x+600.
(3)由两方案的图象交点(30,1200)可知,
若生产件数x的取值范围为0≤x<30,则选择方案二;
若生产件数x=30,则选择两个方案都可以;
若生产件数x的取值范围为x>30,则选择方案一.
归纳总结 本题考查的是求解一次函数表达式以及一次函数的实际应用,解题关键是会看图,理解横轴与纵轴表示的实际意义,掌握用待定系数法求函数表达式.
(1)观察图象,得方案一与方案二相交于点(30,1200),
∴员工生产30件产品时,两种方案付给的报酬一样多.
(2)设方案二的函数表达式为y=kx+b,
将点(0,600),点(30,1200)代入表达式,
得{30k+b=1200, b=600,解得{k=20, b=600.
故方案二y关于x的函数表达式为y=20x+600.
(3)由两方案的图象交点(30,1200)可知,
若生产件数x的取值范围为0≤x<30,则选择方案二;
若生产件数x=30,则选择两个方案都可以;
若生产件数x的取值范围为x>30,则选择方案一.
归纳总结 本题考查的是求解一次函数表达式以及一次函数的实际应用,解题关键是会看图,理解横轴与纵轴表示的实际意义,掌握用待定系数法求函数表达式.
8. (2023·齐齐哈尔中考)一辆巡逻车从 A 地出发沿一条笔直的公路匀速驶向 B 地,$ \frac{2}{5} $ 小时后,一辆货车从 A 地出发,沿同一路线每小时行驶 80 千米匀速驶向 B 地,货车到达 B 地填装货物耗时 15 分钟,然后立即按原路匀速返回 A 地. 巡逻车、货车离 A 地的距离 $ y $(千米)与货车出发时间 $ x $(小时)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A,B 两地之间的距离是______千米,$ a= $______.
(2)求线段 FG 所在直线的函数表达式.
(3)货车出发多少小时两车相距 15 千米?(直接写出答案即可)

(1)A,B 两地之间的距离是
(2)求线段 FG 所在直线的函数表达式.
(3)货车出发多少小时两车相距 15 千米?(直接写出答案即可)
(1)A,B 两地之间的距离是______千米,$ a= $______.
(2)求线段 FG 所在直线的函数表达式.
(3)货车出发多少小时两车相距 15 千米?(直接写出答案即可)

(1)A,B 两地之间的距离是
60
千米,$ a= $1
.(2)求线段 FG 所在直线的函数表达式.
设线段FG所在直线的表达式为y=kx+b(k≠0).将F(1,60),G(2,0)代入,得{k+b=60, 2k+b=0,解得{k=-60, b=120,∴线段FG所在直线的函数表达式为y=-60x+120.
(3)货车出发多少小时两车相距 15 千米?(直接写出答案即可)
货车出发5/11小时或19/17小时或25/17小时,两车相距15千米.
答案:
(1)60 1 解析
∵80×3/4=60(千米),
∴A,B两地之间的距离是60千米.
∵货车到达B地填装货物耗时15分钟,
∴a=3/4+15/60=1.
(2)设线段FG所在直线的表达式为y=kx+b(k≠0).
将F(1,60),G(2,0)代入,
得{k+b=60, 2k+b=0,解得{k=-60, b=120,
∴线段FG所在直线的函数表达式为y=-60x+120.
(3)巡逻车速度为60÷(2+2/5)=25(千米/时),
∴线段CD的表达式为y=25x+25×2/5=25x+10(0≤x≤2).
当货车第一次追上巡逻车后,80x-(25x+10)=15,
解得x=5/11;
当货车返回与巡逻车未相遇时,(-60x+120)-(25x+10)=15,解得x=19/17;
当货车返回与巡逻车相遇后,(25x+10)-(-60x+120)=15,解得x=25/17.
综上所述,货车出发5/11小时或19/17小时或25/17小时,两车相距15千米.
(1)60 1 解析
∵80×3/4=60(千米),
∴A,B两地之间的距离是60千米.
∵货车到达B地填装货物耗时15分钟,
∴a=3/4+15/60=1.
(2)设线段FG所在直线的表达式为y=kx+b(k≠0).
将F(1,60),G(2,0)代入,
得{k+b=60, 2k+b=0,解得{k=-60, b=120,
∴线段FG所在直线的函数表达式为y=-60x+120.
(3)巡逻车速度为60÷(2+2/5)=25(千米/时),
∴线段CD的表达式为y=25x+25×2/5=25x+10(0≤x≤2).
当货车第一次追上巡逻车后,80x-(25x+10)=15,
解得x=5/11;
当货车返回与巡逻车未相遇时,(-60x+120)-(25x+10)=15,解得x=19/17;
当货车返回与巡逻车相遇后,(25x+10)-(-60x+120)=15,解得x=25/17.
综上所述,货车出发5/11小时或19/17小时或25/17小时,两车相距15千米.