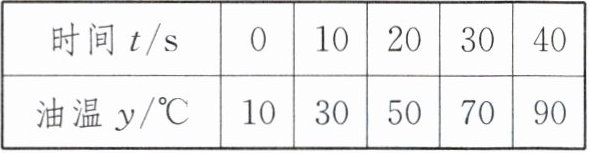
6. 跨学科 测算沸点 (2023·宜昌中考)某食用油的沸点温度远高于水的沸点温度. 小聪想用刻度不超过 100℃的温度计测算出这种食用油沸点的温度. 在老师的指导下,他在锅中倒入一些这种食用油均匀加热,并每隔 10 s 测量一次锅中油温,得到的数据记录如下:
|时间 t/s|0|10|20|30|40|
|油温 y/℃|10|30|50|70|90|
(1)小聪在平面直角坐标系中描出了表中数据对应的点. 经老师介绍,在这种食用油达到沸点前,锅中油温 y(单位:℃)与加热的时间 t(单位:s)符合初中学习过的某种函数关系,填空:可能是______函数关系(请选填“正比例”“一次”“二次”“反比例”);
(2)根据以上判断,求 y 关于 t 的函数表达式;
(3)当加热 110 s 时,油沸腾了,请推算沸点的温度.

(1)
(2)
(3)
|时间 t/s|0|10|20|30|40|
|油温 y/℃|10|30|50|70|90|

(1)小聪在平面直角坐标系中描出了表中数据对应的点. 经老师介绍,在这种食用油达到沸点前,锅中油温 y(单位:℃)与加热的时间 t(单位:s)符合初中学习过的某种函数关系,填空:可能是______函数关系(请选填“正比例”“一次”“二次”“反比例”);
(2)根据以上判断,求 y 关于 t 的函数表达式;
(3)当加热 110 s 时,油沸腾了,请推算沸点的温度.

(1)
一次
(2)
设锅中油温y与加热的时间t的函数表达式为y=kt + b(k≠0),将点(0,10),(10,30)代入,得{b = 10,10k + b = 30,解得{k = 2,b = 10,∴y=2t+10.
(3)
当t=110时,y=2×110+10=230,∴经过推算,该油的沸点温度是230℃.
答案:6.
(1)一次 [解析]根据表格中两个变量对应值变化的规律可知,时间每增加10s,油的温度就升高20℃.故锅中油温y与加热的时间t可能是一次函数关系.
(2)设锅中油温y与加热的时间t的函数表达式为y=kt + b(k≠0),将点(0,10),(10,30)代入,
得{b = 10,10k + b = 30,解得{k = 2,b = 10,
∴y=2t+10.
(3)当t=110时,y=2×110+10=230,
∴经过推算,该油的沸点温度是230℃.
(1)一次 [解析]根据表格中两个变量对应值变化的规律可知,时间每增加10s,油的温度就升高20℃.故锅中油温y与加热的时间t可能是一次函数关系.
(2)设锅中油温y与加热的时间t的函数表达式为y=kt + b(k≠0),将点(0,10),(10,30)代入,
得{b = 10,10k + b = 30,解得{k = 2,b = 10,
∴y=2t+10.
(3)当t=110时,y=2×110+10=230,
∴经过推算,该油的沸点温度是230℃.
7.(2023·襄阳中考)在襄阳市创建“经济品牌特色品牌”政策的影响下. 每到傍晚,市内某网红烧烤店就食客如云,这家烧烤店的海鲜串和肉串非常畅销,店主从食品加工厂批发以上两种产品进行加工销售,其中海鲜串的成本为 m 元/支,肉串的成本为 n 元/支;两次购进并加工海鲜串和肉串的数量与成本如下表所示(成本包括进价和其他费用):
|次数|数量/支| |总成本/元|
| |海鲜串|肉串| |
|第一次|3000|4000|17000|
|第二次|4000|3000|18000|

针对团体消费,店主决定每次消费海鲜串不超过 200 支时,每支售价 5 元;超过 200 支时,不超过 200 支的部分按原价,超过 200 支的部分打 8 折. 每支肉串的售价为 3.5 元.
(1)求 m,n 的值;
(2)五一当天,一个旅游团去此店吃烧烤,一次性消费海鲜串和肉串共 1000 支,且海鲜串不超过 400 支. 在本次消费中,设该旅游团消费海鲜串 x 支,店主获得海鲜串的总利润为 y 元,求 y 与 x 的函数表达式,并写出自变量 x 的取值范围;
(3)在(2)的条件下,该旅游团消费的海鲜串超过了 200 支,店主决定给该旅游团更多优惠,对每支肉串降价 a(0<a<1)元,但要确保本次消费获得肉串的总利润始终不低于海鲜串的总利润,求 a 的最大值.
|次数|数量/支| |总成本/元|
| |海鲜串|肉串| |
|第一次|3000|4000|17000|
|第二次|4000|3000|18000|

针对团体消费,店主决定每次消费海鲜串不超过 200 支时,每支售价 5 元;超过 200 支时,不超过 200 支的部分按原价,超过 200 支的部分打 8 折. 每支肉串的售价为 3.5 元.
(1)求 m,n 的值;
(2)五一当天,一个旅游团去此店吃烧烤,一次性消费海鲜串和肉串共 1000 支,且海鲜串不超过 400 支. 在本次消费中,设该旅游团消费海鲜串 x 支,店主获得海鲜串的总利润为 y 元,求 y 与 x 的函数表达式,并写出自变量 x 的取值范围;
(3)在(2)的条件下,该旅游团消费的海鲜串超过了 200 支,店主决定给该旅游团更多优惠,对每支肉串降价 a(0<a<1)元,但要确保本次消费获得肉串的总利润始终不低于海鲜串的总利润,求 a 的最大值.
答案:7.
(1)根据表格,可得{3000m + 4000n = 17000,4000m + 3000n = 18000,解得{m = 3,n = 2,
∴m的值为3,n的值为2.
(2)当0<x≤200时,店主获得海鲜串的总利润y=(5-3)x=2x;
当200<x≤400时,店主获得海鲜串的总利润y=(5-3)×200+(5×0.8−3)(x−200)=x+200,
∴y = {2x(0 < x ≤ 200),x + 200(200 < x ≤ 400).
(3)设降价后获得肉串的总利润为z元,令W=z−y.
∵200<x≤400,
∴z=(3.5−a−2)(1000−x)=(a−1.5)x+1500−1000a,
∴W=z−y=(a−2.5)x+1300−1000a.
∵0<a<1,
∴a−2.5<0,
∴W随x的增大而减小.
当x=400时,W的值最小.
由题意,可得z≥y,
∴W≥0,
即(a−2.5)×400+1300−1000a≥0,
解得a≤0.5,
∴a的最大值是0.5.
(1)根据表格,可得{3000m + 4000n = 17000,4000m + 3000n = 18000,解得{m = 3,n = 2,
∴m的值为3,n的值为2.
(2)当0<x≤200时,店主获得海鲜串的总利润y=(5-3)x=2x;
当200<x≤400时,店主获得海鲜串的总利润y=(5-3)×200+(5×0.8−3)(x−200)=x+200,
∴y = {2x(0 < x ≤ 200),x + 200(200 < x ≤ 400).
(3)设降价后获得肉串的总利润为z元,令W=z−y.
∵200<x≤400,
∴z=(3.5−a−2)(1000−x)=(a−1.5)x+1500−1000a,
∴W=z−y=(a−2.5)x+1300−1000a.
∵0<a<1,
∴a−2.5<0,
∴W随x的增大而减小.
当x=400时,W的值最小.
由题意,可得z≥y,
∴W≥0,
即(a−2.5)×400+1300−1000a≥0,
解得a≤0.5,
∴a的最大值是0.5.