1. 若函数$ y= (m-3)x^{|m-2|}+3 $是一次函数,则$ m $的值为
1
.答案:1 [解析]由题意,得|m−2|=1,且m−3≠0,解得m=1.归纳总结 本题主要考查了一次函数的定义,关键是掌握形如y=kx+b(k,b是常数,k≠0)的函数,即一次函数
解析:
由题意,得$|m - 2| = 1$,且$m - 3 \neq 0$。
解$|m - 2| = 1$,得$m - 2 = 1$或$m - 2 = -1$,即$m = 3$或$m = 1$。
又因为$m - 3 \neq 0$,所以$m \neq 3$。
综上,$m = 1$。
1
解$|m - 2| = 1$,得$m - 2 = 1$或$m - 2 = -1$,即$m = 3$或$m = 1$。
又因为$m - 3 \neq 0$,所以$m \neq 3$。
综上,$m = 1$。
1
2.(2025·扬州高邮期末)已知函数$ y= (m-2)x^{m^2-3}-5 $是一次函数,则$ m= $
−2
.答案:−2 [解析]由题意,得m²−3=1且m−2≠0,解得m=±2且m≠2,所以m=−2.
解析:
由题意,得$m^2 - 3 = 1$且$m - 2 \neq 0$,
解得$m = \pm 2$且$m \neq 2$,
所以$m = -2$。
$-2$
解得$m = \pm 2$且$m \neq 2$,
所以$m = -2$。
$-2$
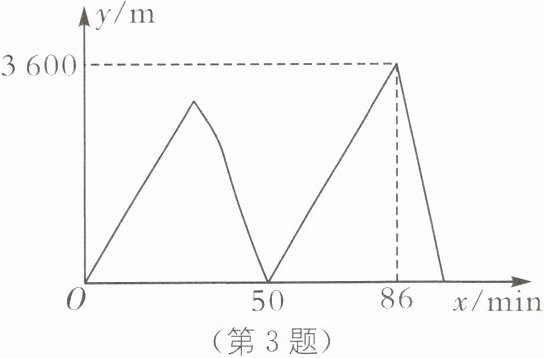
3. 新情境 行程问题 (2024·淄博中考)某日,甲、乙两人相约在一条笔直的健身道路上锻炼. 两人都从A地匀速出发,甲健步走向B地. 途中偶遇一位朋友,驻足交流10 min后,继续以原速步行前进;乙因故比甲晚出发30 min,跑步到达B地后立刻以原速返回,在返回途中与甲第二次相遇. 如图表示甲、乙两人之间的距离$ y(m) 与甲出发的时间 x(min) $之间的函数关系. 那么以下结论:①甲、乙两人第一次相遇时,乙的锻炼用时为20 min;②甲出发86 min时,甲、乙两人之间的距离达到最大值3600 m;③甲、乙两人第二次相遇的时间是在甲出发后100 min;④A,B两地之间的距离是11200 m. 其中正确的结论有(
A.①②③
B.①②④
C.①③④
D.②③④
B
).
A.①②③
B.①②④
C.①③④
D.②③④
答案:B [解析]①
∵乙比甲晚出发30min,且当x=50时,y=0,
∴乙出发50−30=20(min)时,两人第一次相遇,即甲、乙两人第一次相遇时,乙的锻炼用时为20min,结论①正确;②观察函数图象,可知当x=86时,y取得最大值,最大值为3600,
∴甲出发86min时,甲、乙两人之间的距离达到最大值3600m,结论②正确;③设甲的速度为xm/min,乙的速度为ym/min,根据题意,得{(50 - 10)x = (50 - 30)y,(86 - 30)y - (86 - 10)x = 3600},解得{x = 100,y = 200},
∴86 + $\frac{3600}{x + y}$ = 86 + $\frac{3600}{100 + 200}$ = 98,
∴甲、乙两人第二次相遇的时间是在甲出发后98min,结论③错误;④
∵200×(86−30)=11200(m),
∴A,B两地之间的距离是11200m,结论④正确.综上所述,正确的结论有①②④.故选B
∵乙比甲晚出发30min,且当x=50时,y=0,
∴乙出发50−30=20(min)时,两人第一次相遇,即甲、乙两人第一次相遇时,乙的锻炼用时为20min,结论①正确;②观察函数图象,可知当x=86时,y取得最大值,最大值为3600,
∴甲出发86min时,甲、乙两人之间的距离达到最大值3600m,结论②正确;③设甲的速度为xm/min,乙的速度为ym/min,根据题意,得{(50 - 10)x = (50 - 30)y,(86 - 30)y - (86 - 10)x = 3600},解得{x = 100,y = 200},
∴86 + $\frac{3600}{x + y}$ = 86 + $\frac{3600}{100 + 200}$ = 98,
∴甲、乙两人第二次相遇的时间是在甲出发后98min,结论③错误;④
∵200×(86−30)=11200(m),
∴A,B两地之间的距离是11200m,结论④正确.综上所述,正确的结论有①②④.故选B
4. 如图,直线$ y_1= x+3 $分别与x轴、y轴交于点A和点C,直线$ y_2= -x+3 $分别与x轴、y轴交于点B和点C,点$ P(m,2) 是 \triangle ABC $内部(包括边上)的一点,则m的最大值与最小值之差为( ).

A.1
B.2
C.4
D.6

A.1
B.2
C.4
D.6
答案:
B [解析]
∵点P(m,2)是△ABC内部(包括边上)的一点,
∴点P在直线y=2上,如图所示.
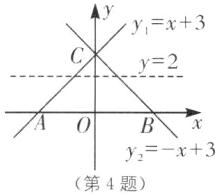
当P为直线y=2与直线y₂的交点时,m取最大值;当P为直线y=2与直线y₁的交点时,m取最小值.在y₂ = −x + 3中,令y₂ = 2,则x = 1,在y₁ = x + 3中,令y₁ = 2,则x = −1,
∴m的最大值为1,最小值为−1.则m的最大值与最小值之差为1−(−1)=2.故选B.思路引导 本题考查一次函数的图象与性质,要求符合题意的m值,关键要理解当P在何处时m存在最大值与最小值,由于P的纵坐标为2.故作出直线y=2有助于判断P的位置.
B [解析]
∵点P(m,2)是△ABC内部(包括边上)的一点,
∴点P在直线y=2上,如图所示.

当P为直线y=2与直线y₂的交点时,m取最大值;当P为直线y=2与直线y₁的交点时,m取最小值.在y₂ = −x + 3中,令y₂ = 2,则x = 1,在y₁ = x + 3中,令y₁ = 2,则x = −1,
∴m的最大值为1,最小值为−1.则m的最大值与最小值之差为1−(−1)=2.故选B.思路引导 本题考查一次函数的图象与性质,要求符合题意的m值,关键要理解当P在何处时m存在最大值与最小值,由于P的纵坐标为2.故作出直线y=2有助于判断P的位置.
5. 实验班原创 如图,直线$ l 是一次函数 y= kx+b(k≠0) $的图象,则$ b= $______.


2
答案:2 [解析]
∵直线y=kx+b与y轴交于点(0,2),
∴b=2.知识拓展 在一次函数y=kx+b中,k决定了直线的走向,b决定了直线与y轴的交点,因此由k和b的值可以确定出直线经过的象限,具体为:①当k>0,b>0时,函数图象经过第一、二、三象限;②当k>0,b<0时,函数图象经过第一、三、四象限;③当k<0,b>0时,函数图象经过第一、二、四象限;④当k<0,b<0时,函数图象经过第二、三、四象限
∵直线y=kx+b与y轴交于点(0,2),
∴b=2.知识拓展 在一次函数y=kx+b中,k决定了直线的走向,b决定了直线与y轴的交点,因此由k和b的值可以确定出直线经过的象限,具体为:①当k>0,b>0时,函数图象经过第一、二、三象限;②当k>0,b<0时,函数图象经过第一、三、四象限;③当k<0,b>0时,函数图象经过第一、二、四象限;④当k<0,b<0时,函数图象经过第二、三、四象限
6. 新情境 开展红色之旅研学活动 (2023·宁波中考)某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图(1))到爱国主义教育基地进行研学. 上午8:00,军车在离营地60 km的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程$ s(km) 与所用时间 t(h) $的函数关系如图(2)所示.
(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值;
(2)求部队官兵在仓库领取物资所用的时间.

(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值;
(2)求部队官兵在仓库领取物资所用的时间.

答案:
(1)由函数图象可得,大巴速度为$\frac{60 - 20}{1}$ = 40(km/h),
∴s = 40t + 20.当s = 100时,100 = 40t + 20,解得t = 2,
∴a的值为2,
∴大巴离营地的路程s与所用时间t的函数表达式为s = 40t + 20,a的值为2.
(2)由函数图象可得,军车速度为60÷1 = 60(km/h).设部队官兵在仓库领取物资所用的时间为xh,根据题意,得60(2 - x) = 100,解得x = $\frac{1}{3}$.故部队官兵在仓库领取物资所用的时间为$\frac{1}{3}$h.
(1)由函数图象可得,大巴速度为$\frac{60 - 20}{1}$ = 40(km/h),
∴s = 40t + 20.当s = 100时,100 = 40t + 20,解得t = 2,
∴a的值为2,
∴大巴离营地的路程s与所用时间t的函数表达式为s = 40t + 20,a的值为2.
(2)由函数图象可得,军车速度为60÷1 = 60(km/h).设部队官兵在仓库领取物资所用的时间为xh,根据题意,得60(2 - x) = 100,解得x = $\frac{1}{3}$.故部队官兵在仓库领取物资所用的时间为$\frac{1}{3}$h.