7. 一题多问 (2024·天津中考)已知小华的家、画社、文化广场依次在同一条直线上,画社离家0.6 km,文化广场离家1.5 km. 小华从家出发,先匀速骑行了4 min到画社,在画社停留了15 min,之后匀速骑行了6 min到文化广场,在文化广场停留6 min后,再匀速步行了20 min返回家. 如图,图中x表示时间,y表示离家的距离. 图象反映了这个过程中小华离家的距离与时间之间的对应关系.
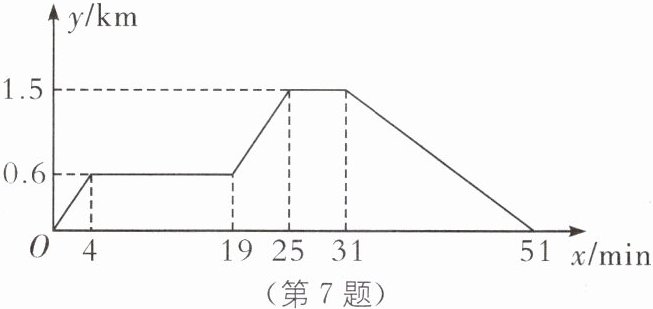
请根据相关信息,回答下列问题:
(1)①填表:
|小华离开家的时间/min|1|4|13|30|
|小华离家的距离/km|

②填空:小华从文化广场返回家的速度为
③当$ 0≤x≤25 $时,请直接写出小华离家的距离y关于时间x的函数表达式.
(2)当小华离开家8 min时,他的爸爸也从家出发匀速步行了20 min直接到达了文化广场,那么从画社到文化广场的途中(0.6<y<1.5)两人相遇时离家的距离是多少?(直接写出结果即可)

请根据相关信息,回答下列问题:
(1)①填表:
|小华离开家的时间/min|1|4|13|30|
|小华离家的距离/km|
0.15
|0.6|0.6
|1.5
|
②填空:小华从文化广场返回家的速度为
0.075
km/min.③当$ 0≤x≤25 $时,请直接写出小华离家的距离y关于时间x的函数表达式.
当0≤x≤4时,y=0.15x;当4<x≤19时,y=0.6;当19<x≤25时,y=0.15x-2.25
(2)当小华离开家8 min时,他的爸爸也从家出发匀速步行了20 min直接到达了文化广场,那么从画社到文化广场的途中(0.6<y<1.5)两人相遇时离家的距离是多少?(直接写出结果即可)
1.05km
答案:
(1)①由图象可填表:
小华离开家的时间/min 1 4 13 30
小华离家的距离/km 0.15 0.6 0.6 1.5
②0.075
③小华从家到画社的速度为$\frac{0.6}{4}$ = 0.15(km/min),小华从画社到文化广场的速度为$\frac{1.5 - 0.6}{25 - 19}$ = 0.15(km/min),当0≤x≤4时,y = 0.15x;当4<x≤19时,y = 0.6;当19<x≤25时,y = 0.15(x - 19) + 0.6 = 0.15x - 2.25,
∴当0≤x≤25时,y与x的函数表达式为
y = {0.15x(0 ≤ x ≤ 4),0.6(4 < x ≤ 19),0.15x - 2.25(19 < x ≤ 25)}
(2)
∵爸爸的速度为$\frac{1.5}{20}$ = 0.075(km/min),
∴设小华出发x分钟时和爸爸相遇.根据题意得0.15x - 2.25 = 0.075(x - 8),解得x = 22,
∴0.15×22 - 2.25 = 1.05(km),故从画社到文化广场的途中两人相遇时离家的距离为1.05km.
(1)①由图象可填表:
小华离开家的时间/min 1 4 13 30
小华离家的距离/km 0.15 0.6 0.6 1.5
②0.075
③小华从家到画社的速度为$\frac{0.6}{4}$ = 0.15(km/min),小华从画社到文化广场的速度为$\frac{1.5 - 0.6}{25 - 19}$ = 0.15(km/min),当0≤x≤4时,y = 0.15x;当4<x≤19时,y = 0.6;当19<x≤25时,y = 0.15(x - 19) + 0.6 = 0.15x - 2.25,
∴当0≤x≤25时,y与x的函数表达式为
y = {0.15x(0 ≤ x ≤ 4),0.6(4 < x ≤ 19),0.15x - 2.25(19 < x ≤ 25)}
(2)
∵爸爸的速度为$\frac{1.5}{20}$ = 0.075(km/min),
∴设小华出发x分钟时和爸爸相遇.根据题意得0.15x - 2.25 = 0.075(x - 8),解得x = 22,
∴0.15×22 - 2.25 = 1.05(km),故从画社到文化广场的途中两人相遇时离家的距离为1.05km.
8. 中考新考法 新定义问题 若定义一种新运算:$ a⊗b= \begin{cases} a-b(a≥2b), \\ a+b-6(a<2b). \end{cases} $例如:$ 3⊗1= 3-1= 2 $;$ 5⊗4= 5+4-6= 3 $,则函数$ y= (x+2)⊗(x-1) $的图象大致是(

A.
B.
C.
D.
A
).
A.
B.
C.
D.
答案:A [解析]
∵当x + 2 ≥ 2(x - 1)时,x ≤ 4,
∴当x ≤ 4时,(x + 2)⊗(x - 1) = (x + 2) - (x - 1) = x + 2 - x + 1 = 3,即y = 3,函数图象为一条平行于x轴的直线;当x>4时,(x + 2)⊗(x - 1) = (x + 2) + (x - 1) - 6 = x + 2 + x - 1 - 6 = 2x - 5,即y = 2x - 5.又k = 2>0,
∴当x>4时,y = 2x - 5,函数图象从左向右逐渐上升,y随x的增大而增大.综上所述,A选项符合题意.故选A 思路引导 解答本题时需要先根据新定义求出函数图象的自变量的取值范围,然后根据新定义分别求出不同自变量取值范围内的函数表达式,再根据函数的表达式即可得到函数的图象.
∵当x + 2 ≥ 2(x - 1)时,x ≤ 4,
∴当x ≤ 4时,(x + 2)⊗(x - 1) = (x + 2) - (x - 1) = x + 2 - x + 1 = 3,即y = 3,函数图象为一条平行于x轴的直线;当x>4时,(x + 2)⊗(x - 1) = (x + 2) + (x - 1) - 6 = x + 2 + x - 1 - 6 = 2x - 5,即y = 2x - 5.又k = 2>0,
∴当x>4时,y = 2x - 5,函数图象从左向右逐渐上升,y随x的增大而增大.综上所述,A选项符合题意.故选A 思路引导 解答本题时需要先根据新定义求出函数图象的自变量的取值范围,然后根据新定义分别求出不同自变量取值范围内的函数表达式,再根据函数的表达式即可得到函数的图象.
9.(2023·大连中考)某学校体育队开展跑步训练,体育老师将队员分成男、女两组. 两组队员从同一地点同向先后出发,女子组跑了80 m时,男子组恰好跑了50 m. 此后两组队员开始匀速跑,直到终点. 已知男子组匀速跑的速度为4.5 m/s. 男、女两组队员跑步的路程y(单位:m)与匀速跑的时间x(单位:s)的图象如图所示.
(1)此次跑步训练的全程是
(2)求男子组追上女子组时,两组队员离终点的路程.

(1)此次跑步训练的全程是
500
m;(2)求男子组追上女子组时,两组队员离终点的路程.

女子组的速度为(500 - 80)÷120 = 3.5(m/s),则男子组队员跑步的路程为y = 4.5x + 50,女子组队员跑步的路程为y = 3.5x + 80,联立,得{y = 4.5x + 50,y = 3.5x + 80},解得{x = 30,y = 185},
∴500 - 185 = 315(米).
∴男子组追上女子组时,两组队员离终点的路程为315米.
∴500 - 185 = 315(米).
∴男子组追上女子组时,两组队员离终点的路程为315米.
答案:
(1)500 [解析]100×4.5 + 50 = 500(米).
(2)女子组的速度为(500 - 80)÷120 = 3.5(m/s),则男子组队员跑步的路程为y = 4.5x + 50,女子组队员跑步的路程为y = 3.5x + 80,联立,得{y = 4.5x + 50,y = 3.5x + 80},解得{x = 30,y = 185},
∴500 - 185 = 315(米).
∴男子组追上女子组时,两组队员离终点的路程为315米.
(1)500 [解析]100×4.5 + 50 = 500(米).
(2)女子组的速度为(500 - 80)÷120 = 3.5(m/s),则男子组队员跑步的路程为y = 4.5x + 50,女子组队员跑步的路程为y = 3.5x + 80,联立,得{y = 4.5x + 50,y = 3.5x + 80},解得{x = 30,y = 185},
∴500 - 185 = 315(米).
∴男子组追上女子组时,两组队员离终点的路程为315米.