10.(2025·镇江丹阳期末)已知一次函数$ y= kx+b(k≠0) 的图象经过点 A(0,-3) $,且与正比例函数$ y= \frac{1}{2}x 的图象相交于点 B(2,m) $. 求:
(1)m的值;
(2)k,b的值;
(3)$ \triangle AOB $的面积.
(1)m的值;
(2)k,b的值;
(3)$ \triangle AOB $的面积.
答案:
(1)
∵点B(2,m)在正比例函数y = $\frac{1}{2}x$的图象上,
∴m = $\frac{1}{2}$×2 = 1.
(2)
∵一次函数y = kx + b(k≠0)的图象经过点A(0, - 3),B(2,1),{b = - 3,2k + b = 1},解得{k = 2,b = - 3},
∴k = 2,b = - 3.
(3)S△AOB = $\frac{1}{2}$×3×2 = 3.
(1)
∵点B(2,m)在正比例函数y = $\frac{1}{2}x$的图象上,
∴m = $\frac{1}{2}$×2 = 1.
(2)
∵一次函数y = kx + b(k≠0)的图象经过点A(0, - 3),B(2,1),{b = - 3,2k + b = 1},解得{k = 2,b = - 3},
∴k = 2,b = - 3.
(3)S△AOB = $\frac{1}{2}$×3×2 = 3.
11.(2023·天津中考)已知学生宿舍、文具店、体育场依次在同一条直线上,文具店离宿舍0.6 km,体育场离宿舍1.2 km,小强从宿舍出发,先用了10 min匀速跑步去体育场,在体育场锻炼了30 min,之后匀速步行了10 min到文具店买笔,在文具店停留10 min后,用了20 min匀速散步返回宿舍,下面图中x表示时间,y表示离宿舍的距离. 图象反映了这个过程中小强离宿舍的距离与时间之间的对应关系.
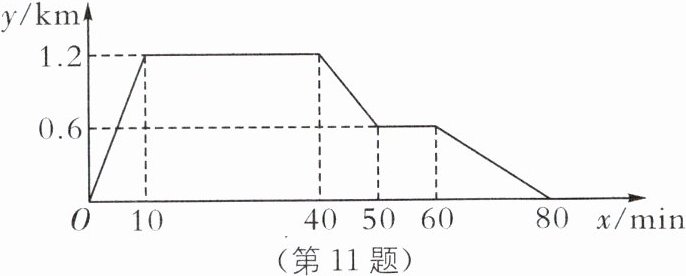
请根据相关信息,回答下列问题:
(1)①填表:
|小强离开宿舍的时间/min|1|10|20|60|
|小强离宿舍的距离/km|

②填空:小强从体育场到文具店的速度为
③当$ 50≤x≤80 $时,请直接写出小强离宿舍的距离y关于时间x的函数表达式.
(2)当小强离开体育场15 min时,同宿舍的小明也从体育场出发匀速步行直接回宿舍,如果小明的速度为0.06 km/min,那么他在回宿舍的途中遇到小强时离宿舍的距离是多少?(直接写出结果即可)

请根据相关信息,回答下列问题:
(1)①填表:
|小强离开宿舍的时间/min|1|10|20|60|
|小强离宿舍的距离/km|
0.12
|1.2|1.2
|0.6
|
②填空:小强从体育场到文具店的速度为
0.06
km/min.③当$ 50≤x≤80 $时,请直接写出小强离宿舍的距离y关于时间x的函数表达式.
当50≤x≤60时,y=0.6;当60<x≤80时,y=2.4-0.03x
(2)当小强离开体育场15 min时,同宿舍的小明也从体育场出发匀速步行直接回宿舍,如果小明的速度为0.06 km/min,那么他在回宿舍的途中遇到小强时离宿舍的距离是多少?(直接写出结果即可)
0.3 km
答案:
(1)①0.12 1.2 0.6 [解析]由图象可知,小强从宿舍到体育场的速度为1.2÷10 = 0.12(km/min),
∴当小强离开宿舍1min时,小强离宿舍的距离为0.12×1 = 0.12(km);当小强离开宿舍20min时,小强离宿舍的距离为1.2km;当小强离开宿舍60min时,小强离宿舍的距离为0.6km.
小强离开宿舍的时间/min 1 10 20 60
小强离宿舍的距离/km 0.12 1.2 1.2 0.6
②0.06 [解析]由图象知,小强从体育场到文具店的速度为$\frac{1.2 - 0.6}{50 - 40}$ = 0.06(km/min).
③当50<x≤60时,y = 0.6;小强从文具店到宿舍时的速度为$\frac{0.6}{80 - 60}$ = 0.03(km/min),
∴当60<x≤80时,y = 2.4 - 0.03x.综上所述,y关于x的函数表达式为y = {0.6(50 < x ≤ 60),2.4 - 0.03x(60 < x ≤ 80)}
(2)根据题意,当小强离开体育场15min时,小强到达文具店并停留了5min,设小明从体育场出发x分钟后与小强相遇,则0.06x = 0.03(x - 5) + 0.6,解得x = 15,
∴1.2 - 0.06×15 = 0.3(km),
∴离宿舍的距离是0.3km.
(1)①0.12 1.2 0.6 [解析]由图象可知,小强从宿舍到体育场的速度为1.2÷10 = 0.12(km/min),
∴当小强离开宿舍1min时,小强离宿舍的距离为0.12×1 = 0.12(km);当小强离开宿舍20min时,小强离宿舍的距离为1.2km;当小强离开宿舍60min时,小强离宿舍的距离为0.6km.
小强离开宿舍的时间/min 1 10 20 60
小强离宿舍的距离/km 0.12 1.2 1.2 0.6
②0.06 [解析]由图象知,小强从体育场到文具店的速度为$\frac{1.2 - 0.6}{50 - 40}$ = 0.06(km/min).
③当50<x≤60时,y = 0.6;小强从文具店到宿舍时的速度为$\frac{0.6}{80 - 60}$ = 0.03(km/min),
∴当60<x≤80时,y = 2.4 - 0.03x.综上所述,y关于x的函数表达式为y = {0.6(50 < x ≤ 60),2.4 - 0.03x(60 < x ≤ 80)}
(2)根据题意,当小强离开体育场15min时,小强到达文具店并停留了5min,设小明从体育场出发x分钟后与小强相遇,则0.06x = 0.03(x - 5) + 0.6,解得x = 15,
∴1.2 - 0.06×15 = 0.3(km),
∴离宿舍的距离是0.3km.
12.(2023·金华中考)兄妹俩放学后沿图(1)中的马路从学校出发,到书吧看书后回家,哥哥步行先出发,途中速度保持不变;妹妹骑车,到书吧前的速度为200米/分,图(2)中的图象分别表示两人离学校的路程s(米)与哥哥离开学校的时间t(分)的函数关系.
(1)求哥哥步行的速度.
(2)已知妹妹比哥哥迟2分钟到书吧.
①求图中a的值.
②妹妹在书吧待了10分钟后回家,速度是哥哥的1.6倍,能否在哥哥到家前追上哥哥?若能,求追上时兄妹俩离家还有多远;若不能,说明理由.

(1)求哥哥步行的速度.
(2)已知妹妹比哥哥迟2分钟到书吧.
①求图中a的值.
②妹妹在书吧待了10分钟后回家,速度是哥哥的1.6倍,能否在哥哥到家前追上哥哥?若能,求追上时兄妹俩离家还有多远;若不能,说明理由.

答案:
(1)由A(8,800)可知哥哥的速度为800÷8 = 100(米/分).
(2)①
∵妹妹骑车到书吧前的速度为200米/分,
∴妹妹所用时间t为800÷200 = 4(分).
∵妹妹比哥哥迟2分钟到书吧,
∴a = 8 + 2 - 4 = 6.
②由
(1)可知,哥哥的速度为100米/分,
∴设BC所在直线的表达式为s₁ = 100t + b,将B(17,800)代入,得800 = 100×17 + b,解得b = - 900,
∴BC所在直线的表达式为s₁ = 100t - 900.当s₁ = 1900时,t哥哥 = 28.
∵返回时妹妹的速度是哥哥的1.6倍,
∴妹妹的速度是160米/分,
∴设妹妹返回时的表达式为s₂ = 160t + n,将F(20,800)代入,得800 = 160×20 + n,解得n = - 2400,
∴s₂ = 160t - 2400.令s₁ = s₂,则有100t - 900 = 160t - 2400,解得t = 25<28,
∴妹妹能追上哥哥,此时哥哥所走的路程为800 + (25 - 17)×100 = 1600(米),兄妹俩离家还有1900 - 1600 = 300(米).故妹妹能追上哥哥,追上时兄妹俩离家300米远.
(1)由A(8,800)可知哥哥的速度为800÷8 = 100(米/分).
(2)①
∵妹妹骑车到书吧前的速度为200米/分,
∴妹妹所用时间t为800÷200 = 4(分).
∵妹妹比哥哥迟2分钟到书吧,
∴a = 8 + 2 - 4 = 6.
②由
(1)可知,哥哥的速度为100米/分,
∴设BC所在直线的表达式为s₁ = 100t + b,将B(17,800)代入,得800 = 100×17 + b,解得b = - 900,
∴BC所在直线的表达式为s₁ = 100t - 900.当s₁ = 1900时,t哥哥 = 28.
∵返回时妹妹的速度是哥哥的1.6倍,
∴妹妹的速度是160米/分,
∴设妹妹返回时的表达式为s₂ = 160t + n,将F(20,800)代入,得800 = 160×20 + n,解得n = - 2400,
∴s₂ = 160t - 2400.令s₁ = s₂,则有100t - 900 = 160t - 2400,解得t = 25<28,
∴妹妹能追上哥哥,此时哥哥所走的路程为800 + (25 - 17)×100 = 1600(米),兄妹俩离家还有1900 - 1600 = 300(米).故妹妹能追上哥哥,追上时兄妹俩离家300米远.