1. (2024·呼伦贝尔中考)点P(x,y)在直线$y= -\frac{3}{4}x+4$上,坐标(x,y)是二元一次方程5x-6y= 33的解,则点P的位置在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
).A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:D [解析]解方程组$\left\{\begin{array}{l} y=-\dfrac {3}{4}x+4,\\ 5x-6y=33,\end{array}\right.$得$\left\{\begin{array}{l} x=6,\\ y=-\dfrac {1}{2},\end{array}\right.$
$\therefore P\left(6,-\dfrac {1}{2}\right)$,$\therefore P$在第四象限。故选D。
$\therefore P\left(6,-\dfrac {1}{2}\right)$,$\therefore P$在第四象限。故选D。
2. 已知一次函数y= 2x+m和y= 3x+2m的图象的交点的横坐标为1,则m=
-1
.答案:-1 [解析]把$x=1$代入$y=2x+m$,得$y=2+m$;把$x=1$代入$y=3x+2m$,得$y=3+2m$。
所以$2+m=3+2m$,解得$m=-1$。
所以$2+m=3+2m$,解得$m=-1$。
3. (2024·南通崇川区启秀中学月考)已知点A(a,b),B(c,d)在第一象限,a,b,c,d均为整数,且$\begin{cases} x= a, \\ y= b, \end{cases} \begin{cases} x= c, \\ y= d \end{cases} $满足方程3x+2y= 13.
(1)求A,B两点坐标;
(2)若在直线AB上的点横、纵坐标均为上面方程的解,则直线AB叫作方程3x+2y= 13的图象,已知点P(m,n)是线段AB上一点,写出m和n的关系式(用n表示m),并写出m的取值范围.
(1)求A,B两点坐标;
(2)若在直线AB上的点横、纵坐标均为上面方程的解,则直线AB叫作方程3x+2y= 13的图象,已知点P(m,n)是线段AB上一点,写出m和n的关系式(用n表示m),并写出m的取值范围.
答案:
(1)方程$3x+2y=13$,解得$x=\dfrac {13-2y}{3}$,
当$y=2$时,$x=3$;$y=5$时,$x=1$,
则方程的所有正整数解为$\left\{\begin{array}{l} x=3,\\ y=2,\end{array}\right. \left\{\begin{array}{l} x=1,\\ y=5.\end{array}\right.$
$\because$点$A(a,b)$,$B(c,d)$在第一象限,$a$,$b$,$c$,$d$均为整数,且$\left\{\begin{array}{l} x=a,\\ y=b,\end{array}\right. \left\{\begin{array}{l} x=c,\\ y=d\end{array}\right.$满足方程$3x+2y=13$,
$\therefore A(1,5)$,$B(3,2)$或$A(3,2)$,$B(1,5)$。
(2)$\because$点$P(m,n)$是线段$AB$上一点,
$\therefore m=\dfrac {13-2n}{3}(1\leqslant m\leqslant 3)$。
(1)方程$3x+2y=13$,解得$x=\dfrac {13-2y}{3}$,
当$y=2$时,$x=3$;$y=5$时,$x=1$,
则方程的所有正整数解为$\left\{\begin{array}{l} x=3,\\ y=2,\end{array}\right. \left\{\begin{array}{l} x=1,\\ y=5.\end{array}\right.$
$\because$点$A(a,b)$,$B(c,d)$在第一象限,$a$,$b$,$c$,$d$均为整数,且$\left\{\begin{array}{l} x=a,\\ y=b,\end{array}\right. \left\{\begin{array}{l} x=c,\\ y=d\end{array}\right.$满足方程$3x+2y=13$,
$\therefore A(1,5)$,$B(3,2)$或$A(3,2)$,$B(1,5)$。
(2)$\because$点$P(m,n)$是线段$AB$上一点,
$\therefore m=\dfrac {13-2n}{3}(1\leqslant m\leqslant 3)$。
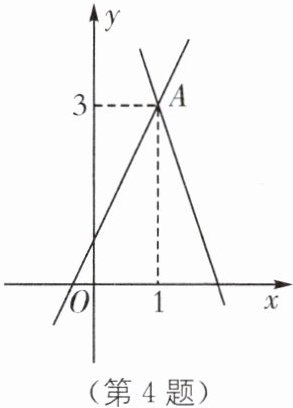
4. (教材P170例·变式)如图,在平面直角坐标系中,直线y= 2x+b与直线y= -3x+6相交于点A,则关于x,y的二元一次方程组$\begin{cases} y= 2x+b, \\ y= -3x+6 \end{cases} 的解是(
B
).A. \begin{cases} x= 2, \\ y= 0 \end{cases} B. \begin{cases} x= 1, \\ y= 3 \end{cases} C. \begin{cases} x= -1, \\ y= 9 \end{cases} D. \begin{cases} x= 3, \\ y= 1 \end{cases} $
答案:B [解析]由图象可得两直线的交点坐标是$(1,3)$,
$\therefore$方程组$\left\{\begin{array}{l} y=2x+b,\\ y=-3x+6\end{array}\right.$的解为$\left\{\begin{array}{l} x=1,\\ y=3.\end{array}\right.$故选B。
归纳总结 本题考查一次函数与二元一次方程组的关系,解题的关键是理解两直线交点坐标中$x$与$y$的值为两直线对应的两个函数关系式组成的方程组的解。
$\therefore$方程组$\left\{\begin{array}{l} y=2x+b,\\ y=-3x+6\end{array}\right.$的解为$\left\{\begin{array}{l} x=1,\\ y=3.\end{array}\right.$故选B。
归纳总结 本题考查一次函数与二元一次方程组的关系,解题的关键是理解两直线交点坐标中$x$与$y$的值为两直线对应的两个函数关系式组成的方程组的解。
5. 如图,直线y= kx(k≠0)与y= ax+b(a≠0)在第二象限交于A,y= ax+b交x轴于B,且AB= AO,BO= 8,$S_{\triangle ABO}= 12,则方程组\begin{cases} y= kx, \\ y= ax+b \end{cases} 的解为( ).A. \begin{cases} x= -4, \\ y= 3 \end{cases} B. \begin{cases} x= -3, \\ y= 4 \end{cases} C. \begin{cases} x= -3, \\ y= -4 \end{cases} D. \begin{cases} x= -4, \\ y= -3 \end{cases} $


答案:
A [解析]如图,过点$A$作$AH\perp x$轴于点$H$。
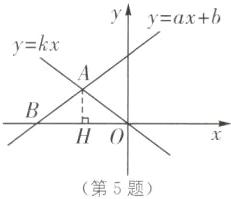
$\because AB=AO$,$\therefore BH=OH=\dfrac {1}{2}OB=4$。
$\because S_{\triangle ABO}=12$,$\therefore \dfrac {1}{2}OB\cdot AH=12$,
$\therefore AH=\dfrac {12× 2}{8}=3$,$\therefore A(-4,3)$,
$\therefore$方程组$\left\{\begin{array}{l} y=kx,\\ y=ax+b\end{array}\right.$的解为$\left\{\begin{array}{l} x=-4,\\ y=3.\end{array}\right.$故选A。
A [解析]如图,过点$A$作$AH\perp x$轴于点$H$。

$\because AB=AO$,$\therefore BH=OH=\dfrac {1}{2}OB=4$。
$\because S_{\triangle ABO}=12$,$\therefore \dfrac {1}{2}OB\cdot AH=12$,
$\therefore AH=\dfrac {12× 2}{8}=3$,$\therefore A(-4,3)$,
$\therefore$方程组$\left\{\begin{array}{l} y=kx,\\ y=ax+b\end{array}\right.$的解为$\left\{\begin{array}{l} x=-4,\\ y=3.\end{array}\right.$故选A。
6. (2025·扬州宝应期末)已知直线y= 2x+1与y= kx-b的交点为(-2,a),则方程组$\begin{cases} y= 2x+1, \\ y= kx-b \end{cases} $的解为______
$\left\{\begin{array}{l} x=-2,\\ y=-3\end{array}\right.$
.答案:$\left\{\begin{array}{l} x=-2,\\ y=-3\end{array}\right.$ [解析]把$(-2,a)$代入$y=2x+1$,得$a=(-2)× 2+1=-3$,即直线$y=2x+1$与$y=kx-b$的交点为$(-2,-3)$,则方程组$\left\{\begin{array}{l} y=2x+1,\\ y=kx-b\end{array}\right.$的解为$\left\{\begin{array}{l} x=-2,\\ y=-3.\end{array}\right.$
解析:
$\left\{\begin{array}{l} x=-2\\ y=-3\end{array}\right.$
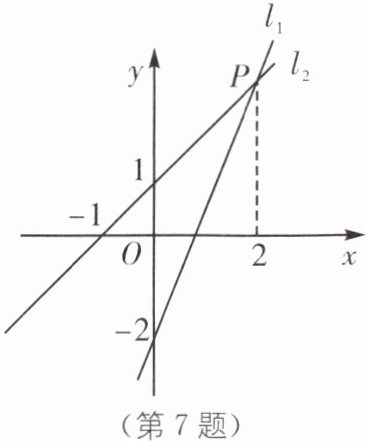
7. (2024·山东菏泽东明期末)如图,过点(0,-2)的直线l_{1}:y= kx+b(k≠0)与直线l_{2}:y= x+1交于点P(2,m).
(1)求点P的坐标和直线l_{1}的表达式;
(2)根据图象直接写出方程组$\begin{cases} y= kx+b, \\ y= x+1 \end{cases} $的解.
(1)求点P的坐标和直线l_{1}的表达式;
(2)根据图象直接写出方程组$\begin{cases} y= kx+b, \\ y= x+1 \end{cases} $的解.

答案:
(1)把$P(2,m)$代入$y=x+1$,得$m=3$,
则点$P$的坐标为$(2,3)$。
把$(0,-2)$,$(2,3)$代入$y=kx+b$,得$\left\{\begin{array}{l} b=-2,\\ 2k+b=3,\end{array}\right.$
解得$\left\{\begin{array}{l} k=\dfrac {5}{2},\\ b=-2.\end{array}\right.$所以直线$l_{1}$的表达式为$y=\dfrac {5}{2}x-2$。
(2)因为直线$l_{1}:y=kx+b(k\neq 0)$与直线$l_{2}:y=x+1$交于点$P(2,3)$,所以方程组$\left\{\begin{array}{l} y=kx+b,\\ y=x+1\end{array}\right.$的解为$\left\{\begin{array}{l} x=2,\\ y=3.\end{array}\right.$
(1)把$P(2,m)$代入$y=x+1$,得$m=3$,
则点$P$的坐标为$(2,3)$。
把$(0,-2)$,$(2,3)$代入$y=kx+b$,得$\left\{\begin{array}{l} b=-2,\\ 2k+b=3,\end{array}\right.$
解得$\left\{\begin{array}{l} k=\dfrac {5}{2},\\ b=-2.\end{array}\right.$所以直线$l_{1}$的表达式为$y=\dfrac {5}{2}x-2$。
(2)因为直线$l_{1}:y=kx+b(k\neq 0)$与直线$l_{2}:y=x+1$交于点$P(2,3)$,所以方程组$\left\{\begin{array}{l} y=kx+b,\\ y=x+1\end{array}\right.$的解为$\left\{\begin{array}{l} x=2,\\ y=3.\end{array}\right.$