1. (2024·甘南州中考)某网络经销商购进了一批A型钥匙扣和B型钥匙扣.已知购进A型钥匙扣50个、B型钥匙扣30个共需870元,购进A型钥匙扣30个、B型钥匙扣50个共需810元.
(1)每个A型钥匙扣和B型钥匙扣的进价分别是多少元?
(2)该经销商决定购进A型钥匙扣和B型钥匙扣共100个,投入资金不超过1000元,并将A型钥匙扣的售价定为每个20元,B型钥匙扣的售价定为每个15元,请问如何进货可以使该经销商获得最大利润?最大利润是多少元?
(1)每个A型钥匙扣和B型钥匙扣的进价分别是多少元?
(2)该经销商决定购进A型钥匙扣和B型钥匙扣共100个,投入资金不超过1000元,并将A型钥匙扣的售价定为每个20元,B型钥匙扣的售价定为每个15元,请问如何进货可以使该经销商获得最大利润?最大利润是多少元?
答案:1.
(1)设每个A型钥匙扣的进价为x元,B型钥匙扣的进价为y元.根据题意,得{50x+30y=870,30x+50y=810,解得{x=12,y=9,故每个A型钥匙扣的进价为12元,B型钥匙扣的进价为9元.
(2)设购进A型钥匙扣a个,则B型钥匙扣(100−a)个,利润为W元,根据题意,得W=(20−12)a+(15−9)(100−a)=2a+600.
∵12a+9(100−a)≤1 000,
∴a≤33$\frac{1}{3}$,且a为非负整数.
∵2>0,
∴W随着a的增大而增大,
∴当a=33时,W最大,最大值为2×33+600=666,
∴该经销商应购进A型钥匙扣33个,B型钥匙扣67个,可获得最大利润,最大利润为666元.
(1)设每个A型钥匙扣的进价为x元,B型钥匙扣的进价为y元.根据题意,得{50x+30y=870,30x+50y=810,解得{x=12,y=9,故每个A型钥匙扣的进价为12元,B型钥匙扣的进价为9元.
(2)设购进A型钥匙扣a个,则B型钥匙扣(100−a)个,利润为W元,根据题意,得W=(20−12)a+(15−9)(100−a)=2a+600.
∵12a+9(100−a)≤1 000,
∴a≤33$\frac{1}{3}$,且a为非负整数.
∵2>0,
∴W随着a的增大而增大,
∴当a=33时,W最大,最大值为2×33+600=666,
∴该经销商应购进A型钥匙扣33个,B型钥匙扣67个,可获得最大利润,最大利润为666元.
2. (2023·青岛中考)某服装店经销A,B两种T恤衫,进价和售价如下表所示:
| 品名 | A | B |
| 进价/(元/件) | 45 | 60 |
| 售价/(元/件) | 66 | 90 |
(1)第一次进货时,服装店用6000元购进A,B两种T恤衫共120件,全部售完获利多少元?
(2)受市场因素影响,第二次进货时,A种T恤衫进价每件上涨了5元,B种T恤衫进价每件上涨了10元,但两种T恤衫的售价不变.服装店计划购进A,B两种T恤衫共150件,且B种T恤衫的购进量不超过A种T恤衫购进量的2倍.设此次购进A种T恤衫m件,两种T恤衫全部售完可获利W元.
①请求出W与m的函数关系式.
②服装店第二次获利能否超过第一次获利?请说明理由.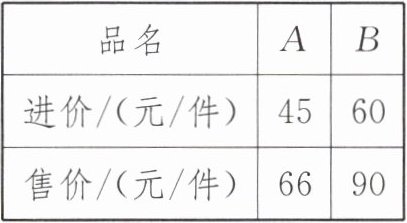 精题详解
精题详解
| 品名 | A | B |
| 进价/(元/件) | 45 | 60 |
| 售价/(元/件) | 66 | 90 |
(1)第一次进货时,服装店用6000元购进A,B两种T恤衫共120件,全部售完获利多少元?
(2)受市场因素影响,第二次进货时,A种T恤衫进价每件上涨了5元,B种T恤衫进价每件上涨了10元,但两种T恤衫的售价不变.服装店计划购进A,B两种T恤衫共150件,且B种T恤衫的购进量不超过A种T恤衫购进量的2倍.设此次购进A种T恤衫m件,两种T恤衫全部售完可获利W元.
①请求出W与m的函数关系式.
②服装店第二次获利能否超过第一次获利?请说明理由.
 精题详解
精题详解答案:2.
(1)设购进A种T恤衫x件,购进B种T恤衫y件,由题意,得{x+y=120,45x+60y=6 000,解得{x=80,y=40,
∴全部售完获利(66−45)×80+(90−60)×40=1 680+1 200=2 880(元).
(2)①设第二次购进A种T恤衫m件,则购进B种T恤衫(150−m)件,由题意,得150−m≤2m,即m≥50,
∴W=(66−45−5)m+(90−60−10)(150−m)=−4m+3 000(50≤m≤150).
②服装店第二次获利不能超过第一次获利.理由如下:由①可知,W=−4m+3 000(50≤m≤150).
∵−4<0,
∴W随m的增大而减小,
∴当m=50时,W取最大值,W最大=−4×50+3 000=2 800.
∵2 800<2 880,
∴服装店第二次获利不能超过第一次获利.
(1)设购进A种T恤衫x件,购进B种T恤衫y件,由题意,得{x+y=120,45x+60y=6 000,解得{x=80,y=40,
∴全部售完获利(66−45)×80+(90−60)×40=1 680+1 200=2 880(元).
(2)①设第二次购进A种T恤衫m件,则购进B种T恤衫(150−m)件,由题意,得150−m≤2m,即m≥50,
∴W=(66−45−5)m+(90−60−10)(150−m)=−4m+3 000(50≤m≤150).
②服装店第二次获利不能超过第一次获利.理由如下:由①可知,W=−4m+3 000(50≤m≤150).
∵−4<0,
∴W随m的增大而减小,
∴当m=50时,W取最大值,W最大=−4×50+3 000=2 800.
∵2 800<2 880,
∴服装店第二次获利不能超过第一次获利.
3. 某果品公司急需将一批不易存放的水果从A市运到B市销售.现有三家运输公司可供选择,这三家运输公司提供的信息如下:
| 运输单位 | 运输速度/(千米/时) | 运输费用/(元/千米) | 包装与装卸时间/小时 | 包装与装卸费用/元 |
| 甲公司 | 60 | 6 | 4 | 1500 |
| 乙公司 | 50 | 8 | 2 | 1000 |
| 丙公司 | 100 | 10 | 3 | 700 |

解答下列问题:
(1)若乙、丙两家公司的包装与装卸及运输的费用总和恰好是甲公司的2倍,求A,B两市的距离(精确到个位);
(2)如果A,B两市的距离为s千米,且这批水果在包装与装卸以及运输过程中的损耗为300元/小时,那么要使果品公司支付的总费用(包装与装卸费用、运输费用及损耗三项之和)最小,应选择哪家运输公司?
| 运输单位 | 运输速度/(千米/时) | 运输费用/(元/千米) | 包装与装卸时间/小时 | 包装与装卸费用/元 |
| 甲公司 | 60 | 6 | 4 | 1500 |
| 乙公司 | 50 | 8 | 2 | 1000 |
| 丙公司 | 100 | 10 | 3 | 700 |

解答下列问题:
(1)若乙、丙两家公司的包装与装卸及运输的费用总和恰好是甲公司的2倍,求A,B两市的距离(精确到个位);
(2)如果A,B两市的距离为s千米,且这批水果在包装与装卸以及运输过程中的损耗为300元/小时,那么要使果品公司支付的总费用(包装与装卸费用、运输费用及损耗三项之和)最小,应选择哪家运输公司?
答案:3.
(1)设A,B两市的距离为x千米,则三家运输公司包装与装卸及运输的费用分别是甲公司(6x+1 500)元,乙公司(8x+1 000)元,丙公司(10x+700)元,依题意,得(8x+1 000)+(10x+700)=2×(6x+1 500),解得x=216$\frac{2}{3}$≈217.故A,B两市的距离约为217千米.
(2)设选择甲、乙、丙三家运输公司的总费用分别为y₁元、y₂元、y₃元,由于三家运输公司包装与装卸及运输所需的时间分别为甲公司($\frac{s}{60}$+4)小时,乙公司($\frac{s}{50}$+2)小时,丙公司($\frac{s}{100}$+3)小时,所以y₁=6s+1 500+($\frac{s}{60}$+4)×300=11s+2 700,y₂=8s+1 000+($\frac{s}{50}$+2)×300=14s+1 600,y₃=10s+700+($\frac{s}{100}$+3)×300=13s+1 600.现在要选择总费用最少的公司,关键是比较y₁,y₂,y₃的大小.因为s>0,所以y₂>y₃恒成立,所以只需比较y₁和y₃的大小.当y₁>y₃时,11s+2 700>13s+1 600,解得s<550.故当两市距离小于550千米时,选择丙公司较好;当y₁=y₃时,s=550.故当两市距离等于550千米时,选择甲或丙公司都一样;当y₁<y₃时,s>550.故当两市的距离大于550千米时,选择甲公司较好.
(1)设A,B两市的距离为x千米,则三家运输公司包装与装卸及运输的费用分别是甲公司(6x+1 500)元,乙公司(8x+1 000)元,丙公司(10x+700)元,依题意,得(8x+1 000)+(10x+700)=2×(6x+1 500),解得x=216$\frac{2}{3}$≈217.故A,B两市的距离约为217千米.
(2)设选择甲、乙、丙三家运输公司的总费用分别为y₁元、y₂元、y₃元,由于三家运输公司包装与装卸及运输所需的时间分别为甲公司($\frac{s}{60}$+4)小时,乙公司($\frac{s}{50}$+2)小时,丙公司($\frac{s}{100}$+3)小时,所以y₁=6s+1 500+($\frac{s}{60}$+4)×300=11s+2 700,y₂=8s+1 000+($\frac{s}{50}$+2)×300=14s+1 600,y₃=10s+700+($\frac{s}{100}$+3)×300=13s+1 600.现在要选择总费用最少的公司,关键是比较y₁,y₂,y₃的大小.因为s>0,所以y₂>y₃恒成立,所以只需比较y₁和y₃的大小.当y₁>y₃时,11s+2 700>13s+1 600,解得s<550.故当两市距离小于550千米时,选择丙公司较好;当y₁=y₃时,s=550.故当两市距离等于550千米时,选择甲或丙公司都一样;当y₁<y₃时,s>550.故当两市的距离大于550千米时,选择甲公司较好.