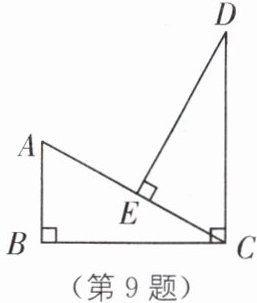
9.(2024·徐州期末)如图,在 Rt△ABC 中,∠B= 90°,BC⊥CD,DE⊥AC 于点 E,AB= CE,求证：△ABC≌△CED.
答案：
∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°.
∵BC⊥CD,
∴∠BCD=90°,
∴∠B+∠BCD=180°,
∴CD//AB,
∴∠A=∠DCE.在△ABC 和△CED 中,{∠A=∠DCE,AB=CE,∠B=∠DEC,}
∴△ABC≌△CED(ASA).归纳总结 本题主要考查全等三角形的判定、垂直的定义和平行线的判定与性质,熟知全等三角形的判定定理是解题基础.
∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°.
∵BC⊥CD,
∴∠BCD=90°,
∴∠B+∠BCD=180°,
∴CD//AB,
∴∠A=∠DCE.在△ABC 和△CED 中,{∠A=∠DCE,AB=CE,∠B=∠DEC,}
∴△ABC≌△CED(ASA).归纳总结 本题主要考查全等三角形的判定、垂直的定义和平行线的判定与性质,熟知全等三角形的判定定理是解题基础.
10. 如图,已知点 D 是△ABC 的边 AB 上一点,DF 交 AC 于点 E,DE= FE,FC//AB. 求证：AD= CF.
答案：
∵FC//AB,
∴∠F=∠ADE.在△ADE 和△CFE 中,{∠ADE=∠F,DE=FE,∠AED=∠CEF,}
∴△ADE≌△CFE(ASA),
∴AD=CF.
∵FC//AB,
∴∠F=∠ADE.在△ADE 和△CFE 中,{∠ADE=∠F,DE=FE,∠AED=∠CEF,}
∴△ADE≌△CFE(ASA),
∴AD=CF.
11.(实验班原创)如图,在△ABC 中,AD 是 BC 边上的中线,E,F 为直线 AD 上的点,连接 BE,CF,且 BE//CF.
(1)求证：△BDE≌△CDF；
(2)若 AE= 15,AF= 6,试求 DE 的长.
(1)求证：△BDE≌△CDF；
(2)若 AE= 15,AF= 6,试求 DE 的长.
答案：
(1)
∵AD 是 BC 边上的中线,
∴BD=CD.
∵BE//CF,
∴∠DBE=∠DCF.在△BDE 和△CDF 中,{∠DBE=∠DCF,BD=CD,∠BDE=∠CDF,}
∴△BDE≌△CDF(ASA).
(2)
∵AE=15,AF=6,
∴EF=AE-AF=15-6=9.
∵△BDE≌△CDF,
∴DE=DF.
∵DE+DF=EF=9,
∴DE=$\frac{9}{2}$.
(1)
∵AD 是 BC 边上的中线,
∴BD=CD.
∵BE//CF,
∴∠DBE=∠DCF.在△BDE 和△CDF 中,{∠DBE=∠DCF,BD=CD,∠BDE=∠CDF,}
∴△BDE≌△CDF(ASA).
(2)
∵AE=15,AF=6,
∴EF=AE-AF=15-6=9.
∵△BDE≌△CDF,
∴DE=DF.
∵DE+DF=EF=9,
∴DE=$\frac{9}{2}$.
12.(中考新考法 动点问题)如图,AE,BD 相交于点 C,AC= EC,BC= DC,AB= 4 cm,点 P 从点 A 出发,沿 A→B→A 方向以 3 cm/s 的速度匀速运动,点 Q 从点 D 出发,沿 D→E 方向以 1 cm/s 的速度匀速运动. P,Q 两点同时出发,当点 P 回到点 A 时,P,Q 两点同时停止运动. 设点 P 的运动时间为 t(s).
(1)当 t= 1 时,AP= ______cm；当 t= 2 时,AP= ______cm；
(2)求证：AB//DE；
(3)连接 PQ,当线段 PQ 经过点 C 时,DQ 的长为______cm.
(1)当 t= 1 时,AP= ______cm；当 t= 2 时,AP= ______cm；
(2)求证：AB//DE；
(3)连接 PQ,当线段 PQ 经过点 C 时,DQ 的长为______cm.
答案：
(1)3 2 ［解析］当 t=1 时,AP=3 cm；当 t=2 时,AP=4-(6 - 4)=2(cm).
(2)在△ABC 和△EDC 中,{AC=EC,∠ACB=∠ECD,BC=DC,}
∴△ABC≌△EDC(SAS),
∴∠A=∠E,
∴AB//DE.
(3)1或2 ［解析］如图,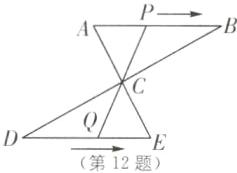
根据题意,得 DQ=t cm,则 EQ=(4 - t)cm,由
(1),得∠A=∠E,ED=AB=4 cm,在△ACP 和△ECQ 中,{∠A=∠E,AC=EC,∠ACP=∠ECQ,}
∴△ACP≌△ECQ(ASA),
∴AP=EQ.当 0≤t≤$\frac{4}{3}$时,3t=4 - t,解得 t=1；当$\frac{4}{3}$＜t≤$\frac{8}{3}$时,8 - 3t=4 - t,解得 t=2.综上所述,当线段 PQ 经过点 C 时,t 的值为 1 或 2,
∴DQ 的长为 1 cm 或 2 cm.
(1)3 2 ［解析］当 t=1 时,AP=3 cm；当 t=2 时,AP=4-(6 - 4)=2(cm).
(2)在△ABC 和△EDC 中,{AC=EC,∠ACB=∠ECD,BC=DC,}
∴△ABC≌△EDC(SAS),
∴∠A=∠E,
∴AB//DE.
(3)1或2 ［解析］如图,
根据题意,得 DQ=t cm,则 EQ=(4 - t)cm,由(1),得∠A=∠E,ED=AB=4 cm,在△ACP 和△ECQ 中,{∠A=∠E,AC=EC,∠ACP=∠ECQ,}
∴△ACP≌△ECQ(ASA),
∴AP=EQ.当 0≤t≤$\frac{4}{3}$时,3t=4 - t,解得 t=1；当$\frac{4}{3}$＜t≤$\frac{8}{3}$时,8 - 3t=4 - t,解得 t=2.综上所述,当线段 PQ 经过点 C 时,t 的值为 1 或 2,
∴DQ 的长为 1 cm 或 2 cm.
13.(2024·吉林中考)如图,在□ABCD 中,点 O 是 AB 的中点,连接 CO 并延长,交 DA 的延长线于点 E. 求证：AE= BC.
答案：
∵点 O 是 AB 的中点,
∴AO=OB.
∵四边形 ABCD 是平行四边形,
∴AD//BC,
∴∠B=∠EAO.又∠AOE=∠BOC,
∴△AOE≌△BOC(ASA),
∴AE=BC.
∵点 O 是 AB 的中点,
∴AO=OB.
∵四边形 ABCD 是平行四边形,
∴AD//BC,
∴∠B=∠EAO.又∠AOE=∠BOC,
∴△AOE≌△BOC(ASA),
∴AE=BC.