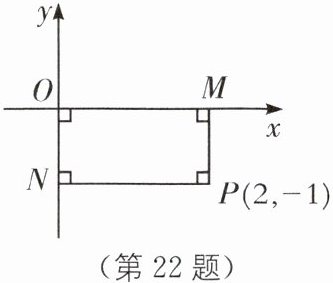
22. (2025·南京建邺区期末)在平面直角坐标系中,点O为坐标原点,点P(x,y)(xy≠0)是平面内任意一点.过点P分别作x轴,y轴的垂线,垂足分别为点M和点N.若四边形PMON的周长为6,则点P叫作“周六点”.例如：如图所示的P(2,-1)是一个“周六点”.
(1)若D(m,2m+2)为“周六点”,求m的值；
(2)点Q的坐标为(2,2),若点P是“周六点”,则PQ的最小值为______.
A. $\frac{\sqrt{2}}{2}$
B. 1
C. $\sqrt{2}$
D. 2
(3)若一次函数y= kx+k-4的图象上存在“周六点”,则k的取值范围是______.
(1)若D(m,2m+2)为“周六点”,求m的值；
(2)点Q的坐标为(2,2),若点P是“周六点”,则PQ的最小值为______.
A. $\frac{\sqrt{2}}{2}$
B. 1
C. $\sqrt{2}$
D. 2
(3)若一次函数y= kx+k-4的图象上存在“周六点”,则k的取值范围是______.
答案：
(1)解法一:①当点D在第一象限时，m+2m+2=3，解得m=1/3；②当点D在第二象限时，-m+2m+2=3，解得m=1(舍去)；③当点D在第三象限时，-m+(-2m-2)=3，解得m=-5/3；④当点D在第四象限时，m+(-2m-2)=3，解得m=-5(舍去).综上所述，m=-5/3或1/3.解法二:由题意，得|m|+|2m+2|=3.①当m≤-1时，-m+(-2m-2)=3，解得m=-5/3；②当-1＜m≤0时，-m+2m+2=3，解得m=1(舍去)；③当m＞0时，m+2m+2=3，解得m=1/3.综上所述，m=-5/3或1/3.解法三:由图
(1)可得点D在第一象限或第三象限.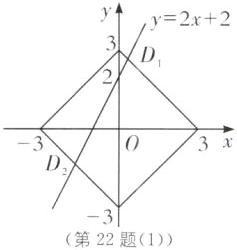
①当点D在第一象限时，2m+2=-m+3，解得m=1/3.②当点D在第三象限时，2m+2=-m-3，解得m=-5/3.综上所述，m=-5/3或1/3.
(2)A [解析]
∵点P是“周六点”，
∴|x|+|y|=3.①当x＜0，y＞0时，y=x+3.如图
(2)，过点Q(2,2)作直线y=x+3的垂线，垂足为H，过点O作OK⊥直线y=x+3于点K.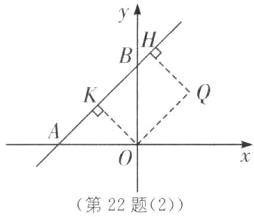
∵OA=OB=3，
∴AB=3√2.
∵OK⊥AB，
∴OK=1/2AB=3√2/2.
∵点P是直线y=x+3上的动点，
∴QH是PQ的最小值.
∵Q(2,2)，
∴OQ的表达式为y=x，
∴OQ//AB，则QH=OK=3√2/2，
∴此时PQ的最小值为3√2/2.②当x＞0，y＞0时，则y=-x+3.如图
(3)，过点Q作QH⊥AB于点H，过点Q作QD⊥y轴于点D，作QE⊥x轴于点E，
则D(0,2)，E(2,0)，F(1,2)，G(2,1)，
∴△QFG是等腰直角三角形，QF=QG=1，
∴QH=√2/2.
∴此时PQ的最小值为√2/2.③当x＜0，y＜0时，则y=-x-3.如图
(4)，同理可得PQ的最小值为7√2/2.
当x＞0，y＜0时，则y=x-3.如图
(5)，同理可得PQ的最小值为3√2/2.
综上所述，PQ的最小值为√2/2.故选A.
(3)k≥1或k＜-2 [解析]由
(2)知当点P(x,y)(xy≠0)是“周六点”时，点P的图象如图
(6)所示:
∵直线y=kx+k-4=k(x+1)-4，当x=-1时，y=-4，
∴直线y=kx+k-4始终经过点P(-1,-4).当k＞0时，则k-4≥-3，
∴k≥1；当k＜0时，则-3k+k-4＞0，
∴k＜-2.综上所述，k的取值范围为k≥1或k＜-2.
(1)解法一:①当点D在第一象限时，m+2m+2=3，解得m=1/3；②当点D在第二象限时，-m+2m+2=3，解得m=1(舍去)；③当点D在第三象限时，-m+(-2m-2)=3，解得m=-5/3；④当点D在第四象限时，m+(-2m-2)=3，解得m=-5(舍去).综上所述，m=-5/3或1/3.解法二:由题意，得|m|+|2m+2|=3.①当m≤-1时，-m+(-2m-2)=3，解得m=-5/3；②当-1＜m≤0时，-m+2m+2=3，解得m=1(舍去)；③当m＞0时，m+2m+2=3，解得m=1/3.综上所述，m=-5/3或1/3.解法三:由图
(1)可得点D在第一象限或第三象限.
①当点D在第一象限时，2m+2=-m+3，解得m=1/3.②当点D在第三象限时，2m+2=-m-3，解得m=-5/3.综上所述，m=-5/3或1/3.(2)A [解析]
∵点P是“周六点”，
∴|x|+|y|=3.①当x＜0，y＞0时，y=x+3.如图
(2)，过点Q(2,2)作直线y=x+3的垂线，垂足为H，过点O作OK⊥直线y=x+3于点K.
∵OA=OB=3，
∴AB=3√2.
∵OK⊥AB，
∴OK=1/2AB=3√2/2.
∵点P是直线y=x+3上的动点，
∴QH是PQ的最小值.
∵Q(2,2)，
∴OQ的表达式为y=x，
∴OQ//AB，则QH=OK=3√2/2，
∴此时PQ的最小值为3√2/2.②当x＞0，y＞0时，则y=-x+3.如图
(3)，过点Q作QH⊥AB于点H，过点Q作QD⊥y轴于点D，作QE⊥x轴于点E，
则D(0,2)，E(2,0)，F(1,2)，G(2,1)，∴△QFG是等腰直角三角形，QF=QG=1，
∴QH=√2/2.
∴此时PQ的最小值为√2/2.③当x＜0，y＜0时，则y=-x-3.如图
(4)，同理可得PQ的最小值为7√2/2.
当x＞0，y＜0时，则y=x-3.如图(5)，同理可得PQ的最小值为3√2/2.
综上所述，PQ的最小值为√2/2.故选A.(3)k≥1或k＜-2 [解析]由
(2)知当点P(x,y)(xy≠0)是“周六点”时，点P的图象如图
(6)所示:
∵直线y=kx+k-4=k(x+1)-4，当x=-1时，y=-4，
∴直线y=kx+k-4始终经过点P(-1,-4).当k＞0时，则k-4≥-3，
∴k≥1；当k＜0时，则-3k+k-4＞0，
∴k＜-2.综上所述，k的取值范围为k≥1或k＜-2.
23. 对于平面直角坐标系xOy中的点A(x,y),给出如下定义,若存在点B(x±a,y±a)(a为正数),称点B为点A的等距点.例如：如图,对于点A(1,1),存在点B(3,3),点C(-1,3),则点B,C分别为点A的等距点.
(1)若点A的坐标是(0,1),写出当a= 4时,点A在第一象限的等距点坐标；
(2)若点A的等距点B的坐标是(-3,1),求当点A的横、纵坐标相同时的坐标；
(3)当将某个点A(x,y)的所有等距点用线段依次连接起来所得到的图形周长不大于$\frac{25}{4}$时,求a的取值范围.
(1)若点A的坐标是(0,1),写出当a= 4时,点A在第一象限的等距点坐标；
(2)若点A的等距点B的坐标是(-3,1),求当点A的横、纵坐标相同时的坐标；
(3)当将某个点A(x,y)的所有等距点用线段依次连接起来所得到的图形周长不大于$\frac{25}{4}$时,求a的取值范围.
答案：
(1)
∵点A的坐标是(0,1)，
∴点A的等距点为(0+4,1+4)，(0+4,1-4)，(0-4,1+4)，(0-4,1-4)，即(4,5)，(4,-3)，(-4,5)，(-4,-3)，
∴当a=4时，点A在第一象限的等距点坐标为(4,5).
(2)由题意，得-3+a=1-a或-3-a=1+a，解得a=2或a=-2.
∵a是正数，
∴a=2.故当点A的横、纵坐标相同时的坐标为(-1,-1).
(3)点A(x,y)的所有等距点的坐标分别为(x+a,y+a)，(x+a,y-a)，(x-a,y+a)，(x-a,y-a)，则所有等距点用线段依次连接起来所得到的图形周长为|8a|，由题意，得|8a|≤25/4，解得0＜a≤25/32.
(1)
∵点A的坐标是(0,1)，
∴点A的等距点为(0+4,1+4)，(0+4,1-4)，(0-4,1+4)，(0-4,1-4)，即(4,5)，(4,-3)，(-4,5)，(-4,-3)，
∴当a=4时，点A在第一象限的等距点坐标为(4,5).
(2)由题意，得-3+a=1-a或-3-a=1+a，解得a=2或a=-2.
∵a是正数，
∴a=2.故当点A的横、纵坐标相同时的坐标为(-1,-1).
(3)点A(x,y)的所有等距点的坐标分别为(x+a,y+a)，(x+a,y-a)，(x-a,y+a)，(x-a,y-a)，则所有等距点用线段依次连接起来所得到的图形周长为|8a|，由题意，得|8a|≤25/4，解得0＜a≤25/32.
24. 中考新考法 长方形中的动点问题 如图(1),以长方形ABCD的中心O为原点,平行于BC的直线为x轴,平行于AB的直线为y轴建立平面直角坐标系,若点D的坐标为(6,3).
(1)直接写出点A,B,C的坐标.
(2)设AD的中点为E,点M是y轴上的点,且△CME的面积是长方形ABCD面积的$\frac{1}{6}$,求点M的坐标.
(3)如图(2),若点P从点C出发向CB方向匀速移动(不超过点B),点Q从点B出发向BA方向匀速移动(不超过点A),且点Q的速度是点P的一半,P,Q两点同时出发,已知当移动时间为t秒时,点P的横坐标为6-2t,此时①CP= ______
②在点P,Q移动的过程中,四边形PBQD的面积是否发生变化？若不变,求其值；若变化,求其变化范围.
(1)直接写出点A,B,C的坐标.
(2)设AD的中点为E,点M是y轴上的点,且△CME的面积是长方形ABCD面积的$\frac{1}{6}$,求点M的坐标.
(3)如图(2),若点P从点C出发向CB方向匀速移动(不超过点B),点Q从点B出发向BA方向匀速移动(不超过点A),且点Q的速度是点P的一半,P,Q两点同时出发,已知当移动时间为t秒时,点P的横坐标为6-2t,此时①CP= ______
2t
,AQ= ______6-t
(用含t的式子表示).②在点P,Q移动的过程中,四边形PBQD的面积是否发生变化？若不变,求其值；若变化,求其变化范围.
不变.理由如下:∵四边形PBQD的面积=12×6-1/2(6-t)×12-1/2×2t×6=36,∴四边形PBQD的面积不发生变化，面积为36.
答案：
(1)点A，B，C的坐标分别为(-6,3)，(-6,-3)，(6,-3).
(2)由题意，得点E的坐标为(0,3)，设点M的坐标为(0,a)，则1/2×|a-3|×6=1/6×12×6，解得a=-1或a=7，
∴点M的坐标为(0,-1)或(0,7).
(3)①2t 6-t ②不变.理由如下:
∵四边形PBQD的面积=12×6-1/2(6-t)×12-1/2×2t×6=36，
∴四边形PBQD的面积不发生变化，面积为36.
(1)点A，B，C的坐标分别为(-6,3)，(-6,-3)，(6,-3).
(2)由题意，得点E的坐标为(0,3)，设点M的坐标为(0,a)，则1/2×|a-3|×6=1/6×12×6，解得a=-1或a=7，
∴点M的坐标为(0,-1)或(0,7).
(3)①2t 6-t ②不变.理由如下:
∵四边形PBQD的面积=12×6-1/2(6-t)×12-1/2×2t×6=36，
∴四边形PBQD的面积不发生变化，面积为36.