1. 某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了$\frac{1}{5}$,如果加满汽油后汽车行驶的路程为$x$ km,油箱中剩油量为$y$ L,则$y与x$之间的函数表达式和自变量取值范围分别是(
A.$y= 0.12x,x>0$
B.$y= 60-0.12x,x>0$
C.$y= 0.12x,0\leqslant x\leqslant 500$
D.$y= 60-0.12x,0\leqslant x\leqslant 500$
D
).A.$y= 0.12x,x>0$
B.$y= 60-0.12x,x>0$
C.$y= 0.12x,0\leqslant x\leqslant 500$
D.$y= 60-0.12x,0\leqslant x\leqslant 500$
答案:D [解析]由油箱容量为60L的汽车,加满汽油后行驶了100km时,油箱中的汽油大约消耗了$\frac{1}{5}$,得$\frac{1}{5}$×60÷100 = 0.12(L/km),60÷0.12 = 500(km),所以y与x之间的函数表达式和自变量取值范围为y = 60 - 0.12x(0≤x≤500)。故选D。
易错警示 本题主要考查了一次函数的实际应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义。
易错警示 本题主要考查了一次函数的实际应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义。
2. (2024·青海中考)如图,一次函数$y= 2x-3的图象与x轴相交于点A$,则点$A关于y$轴的对称点是(
A.$(-\frac{3}{2},0)$
B.$(\frac{3}{2},0)$
C.$(0,3)$
D.$(0,-3)$
A
).A.$(-\frac{3}{2},0)$
B.$(\frac{3}{2},0)$
C.$(0,3)$
D.$(0,-3)$
答案:A [解析]对于一次函数y = 2x - 3,令y = 0,可得x = $\frac{3}{2}$,
∴A($\frac{3}{2}$,0),
∴点A关于y轴的对称点的坐标为(-$\frac{3}{2}$,0)。故选A。
∴A($\frac{3}{2}$,0),
∴点A关于y轴的对称点的坐标为(-$\frac{3}{2}$,0)。故选A。
3. (2024·常州中考)在马拉松、公路自行车等耐力运动的训练或比赛中,为合理分配体能,运动员通常会记录每行进1 km所用的时间,即“配速”(单位:min/km).小华参加5 km的骑行比赛,他骑行的“配速”如图所示,则下列说法中错误的是(
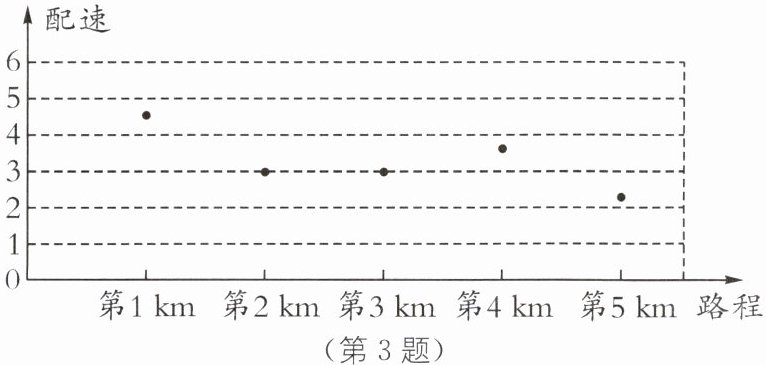
A.第1 km所用的时间最长
B.第5 km的平均速度最大
C.第2 km和第3 km的平均速度相同
D.前2 km的平均速度大于最后2 km的平均速度
D
).
A.第1 km所用的时间最长
B.第5 km的平均速度最大
C.第2 km和第3 km的平均速度相同
D.前2 km的平均速度大于最后2 km的平均速度
答案:D [解析]由图象可知,第1km所用的时间最长,约4.5分钟。故选项A说法正确,不符合题意;第5km所用的时间最短,即平均速度最大。故选项B说法正确,不符合题意;第2km和第3km的平均速度相同。故选项C说法正确,不符合题意;前2km的平均速度小于最后2km的平均速度。故选项D说法错误,符合题意。故选D。
归纳总结 本题考查函数的图象,掌握时间、速度、路程之间的数量关系是解题的关键。
归纳总结 本题考查函数的图象,掌握时间、速度、路程之间的数量关系是解题的关键。
4. 如图反映的过程是小刚从家去菜地浇水,又去青稞地除草,然后回家,如果菜地和青稞地的距离为$a$ km,小刚在青稞地除草比在菜地浇水多用了$b$ min,则$a,b$的值分别为(

A.1,8
B.0.5,12
C.1,12
D.0.5,8
D
).
A.1,8
B.0.5,12
C.1,12
D.0.5,8
答案:D [解析]此函数图象大致可分以下几个阶段:
①0~12分钟,小刚从家走到菜地;
②12~27分钟,小刚在菜地浇水;
③27~33分钟,小刚从菜地走到青稞地;
④33~56分钟,小刚在青稞地除草;
⑤56~74分钟,小刚从青稞地回到家。
综合上面的分析,由③的过程可知,a = 1.5 - 1 = 0.5;
由②④的过程知,b = (56 - 33) - (27 - 12) = 8。故选D。
方法诠释 本题主要考查了函数图象的读图能力和函数与实际问题结合的应用,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,并结合实际意义得到正确的结论。
①0~12分钟,小刚从家走到菜地;
②12~27分钟,小刚在菜地浇水;
③27~33分钟,小刚从菜地走到青稞地;
④33~56分钟,小刚在青稞地除草;
⑤56~74分钟,小刚从青稞地回到家。
综合上面的分析,由③的过程可知,a = 1.5 - 1 = 0.5;
由②④的过程知,b = (56 - 33) - (27 - 12) = 8。故选D。
方法诠释 本题主要考查了函数图象的读图能力和函数与实际问题结合的应用,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,并结合实际意义得到正确的结论。
5. 将一次函数$y= x$的图象向上平移2个单位长度,平移后,若$y>0$,则$x$的取值范围是(
A.$x>4$
B.$x>-4$
C.$x>2$
D.$x>-2$
D
).A.$x>4$
B.$x>-4$
C.$x>2$
D.$x>-2$
答案:D [解析]
∵将一次函数y = x的图象向上平移2个单位长度,
∴平移后的表达式为y = x + 2。当y>0时,x> - 2,
∴x的取值范围是x> - 2。故选D
∵将一次函数y = x的图象向上平移2个单位长度,
∴平移后的表达式为y = x + 2。当y>0时,x> - 2,
∴x的取值范围是x> - 2。故选D
6. (2024·哈尔滨中考)一个有进水管与出水管的容器,从某时刻开始5 min内只进水不出水,在随后的10 min内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的水量$y$(单位:L)与时间$x$(单位:min)之间的关系如图所示,当$x= 9$ min时,$y= $
A.36 L
B.38 L
C.40 L
D.42 L
B
.A.36 L
B.38 L
C.40 L
D.42 L
答案:B [解析]设当5≤x≤15时,y与x的函数表达式为y = kx + b(k≠0)。
∵图象过(5,30),(15,50),
∴$\begin{cases}5k + b = 30\\15k + b = 50\end{cases}$,解得$\begin{cases}k = 2\\b = 20\end{cases}$,
∴y = 2x + 20。
令x = 9,
∴y = 2×9 + 20 = 38。故选B
∵图象过(5,30),(15,50),
∴$\begin{cases}5k + b = 30\\15k + b = 50\end{cases}$,解得$\begin{cases}k = 2\\b = 20\end{cases}$,
∴y = 2x + 20。
令x = 9,
∴y = 2×9 + 20 = 38。故选B