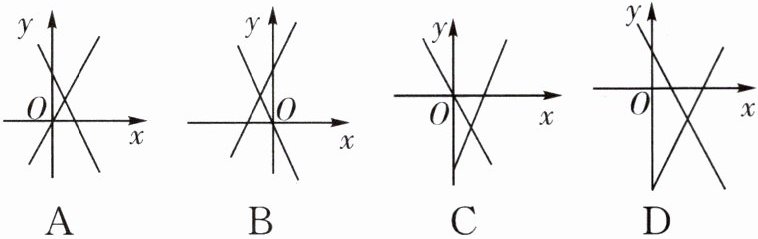
7. 在同一平面直角坐标系中,函数$y= -mx(m\neq 0)与y= 2x+m$的图象大致是(
 A B C D
A B C D
B
). A B C D
A B C D答案:B [解析]当m>0时, - m<0,函数y = - mx(m≠0)的图象过原点且经过第二、四象限,y = 2x + m的图象经过第一、二、三象限,选项B符合;
当m<0时, - m>0,函数y = - mx(m≠0)的图象过原点且经过第一、三象限,y = 2x + m的图象经过第一、三、四象限,没有符合选项。故选B。
关键提醒 本题考查了正比例函数及一次函数的图象,解题的关键是了解这两种函数的性质。
当m<0时, - m>0,函数y = - mx(m≠0)的图象过原点且经过第一、三象限,y = 2x + m的图象经过第一、三、四象限,没有符合选项。故选B。
关键提醒 本题考查了正比例函数及一次函数的图象,解题的关键是了解这两种函数的性质。
8. 若直线$l_1经过点(0,4)$,$l_2经过点(3,2)$,且$l_1与l_2$关于x轴对称,则$l_1与l_2$的交点坐标为(
A.$(-2,0)$
B.$(2,0)$
C.$(-6,0)$
D.$(6,0)$
B
).A.$(-2,0)$
B.$(2,0)$
C.$(-6,0)$
D.$(6,0)$
答案:B [解析]
∵直线$l_1$经过点(0,4),$l_2$经过点(3,2),且$l_1$与$l_2$关于x轴对称,
∴两直线相交于x轴上,直线$l_1$经过点(3,-2),$l_2$经过点(0,-4)。
设直线$l_1$的表达式为y = kx + b,把(0,4)和(3,-2)代入,得$\begin{cases}b = 4\\3k + b = - 2\end{cases}$,解得$\begin{cases}k = - 2\\b = 4\end{cases}$,
∴直线$l_1$的表达式为y = - 2x + 4。
令y = 0,则 - 2x + 4 = 0,解得x = 2,即$l_1$与$l_2$的交点坐标为(2,0)。故选B
∵直线$l_1$经过点(0,4),$l_2$经过点(3,2),且$l_1$与$l_2$关于x轴对称,
∴两直线相交于x轴上,直线$l_1$经过点(3,-2),$l_2$经过点(0,-4)。
设直线$l_1$的表达式为y = kx + b,把(0,4)和(3,-2)代入,得$\begin{cases}b = 4\\3k + b = - 2\end{cases}$,解得$\begin{cases}k = - 2\\b = 4\end{cases}$,
∴直线$l_1$的表达式为y = - 2x + 4。
令y = 0,则 - 2x + 4 = 0,解得x = 2,即$l_1$与$l_2$的交点坐标为(2,0)。故选B
9. (2024·大庆中考)写出一个过点$(1,1)且y的值随着x$值增大而减小的函数表达式:______
y = - x + 2(答案不唯一)
.答案:y = - x + 2(答案不唯一) [解析]由题意,可令这个函数的表达式为y = - x + b,
将点(1,1)代入函数表达式,得b = 2,
所以函数表达式为y = - x + 2。
归纳总结 本题主要考查了一次函数的性质:当k>0时,y随x的增大而增大,函数图象从左到右呈上升趋势;当k<0时,y随x的增大而减小,函数图象从左到右呈下降趋势。
将点(1,1)代入函数表达式,得b = 2,
所以函数表达式为y = - x + 2。
归纳总结 本题主要考查了一次函数的性质:当k>0时,y随x的增大而增大,函数图象从左到右呈上升趋势;当k<0时,y随x的增大而减小,函数图象从左到右呈下降趋势。
10. (2024·镇江中考)点$A(1,y_1)$,$B(2,y_2)在一次函数y= 3x+1$的图象上,则$y_1$
<
$y_2$(用“<”“=”或“>”填空).答案:< [解析]
∵k = 3>0,
∴y随x的增大而增大。
又点A(1,$y_1$),B(2,$y_2$)在一次函数y = 3x + 1的图象上,且1<2,
∴$y_1$<$y_2$。
∵k = 3>0,
∴y随x的增大而增大。
又点A(1,$y_1$),B(2,$y_2$)在一次函数y = 3x + 1的图象上,且1<2,
∴$y_1$<$y_2$。
11. (2024·黑龙江中考)在函数$y= \frac{\sqrt{x-3}}{x+2}$中,自变量$x$的取值范围是
x≥3
.答案:x≥3 [解析]由题意,得x - 3≥0且x + 2≠0,
解得x≥3。
解得x≥3。
12. 中考新考法 满足结论的条件开放 如图,在平面直角坐标系中,点$A,B的坐标分别为(1,3)$,$(n,3)$,若直线$y= 2x与线段AB$有公共点,则$n$的值可以为______.(写出一个即可)


2
答案:2(答案不唯一) [解析]
∵直线y = 2x与线段AB有公共点,
∴2n≥3,
∴n≥$\frac{3}{2}$,
∴n = 2符合题意。
归纳总结 本题考查了一次函数图象上点的坐标特征,用一次函数图象上点的坐标特征,找出关于n的一元一次不等式是解题的关键。
∵直线y = 2x与线段AB有公共点,
∴2n≥3,
∴n≥$\frac{3}{2}$,
∴n = 2符合题意。
归纳总结 本题考查了一次函数图象上点的坐标特征,用一次函数图象上点的坐标特征,找出关于n的一元一次不等式是解题的关键。
13. 如图,三角形$ABC的高AD= 4$,$BC= 6$,点$E在BC$上运动,若设$BE的长为x$,三角形$ACE的面积为y$,则$y关于x$的函数表达式为______.


y = - 2x + 12
答案:y = - 2x + 12 [解析]
∵BC = 6,BE = x,
∴CE = 6 - x,
∴y = $\frac{1}{2}$×4×(6 - x) = - 2x + 12。
∵BC = 6,BE = x,
∴CE = 6 - x,
∴y = $\frac{1}{2}$×4×(6 - x) = - 2x + 12。
14. 如图,直线$y= -x+m与y= nx+4n(n\neq 0)的交点的横坐标为-2$,则关于$x的不等式-x+m>nx+4n>0$的整数解是______.


-3
答案:- 3 [解析]
∵直线y = - x + m与y = nx + 4n的交点的横坐标为 - 2,
∴关于x的不等式 - x + m>nx + 4n的解集为x< - 2。
∵当y = nx + 4n = 0时,x = - 4,
∴nx + 4n>0的解集为x> - 4。
∴ - x + m>nx + 4n>0的解集为 - 4<x< - 2。
∴整数解是 - 3。
∵直线y = - x + m与y = nx + 4n的交点的横坐标为 - 2,
∴关于x的不等式 - x + m>nx + 4n的解集为x< - 2。
∵当y = nx + 4n = 0时,x = - 4,
∴nx + 4n>0的解集为x> - 4。
∴ - x + m>nx + 4n>0的解集为 - 4<x< - 2。
∴整数解是 - 3。
15. (2024·潍坊中考)请写出同时满足以下两个条件的一个函数
y = - x + 2(答案不唯一)
.①$y随着x$的增大而减小;②函数图象与$y$轴正半轴相交.答案:y = - x + 2(答案不唯一) [解析]
∵y随着x的增大而减小,
∴一次函数的比例系数k<0,
又函数图象与y轴正半轴相交,
∴b>0,
∴同时满足题中两个条件的一次函数可以是y = - x + 2。
∵y随着x的增大而减小,
∴一次函数的比例系数k<0,
又函数图象与y轴正半轴相交,
∴b>0,
∴同时满足题中两个条件的一次函数可以是y = - x + 2。
16. 如图(1),在长方形$ABCD$中,动点$P从点B$出发,沿$BC,CD,DA运动至点A$停止,设点$P运动的路程为x$,$\triangle ABP的面积为y$,如果$y关于x$的函数图象如图(2)所示,那么$\triangle ABC$的周长是______

8 + $\sqrt{34}$
.
答案:8 + $\sqrt{34}$ [解析]由题意可知,动点P从点B出发,沿BC,CD,DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变。
函数图象上横轴表示点P运动的路程,当x = 3时,y开始不变,说明BC = 3;当x = 8时,y接着变化,说明CD = 8 - 3 = 5,
∴AB = 5,BC = 3。
∴AC = $\sqrt{AB^{2}+BC^{2}}$ = $\sqrt{34}$
∴△ABC的周长是AB + BC + AC = 8 + $\sqrt{34}$
归纳总结 本题主要考查了动点问题的函数图象,根据函数的图象求出线段的长度从而得出三角形的周长是解题的关键。
函数图象上横轴表示点P运动的路程,当x = 3时,y开始不变,说明BC = 3;当x = 8时,y接着变化,说明CD = 8 - 3 = 5,
∴AB = 5,BC = 3。
∴AC = $\sqrt{AB^{2}+BC^{2}}$ = $\sqrt{34}$
∴△ABC的周长是AB + BC + AC = 8 + $\sqrt{34}$
归纳总结 本题主要考查了动点问题的函数图象,根据函数的图象求出线段的长度从而得出三角形的周长是解题的关键。
17. 若一次函数$y= kx+b$($k为常数且k\neq 0$)的图象经过点$(-2,0)$,则关于$x的方程k(x-5)+b= 0$的解为______
3
.答案:x = 3 [解析]
∵直线y = k(x - 5) + b是由直线y = kx + b向右平移5个单位长度所得,y = kx + b与x轴交点为(-2,0),
∴直线y = k(x - 5) + b与x轴交点坐标为(3,0),
∴k(x - 5) + b = 0的解为x = 3。
∵直线y = k(x - 5) + b是由直线y = kx + b向右平移5个单位长度所得,y = kx + b与x轴交点为(-2,0),
∴直线y = k(x - 5) + b与x轴交点坐标为(3,0),
∴k(x - 5) + b = 0的解为x = 3。
18. 如图,在坐标轴上取点$A_1(2,0)$,作$x轴的垂线与直线y= 2x交于点B_1$,作等腰直角三角形$A_1B_1A_2$;又过点$A_2作x轴的垂线与直线y= 2x交于点B_2$,作等腰直角三角形$A_2B_2A_3$;…,如此反复作等腰直角三角形,当作到点$A_n$($n$为正整数)时,则点$A_n$的坐标是______.


(2×$3^{n - 1}$,0)
答案:(2×$3^{n - 1}$,0) [解析]
∵点$B_1$,$B_2$,$B_3$,... ,$B_n$在直线y = 2x的图象上,
∴$A_1B_1$ = 4,$A_2B_2$ = 2×(2 + 4) = 12,
$A_3B_3$ = 2×(2 + 4 + 12) = 36,$A_4B_4$ = 2×(2 + 4 + 12 + 36) = 108,... ,
∴$A_nB_n$ = 4×$3^{n - 1}$(n为正整数)。
∵$OA_n$ = $\frac{1}{2}$$A_nB_n$,
∴点$A_n$的坐标为(2×$3^{n - 1}$,0)。
∵点$B_1$,$B_2$,$B_3$,... ,$B_n$在直线y = 2x的图象上,
∴$A_1B_1$ = 4,$A_2B_2$ = 2×(2 + 4) = 12,
$A_3B_3$ = 2×(2 + 4 + 12) = 36,$A_4B_4$ = 2×(2 + 4 + 12 + 36) = 108,... ,
∴$A_nB_n$ = 4×$3^{n - 1}$(n为正整数)。
∵$OA_n$ = $\frac{1}{2}$$A_nB_n$,
∴点$A_n$的坐标为(2×$3^{n - 1}$,0)。
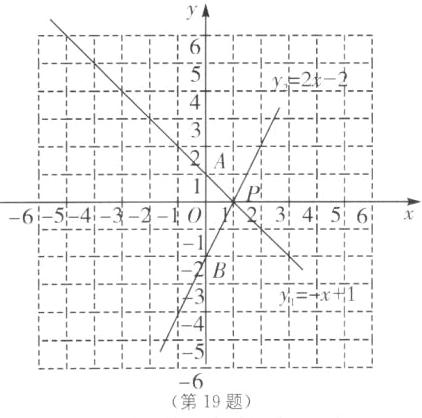
19. 已知直线$y_1= -x+1与直线y_2= 2x-2相交于点P$,它们与$y轴分别交于点A,B$.
(1)在同一平面直角坐标系中画出这两个函数的图象;
(2)观察图象,分别求出当$x$为何值时,$y_1= y_2$,$y_1\geqslant y_2$;
(3)求$\triangle ABP$的面积.

(1)在同一平面直角坐标系中画出这两个函数的图象;
(2)观察图象,分别求出当$x$为何值时,$y_1= y_2$,$y_1\geqslant y_2$;
(3)求$\triangle ABP$的面积.

答案:
(1)
∵当x = 0时,$y_1$ = 1;当$y_1$ = 0时,x = 1,
∴直线$y_1$ = - x + 1经过点(0,1),(1,0)。
同理,直线$y_2$ = 2x - 2经过点(0,-2),(1,0)。
画出$y_1$,$y_2$的图象如图所示:
(2)由
(1)可知这两个函数图象的交点坐标是(1,0)。
由图中的两条直线知,当x = 1时,$y_1$ = $y_2$;当x≤1时,$y_1$≥$y_2$。
(3)
∵A(0,1),P(1,0),B(0,-2),
∴AB = 3,OP = 1,
∴△ABP的面积是$\frac{1}{2}$AB·OP = $\frac{1}{2}$×3×1 = $\frac{3}{2}$。
(1)
∵当x = 0时,$y_1$ = 1;当$y_1$ = 0时,x = 1,
∴直线$y_1$ = - x + 1经过点(0,1),(1,0)。
同理,直线$y_2$ = 2x - 2经过点(0,-2),(1,0)。
画出$y_1$,$y_2$的图象如图所示:

(2)由
(1)可知这两个函数图象的交点坐标是(1,0)。
由图中的两条直线知,当x = 1时,$y_1$ = $y_2$;当x≤1时,$y_1$≥$y_2$。
(3)
∵A(0,1),P(1,0),B(0,-2),
∴AB = 3,OP = 1,
∴△ABP的面积是$\frac{1}{2}$AB·OP = $\frac{1}{2}$×3×1 = $\frac{3}{2}$。