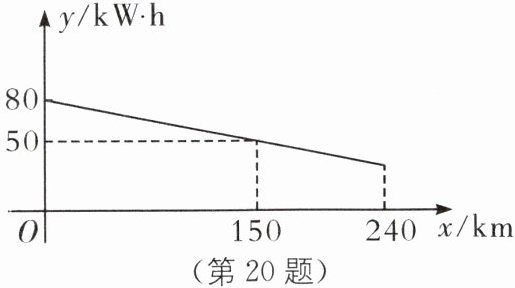
20. (2024·陕西中考)我国新能源汽车快速健康发展,续航里程不断提升,王师傅驾驶一辆纯电动汽车从$A市前往B$市.他驾车从$A$市一高速公路入口驶入时,该车的剩余电量是80 kW·h,行驶了240 km后,从$B$市一高速公路出口驶出.已知该车在高速公路上行驶的过程中,剩余电量$y$(kW·h)与行驶路程$x$(km)之间的关系如图所示.
(1)求$y与x$之间的关系式;
(2)已知这辆车的“满电量”为100 kW·h,求王师傅驾车从$B$市这一高速公路出口驶出时,该车的剩余电量占“满电量”的百分之多少.
(1)求$y与x$之间的关系式;
(2)已知这辆车的“满电量”为100 kW·h,求王师傅驾车从$B$市这一高速公路出口驶出时,该车的剩余电量占“满电量”的百分之多少.

答案:
(1)设y = kx + b(k≠0,0≤x≤240),代入(0,80),(150,50),得$\begin{cases}b = 80\\150k + b = 50\end{cases}$,解得$\begin{cases}k = -\frac{1}{5}\\b = 80\end{cases}$,
∴y与x之间的关系为y = - $\frac{1}{5}$x + 80。
(2)令x = 240,则y = - $\frac{1}{5}$×240 + 80 = 32,$\frac{32}{100}$×100% = 32%。
故该车的剩余电量占“满电量”的32%。
(1)设y = kx + b(k≠0,0≤x≤240),代入(0,80),(150,50),得$\begin{cases}b = 80\\150k + b = 50\end{cases}$,解得$\begin{cases}k = -\frac{1}{5}\\b = 80\end{cases}$,
∴y与x之间的关系为y = - $\frac{1}{5}$x + 80。
(2)令x = 240,则y = - $\frac{1}{5}$×240 + 80 = 32,$\frac{32}{100}$×100% = 32%。
故该车的剩余电量占“满电量”的32%。
21. 如图,点$A(1,0)$,$B(4,0)$,$M(5,3)$.动点$P从点A$出发,沿$x$轴以每秒1个单位长度的速度向右移动,过点$P的直线l:y= -x+b$也随之移动.设移动时间为$t$秒.
(1)当$t= 1$时,求直线$l$的函数表达式;
(2)若直线$l与线段BM$有公共点,求$t$的取值范围.

(1)当$t= 1$时,求直线$l$的函数表达式;
(2)若直线$l与线段BM$有公共点,求$t$的取值范围.

答案:
(1)由题意,得直线y = - x + b交x轴于点P(1 + t,0)(b>0,t≥0)。当t = 1时,1 + t = 2,
∴P(2,0)。
∴ - 2 + b = 0,解得b = 2。
故当t = 1时,直线l的函数表达式为y = - x + 2。
(2)当直线y = - x + b过点B(4,0)时,
有1 + t = 4,
∴t = 3。
当直线y = - x + b过点M(5,3)时,
有3 = - 5 + b,解得b = 8,
∴0 = - (1 + t) + 8,解得t = 7。
故若l与线段BM有公共点,则t的取值范围是3≤t≤7。
(1)由题意,得直线y = - x + b交x轴于点P(1 + t,0)(b>0,t≥0)。当t = 1时,1 + t = 2,
∴P(2,0)。
∴ - 2 + b = 0,解得b = 2。
故当t = 1时,直线l的函数表达式为y = - x + 2。
(2)当直线y = - x + b过点B(4,0)时,
有1 + t = 4,
∴t = 3。
当直线y = - x + b过点M(5,3)时,
有3 = - 5 + b,解得b = 8,
∴0 = - (1 + t) + 8,解得t = 7。
故若l与线段BM有公共点,则t的取值范围是3≤t≤7。
22. (2024·广安中考)某小区物管中心计划采购$A,B$两种花卉用于美化环境.已知购买2株$A$种花卉和3株$B$种花卉共需要21元;购买4株$A$种花卉和5株$B$种花卉共需要37元.
(1)求$A,B$两种花卉的单价.
(2)该物管中心计划采购$A,B$两种花卉共计10000株,其中采购$A种花卉的株数不超过B$种花卉株数的4倍,当$A,B$两种花卉分别采购多少株时,总费用最少?并求出最少总费用.
(1)求$A,B$两种花卉的单价.
(2)该物管中心计划采购$A,B$两种花卉共计10000株,其中采购$A种花卉的株数不超过B$种花卉株数的4倍,当$A,B$两种花卉分别采购多少株时,总费用最少?并求出最少总费用.
答案:
(1)设A种花卉的单价为x元,B种花卉的单价为y元。由题意,得$\begin{cases}2x + 3y = 21\\4x + 5y = 37\end{cases}$,解得$\begin{cases}x = 3\\y = 5\end{cases}$,
故A种花卉的单价为3元,B种花卉的单价为5元。
(2)设总费用为W元,采购A种花卉m株,则采购B种花卉(10000 - m)株。
由题意,得W = 3m + 5(10000 - m) = - 2m + 50000。
∵m≤4(10000 - m),解得m≤8000,
在W = - 2m + 50000中, - 2<0,
∴W随m的增大而减小,
∴当m = 8000时,W的值最小,
W = - 2×8000 + 50000 = 34000,
此时10000 - m = 2000。
故当购进A种花卉8000株,B种花卉2000株时,总费用最少,最少费用为34000元。
(1)设A种花卉的单价为x元,B种花卉的单价为y元。由题意,得$\begin{cases}2x + 3y = 21\\4x + 5y = 37\end{cases}$,解得$\begin{cases}x = 3\\y = 5\end{cases}$,
故A种花卉的单价为3元,B种花卉的单价为5元。
(2)设总费用为W元,采购A种花卉m株,则采购B种花卉(10000 - m)株。
由题意,得W = 3m + 5(10000 - m) = - 2m + 50000。
∵m≤4(10000 - m),解得m≤8000,
在W = - 2m + 50000中, - 2<0,
∴W随m的增大而减小,
∴当m = 8000时,W的值最小,
W = - 2×8000 + 50000 = 34000,
此时10000 - m = 2000。
故当购进A种花卉8000株,B种花卉2000株时,总费用最少,最少费用为34000元。