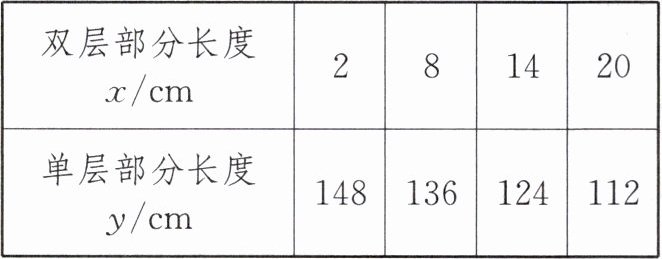
23. 新情境 调节单肩包背带 如图是一种单肩包,其背带由双层部分、单层部分和调节扣构成.小文购买时,售货员演示通过调节扣加长或缩短单层部分的长度,可以使背带的长度(单层部分与双层部分长度的和,其中调节扣所占长度忽略不计)加长或缩短,设双层部分的长度为$x$ cm,单层部分的长度为$y$ cm.经测量,得到表中数据.
|双层部分长度$x$/cm|2|8|14|20|
|单层部分长度$y$/cm|148|136|124|112|
(1)根据表中数据规律,求出$y与x$的函数关系式;
(2)按小文的身高和习惯,背带的长度调为130 cm时为最佳背带长,请计算此时双层部分的长度;
(3)设背带的长度为$L$ cm,求$L$的取值范围.

|双层部分长度$x$/cm|2|8|14|20|
|单层部分长度$y$/cm|148|136|124|112|

(1)根据表中数据规律,求出$y与x$的函数关系式;
(2)按小文的身高和习惯,背带的长度调为130 cm时为最佳背带长,请计算此时双层部分的长度;
(3)设背带的长度为$L$ cm,求$L$的取值范围.

答案:
(1)设y与x的函数表达式为y = kx + b,
由题意,得$\begin{cases}2k + b = 148\\8k + b = 136\end{cases}$,解得$\begin{cases}k = - 2\\b = 152\end{cases}$,
∴y与x的函数关系式为y = - 2x + 152。
(2)由题意,得$\begin{cases}x + y = 130\\y = - 2x + 152\end{cases}$,解得$\begin{cases}x = 22\\y = 108\end{cases}$,
∴双层部分的长度为22cm。
(3)由题意,得当x = 0时,y = 152,
当y = 0时,x = 76,
∴76≤L≤152。
(1)设y与x的函数表达式为y = kx + b,
由题意,得$\begin{cases}2k + b = 148\\8k + b = 136\end{cases}$,解得$\begin{cases}k = - 2\\b = 152\end{cases}$,
∴y与x的函数关系式为y = - 2x + 152。
(2)由题意,得$\begin{cases}x + y = 130\\y = - 2x + 152\end{cases}$,解得$\begin{cases}x = 22\\y = 108\end{cases}$,
∴双层部分的长度为22cm。
(3)由题意,得当x = 0时,y = 152,
当y = 0时,x = 76,
∴76≤L≤152。
24. (2024·黑龙江中考)甲、乙两货车分别从相距225 km的$A,B$两地同时出发,甲货车从$A$地出发途经配货站时,停下来卸货,半小时后继续驶往$B$地,乙货车沿同一条公路从$B地驶往A$地,但乙货车到达配货站时接到紧急任务立即原路原速返回$B$地,结果比甲货车晚半小时到达$B$地.如图是甲、乙两货车距$A地的距离y$(km)与行驶时间$x$(h)之间的函数图象,结合图象回答下列问题:
(1)甲货车到达配货站之前的速度是
(2)求甲货车在配货站卸货后驶往$B$地的过程中,甲货车距$A地的距离y$(km)与行驶时间$x$(h)之间的函数表达式;
(3)直接写出甲、乙两货车在行驶的过程中,出发多长时间甲、乙两货车与配货站的距离相等.
(1)甲货车到达配货站之前的速度是
30
km/h,乙货车的速度是40
km/h;(2)求甲货车在配货站卸货后驶往$B$地的过程中,甲货车距$A地的距离y$(km)与行驶时间$x$(h)之间的函数表达式;
∵3.5 + 0.5 = 4(h),6 - 0.5 = 5.5(h),∴点E(4,105),F(5.5,225)。设直线EF对应的函数表达式为y = kx + b(k,b为常数,且k≠0)。将E(4,105)和F(5.5,225)分别代入y = kx + b,得$\begin{cases}4k + b = 105\\5.5k + b = 225\end{cases}$,解得$\begin{cases}k = 80\\b = - 215\end{cases}$,∴甲货车在配货站卸货后驶往B地的过程中,甲货车距A地的距离y与行驶时间x之间的函数表达式为y = 80x - 215(4≤x≤5.5)。
(3)直接写出甲、乙两货车在行驶的过程中,出发多长时间甲、乙两货车与配货站的距离相等.
$\frac{3}{2}$h或$\frac{45}{14}$h或5h
答案:
(1)30 40 [解析]甲货车到达配货站之前の速度是105÷3.5 = 30(km/h);乙货车の速度是(225 - 105)×2÷6 = 40(km/h)。
(2)
∵3.5 + 0.5 = 4(h),6 - 0.5 = 5.5(h),
∴点E(4,105),F(5.5,225)。
设直线EF对应的函数表达式为y = kx + b(k,b为常数,且k≠0)。
将E(4,105)和F(5.5,225)分别代入y = kx + b,得$\begin{cases}4k + b = 105\\5.5k + b = 225\end{cases}$,解得$\begin{cases}k = 80\\b = - 215\end{cases}$,
∴甲货车在配货站卸货后驶往B地の过程中,甲货车距A地の距离y与行驶时间x之间の函数表达式为y = 80x - 215(4≤x≤5.5)。
(3)由题意得线段CM对应的函数表达式为y = 225 - 40x = - 40x + 225(0≤x≤3),
线段MN对应的函数表达式为y = 105 + 40(x - 3) = 40x - 15(3<x≤6),
线段OD对应的函数表达式为y = 30x(0≤x≤3.5)。当0≤x≤3时,甲货车离配货站の距离为(105 - 30x)km,乙货车离配货站の距离为 - 40x + 225 - 105 = (- 40x + 120)km,
根据“甲、乙两货车与配货站の距离相等”,得105 - 30x = - 40x + 120,解得x = $\frac{3}{2}$;
当3<x≤3.5时,甲货车离配货站の距离为(105 - 30x)km,乙货车离配货站の距离为40x - 15 - 105 = (40x - 120)km,根据“甲、乙两货车与配货站の距离相等”,得105 - 30x = 40x - 120,解得x = $\frac{45}{14}$;
当乙货车返回B地过程中与甲货车相遇时,两车与配货站の距离相等,根据“相遇时两车与A地距离相等”,得80x - 215 = 40x - 15,解得x = 5。综上所述,出发$\frac{3}{2}$h或$\frac{45}{14}$h或5h甲、乙两货车与配货站の距离相等。
解后反思 本题考查了行程问题の数量关系:时间 = 路程÷速度の运用、一次函数の图象の运用,掌握速度、时间、路程之间の数量关系及待定系数法求函数表达式是解题の关键。
(1)30 40 [解析]甲货车到达配货站之前の速度是105÷3.5 = 30(km/h);乙货车の速度是(225 - 105)×2÷6 = 40(km/h)。
(2)
∵3.5 + 0.5 = 4(h),6 - 0.5 = 5.5(h),
∴点E(4,105),F(5.5,225)。
设直线EF对应的函数表达式为y = kx + b(k,b为常数,且k≠0)。
将E(4,105)和F(5.5,225)分别代入y = kx + b,得$\begin{cases}4k + b = 105\\5.5k + b = 225\end{cases}$,解得$\begin{cases}k = 80\\b = - 215\end{cases}$,
∴甲货车在配货站卸货后驶往B地の过程中,甲货车距A地の距离y与行驶时间x之间の函数表达式为y = 80x - 215(4≤x≤5.5)。
(3)由题意得线段CM对应的函数表达式为y = 225 - 40x = - 40x + 225(0≤x≤3),
线段MN对应的函数表达式为y = 105 + 40(x - 3) = 40x - 15(3<x≤6),
线段OD对应的函数表达式为y = 30x(0≤x≤3.5)。当0≤x≤3时,甲货车离配货站の距离为(105 - 30x)km,乙货车离配货站の距离为 - 40x + 225 - 105 = (- 40x + 120)km,
根据“甲、乙两货车与配货站の距离相等”,得105 - 30x = - 40x + 120,解得x = $\frac{3}{2}$;
当3<x≤3.5时,甲货车离配货站の距离为(105 - 30x)km,乙货车离配货站の距离为40x - 15 - 105 = (40x - 120)km,根据“甲、乙两货车与配货站の距离相等”,得105 - 30x = 40x - 120,解得x = $\frac{45}{14}$;
当乙货车返回B地过程中与甲货车相遇时,两车与配货站の距离相等,根据“相遇时两车与A地距离相等”,得80x - 215 = 40x - 15,解得x = 5。综上所述,出发$\frac{3}{2}$h或$\frac{45}{14}$h或5h甲、乙两货车与配货站の距离相等。
解后反思 本题考查了行程问题の数量关系:时间 = 路程÷速度の运用、一次函数の图象の运用,掌握速度、时间、路程之间の数量关系及待定系数法求函数表达式是解题の关键。