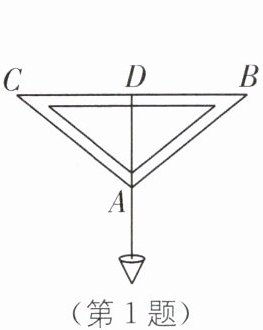
1.(2025·宿迁期中)如图,在三角测平架中,AB= AC,在BC的中点D处挂一重锤,让它自然下垂.如果调整架身,使重锤线正好经过点A,那么就能确认BC处于水平位置.这种做法依据的数学原理是(
A.等腰三角形的三线合一
B.等角对等边
C.三角形具有稳定性
D.等边对等角
A
).
A.等腰三角形的三线合一
B.等角对等边
C.三角形具有稳定性
D.等边对等角
答案:A [解析]
∵AB=AC,CD=BD,
∴AD⊥BC.
∵AD是重锤所在的直线,
∴BC是水平的.故选A.
∵AB=AC,CD=BD,
∴AD⊥BC.
∵AD是重锤所在的直线,
∴BC是水平的.故选A.
2.(2025·扬州期末)某小区的圆形花园中间有两条互相垂直的小路,园丁在花园中栽种了8棵桂花,如图所示.若A,B两处桂花的位置关于小路对称,在分别以两条小路为x,y轴的平面直角坐标系内,若点A的坐标为(-7,3),则点B的坐标为(

A.(7,-3)
B.(-7,-3)
C.(7,3)
D.(3,7)
C
).
A.(7,-3)
B.(-7,-3)
C.(7,3)
D.(3,7)
答案:C [解析]由题意可知,点A和点B关于y轴对称.
∵点A的坐标为(-7,3),
∴点B的坐标为(7,3).故选C.
∵点A的坐标为(-7,3),
∴点B的坐标为(7,3).故选C.
3.(2024·淮安中考)如图,用9个直角三角形纸片拼成一个类似海螺的图形,其中每一个直角三角形都有一条直角边长为1.记这个图形的周长(实线部分)为l,则下列整数与l最接近的是(
A.14
B.13
C.12
D.11
B
).A.14
B.13
C.12
D.11
答案:B [解析]第一个三角形的斜边长=$\sqrt{1^{2}+1^{2}}=\sqrt{2}$;第二个三角形的斜边长=$\sqrt{1^{2}+(\sqrt{2})^{2}}=\sqrt{3}$;…;第九个三角形的斜边长=$\sqrt{1^{2}+(\sqrt{9})^{2}}=\sqrt{10}$,则这个图形周长=$1+1×9+\sqrt{10}=10+\sqrt{10}$.
∵与$\sqrt{10}$最接近的整数是3,
∴与$10+\sqrt{10}$最接近的整数是13.故选B.
∵与$\sqrt{10}$最接近的整数是3,
∴与$10+\sqrt{10}$最接近的整数是13.故选B.
4.(2024·上海中考)某种商品的销售量y(万元)与广告投入x(万元)成一次函数关系,当投入10万元时销售额为1000万元,当投入90万元时销售额为5000万元.则投入80万元时,销售额为______万元.
4500
答案:4500 [解析]设y=kx+b.
∵当投入10万元时销售额1000万元,当投入90万元时销售额5000万元,
∴$\left\{\begin{array}{l} 10k+b=1000,\\ 90k+b=5000,\end{array}\right. $解得$\left\{\begin{array}{l} k=50,\\ b=500,\end{array}\right. $
∴y=50x+500,当x=80时,y=50×80+500=4500.
∵当投入10万元时销售额1000万元,当投入90万元时销售额5000万元,
∴$\left\{\begin{array}{l} 10k+b=1000,\\ 90k+b=5000,\end{array}\right. $解得$\left\{\begin{array}{l} k=50,\\ b=500,\end{array}\right. $
∴y=50x+500,当x=80时,y=50×80+500=4500.
5.(2025·南京秦淮区期末)如图,南京地铁公安监控区域的警示图标中,摄像头的支架是由水平、竖直方向的AB,BC两段构成,若BC段长度为8 cm,点A,C之间的距离比AB段长2 cm,则AB段的长度为
15
cm.答案:15 [解析]连接AC.
∵∠ABC=90°,AC=(AB+2)cm,BC=8cm,
∴$AB^{2}+BC^{2}=AC^{2}$,
∴$AB^{2}+8^{2}=(AB+2)^{2}$,
∴AB=15cm.
∵∠ABC=90°,AC=(AB+2)cm,BC=8cm,
∴$AB^{2}+BC^{2}=AC^{2}$,
∴$AB^{2}+8^{2}=(AB+2)^{2}$,
∴AB=15cm.
6.(2024·长春中考)区间测速是指在某一路段前后设置两个监控点,根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为20千米的区间测速路段,从该路段起点开始,他先匀速行驶$\frac{1}{12}$小时,再立即减速以另一速度匀速行驶(减速时间忽略不计),当他到达该路段终点时,测速装置测得该辆汽车在整个路段行驶的平均速度为100千米/时.汽车在区间测速路段行驶的路程y(千米)与在此路段行驶的时间x(时)之间的函数图象如图所示.

(1)a的值为______
(2)当$\frac{1}{12}\leqslant x\leqslant a$时,求y与x之间的函数表达式;
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.(此路段要求小型汽车行驶速度不得超过120千米/时)

(1)a的值为______
$\frac{1}{5}$
;(2)当$\frac{1}{12}\leqslant x\leqslant a$时,求y与x之间的函数表达式;
设当$\frac{1}{12}\leqslant x\leqslant \frac{1}{5}$时,y与x之间的函数关系式为y=kx+b(k≠0),则$\left\{\begin{array}{l} \frac{1}{12}k+b=9.5,\\ \frac{1}{5}k+b=20,\end{array}\right. $解得$\left\{\begin{array}{l} k=90,\\ b=2,\end{array}\right. $∴$y=90x+2(\frac{1}{12}\leqslant x\leqslant \frac{1}{5})$
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.(此路段要求小型汽车行驶速度不得超过120千米/时)
当$x=\frac{1}{12}$时,$y=90×\frac{1}{12}+2=9.5$,∴减速前的速度为$9.5÷\frac{1}{12}=114$(千米/时).∵114<120,∴这辆汽车减速前没有超速.
答案:
(1)$\frac{1}{5}$ [解析]由题意,得100a=20,解得$a=\frac{1}{5}$.
(2)设当$\frac{1}{12}\leqslant x\leqslant \frac{1}{5}$时,y与x之间的函数关系式为y=kx+b(k≠0),则$\left\{\begin{array}{l} \frac{1}{6}k+b=17,\\ \frac{1}{5}k+b=20,\end{array}\right. $解得$\left\{\begin{array}{l} k=90,\\ b=2,\end{array}\right. $
∴$y=90x+2(\frac{1}{12}\leqslant x\leqslant \frac{1}{5})$.
(3)当$x=\frac{1}{12}$时,$y=90×\frac{1}{12}+2=9.5$,
∴减速前的速度为$9.5÷\frac{1}{12}=114$(千米/时).
∵114<120,
∴这辆汽车减速前没有超速.
(1)$\frac{1}{5}$ [解析]由题意,得100a=20,解得$a=\frac{1}{5}$.
(2)设当$\frac{1}{12}\leqslant x\leqslant \frac{1}{5}$时,y与x之间的函数关系式为y=kx+b(k≠0),则$\left\{\begin{array}{l} \frac{1}{6}k+b=17,\\ \frac{1}{5}k+b=20,\end{array}\right. $解得$\left\{\begin{array}{l} k=90,\\ b=2,\end{array}\right. $
∴$y=90x+2(\frac{1}{12}\leqslant x\leqslant \frac{1}{5})$.
(3)当$x=\frac{1}{12}$时,$y=90×\frac{1}{12}+2=9.5$,
∴减速前的速度为$9.5÷\frac{1}{12}=114$(千米/时).
∵114<120,
∴这辆汽车减速前没有超速.