7.(2024·眉山中考)如图,图(1)是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图(1)中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图(2),则图(2)中大正方形的面积为( ).
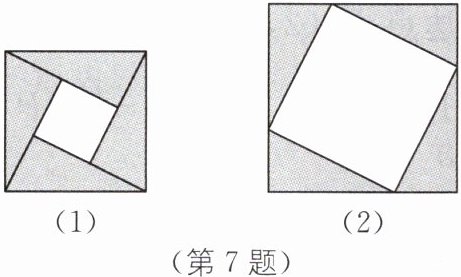
A.24
B.36
C.40
D.44
A.24
B.36
C.40
D.44
答案：
D ［解析］如图
(1)，设直角三角形的两直角边为a，b，斜边为c.
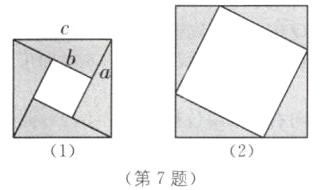
∵图
(1)中大正方形的面积是24，
∴$a^{2}+b^{2}=c^{2}=24$.
∵小正方形的面积是4，
∴$(a - b)^{2}=a^{2}+b^{2}-2ab=4$，
∴ab=10，
∴图
(2)中最大的正方形的面积为$c^{2}+4×\frac{1}{2}ab=24+2×10=44$.故选D.
D ［解析］如图
(1)，设直角三角形的两直角边为a，b，斜边为c.
∵图
(1)中大正方形的面积是24，
∴$a^{2}+b^{2}=c^{2}=24$.
∵小正方形的面积是4，
∴$(a - b)^{2}=a^{2}+b^{2}-2ab=4$，
∴ab=10，
∴图
(2)中最大的正方形的面积为$c^{2}+4×\frac{1}{2}ab=24+2×10=44$.故选D.
8.(2024·甘肃中考)敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》以表格形式将长方形土地的面积直观展示,可迅速准确地查出边长10步到60步的长方形田地面积,极大地提高了农田面积的测量效率.如图是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步,宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为(
A.一亩八十步
B.一亩二十步
C.半亩七十八步
D.半亩八十四步
B
).A.一亩八十步
B.一亩二十步
C.半亩七十八步
D.半亩八十四步
答案：B ［解析］由题图可知，小桌的长为2x尺，则y=x+x+2x，即y=4x.故选B.
归纳总结 本题考查函数表达式、图形的变化，由题图得到小桌长与宽的数量关系，从而得到长桌的长与宽的数量关系是解题的关键.
归纳总结 本题考查函数表达式、图形的变化，由题图得到小桌长与宽的数量关系，从而得到长桌的长与宽的数量关系是解题的关键.
9.(2024·甘肃中考)如图(1),“燕几”即宴几,是世界上最早的一套组合桌,由北宋进士黄伯思设计.全套“燕几”一共有七张桌子,包括两张长桌、两张中桌和三张小桌,每张桌面的宽都相等.七张桌面分开可组合成不同的图形.如图(2)给出了《燕几图》中名称为“回文”的桌面拼合方式,若设每张桌面的宽为x尺,长桌的长为y尺,则y与x的关系可以表示为(
A.$y= 3x$
B.$y= 4x$
C.$y= 3x+1$
D.$y= 4x+1$
y=2x
).A.$y= 3x$
B.$y= 4x$
C.$y= 3x+1$
D.$y= 4x+1$
答案：$x^{2}+2^{2}=(x+0.5)^{2}$ ［解析］在Rt△AB'C中，由勾股定理，得$AC^{2}+B'C^{2}=AB'^{2}$，即$x^{2}+2^{2}=(x+0.5)^{2}$.
10.(2024·吉林中考)图(1)中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图(2),其中$AB= AB'$,$AB\perp B'C$于点C,$BC= 0.5$尺,$B'C= 2$尺.设AC的长度为x尺,可列方程为
$x² + 2² = (x + 0.5)²$
.答案：解：设湖水深度AC为x尺，则红莲高度AB = AB' = (x + 0.5)尺。
在Rt△AB'C中，AC = x，B'C = 2，AB' = x + 0.5，
由勾股定理得：AC² + B'C² = AB'²，
即x² + 2² = (x + 0.5)²。
x² + 2² = (x + 0.5)²
在Rt△AB'C中，AC = x，B'C = 2，AB' = x + 0.5，
由勾股定理得：AC² + B'C² = AB'²，
即x² + 2² = (x + 0.5)²。
x² + 2² = (x + 0.5)²
11.(2024·安徽中考)我国古代数学家张衡将圆周率取值为$\sqrt{10}$,祖冲之给出圆周率的一种分数形式的近似值为$\frac{22}{7}$.比较大小：$\sqrt{10}$
＞
$\frac{22}{7}$(填“＞”或“＜”).答案：＞ ［解析］$(\sqrt{10})^{2}=10$，$(\frac{22}{7})^{2}=\frac{484}{49}$.
∵$10＞\frac{484}{49}$，
∴$\sqrt{10}＞\frac{22}{7}$.
∵$10＞\frac{484}{49}$，
∴$\sqrt{10}＞\frac{22}{7}$.